






2020-2021学年第13章 三角形中的边角关系、命题与证明13.2 命题与证明教学ppt课件
展开在证明命题时,要分清命题的条件和结论,如果问题与图形有关,首先画出图形,再结合图形,写出已知、求证.
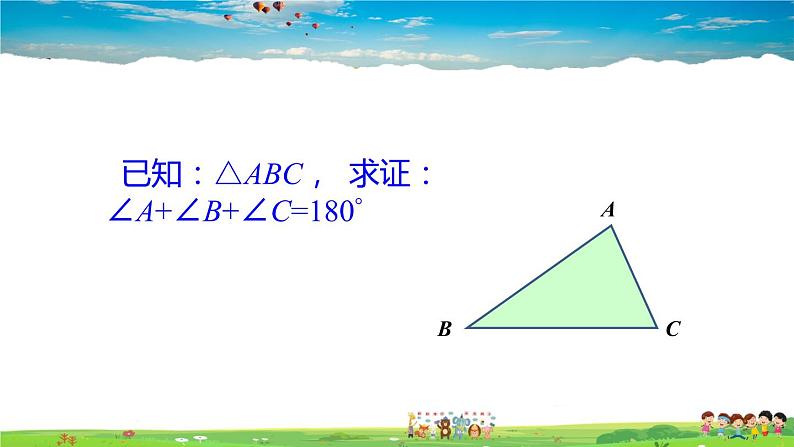
命题:三角形的内角和等于180°.
已知:△ABC, 求证:∠A+∠B+∠C=180°
分析:以前我们通过剪拼将三角形的三个内角拼成了一个平角,这不是证明,但它却给我们以启发.现在我们通过作图来实现这种转化,给出证明.
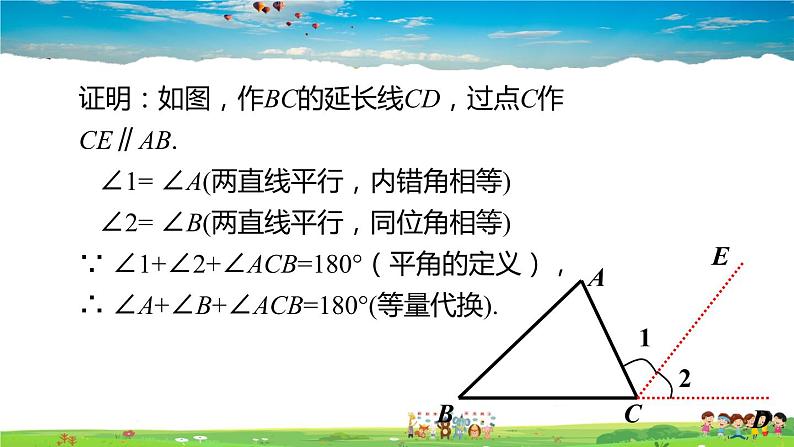
证明:如图,作BC的延长线CD,过点C作CE∥AB. ∠1= ∠A(两直线平行,内错角相等) ∠2= ∠B(两直线平行,同位角相等)∵ ∠1+∠2+∠ACB=180°(平角的定义),∴ ∠A+∠B+∠ACB=180°(等量代换).
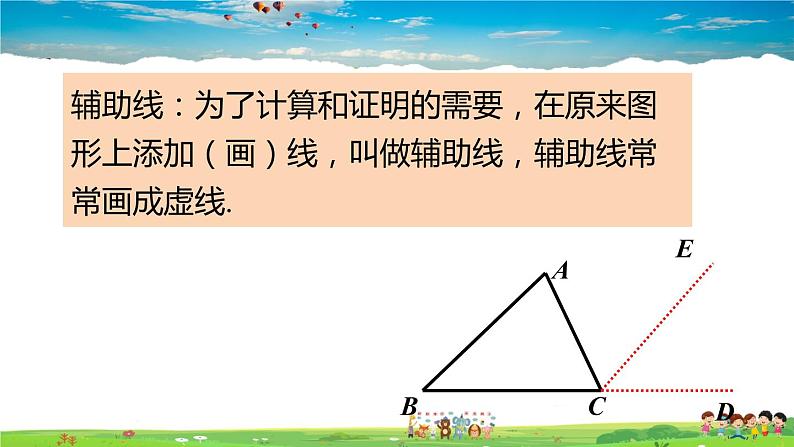
辅助线:为了计算和证明的需要,在原来图形上添加(画)线,叫做辅助线,辅助线常常画成虚线.
直角三角形中的两个锐角之间有着怎样的关系?请用几何语言证明.
根据三角形内角和定理,另两个角的和应该为90°,于是得
推论1 直角三角形的两锐角互余.
像这样,由基本事实、定理直接得出的真命题叫做推论.
推论2 有两个角互余的三角形是直角三角形.
补充完成下列证明,并填上推理的依据: 已知:如图,△ABC. 求证:∠A+∠B+∠C=180°.
证明 过点A作DE//BC,则 ∠DAB= ,( ) ∠EAC= ,( )∵ ∠DAB+∠BAC+∠EAC= ,(所作)∴ ∠B+∠BAC+∠C= + + ( ) =180°.
2. 补充完成下列证明: 已知:如图,△ABC. 求证:∠A+∠B+∠C=180°. 证明 D是BC边上一点,过点D作 DE//AB,DF//AC,分别交AC,AB于 点E,F.∵ DE//AB,(所作)
∴∠A=∠4 ∠B=∠3又∵DF//AC∴∠C=∠1 ∠2=∠4∴∠A=∠2又∵∠1+∠2+∠3=180°
∴∠A+∠B+∠C=180°
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
△ABC的外角∠ACD与它不相邻的内角∠ A、 ∠ B有怎样的关系?
证明: △ABC中∵∠A+∠B+∠ACB=180°(三角形内角和定理)∠ACB+∠ACD=180°(平角定义)∴∠ACD=∠A+∠B(等量代换)
推论3 三角形的一个外角等于与它不相邻 的两个内角的和.推论4 三角形的一个外角大于与它不相邻 的任何一个内角.
已知:如图,∠1、∠2、∠3是 △ABC的三个外角 求证: ∠1+∠2+∠3=360°
证明 ∵∠1=∠ABC+∠ACB ∠2=∠BAC+∠ACB ∠3=∠BAC+∠ABC,(三角形的一个外角等于与它不相邻的两个内角的和) ∴ ∠1+∠2+∠3=2(∠ABC+∠ACB+∠BAC).(等式性质)∵∠ABC+∠ACB+∠BAC=180°,(三角形内角和定理)∴∠1+∠2+∠3=360°.
填空:(1)如图,∠ABC= ,∠1= ;(2)在直角三角形中,与直角相邻的外角的度数是 .
数学八年级上册13.2 命题与证明习题ppt课件: 这是一份数学八年级上册13.2 命题与证明习题ppt课件,共24页。PPT课件主要包含了辅助线,直角三角形,°或60°,等量代换等内容,欢迎下载使用。
沪科版八年级上册13.2 命题与证明图片课件ppt: 这是一份沪科版八年级上册13.2 命题与证明图片课件ppt,共23页。PPT课件主要包含了学习目标,导入新课,情境引入,讲授新课,已知△ABC,知识要点,思路总结,作辅助线,基本图形,总结归纳等内容,欢迎下载使用。
初中数学沪科版八年级上册13.2 命题与证明授课ppt课件: 这是一份初中数学沪科版八年级上册13.2 命题与证明授课ppt课件,共56页。PPT课件主要包含了那么这个数是偶数,如果一个数能被2整除,那么这两个角是对顶角,如果两个角有公共顶点,那么它们的同位角相等,如果两条直线平行,那么这两条直线平行,如果两个同位角相等,不是命题,是命题等内容,欢迎下载使用。













