初中数学浙教版八年级上册1.3 证明课后测评

这是一份初中数学浙教版八年级上册1.3 证明课后测评，共18页。

A．100°B．120°C．130°D．140°
2．（2021春•保山期末）如图，在△ABC中，CD是角平分线，∠A＝30°，∠CDB＝65°，则∠B的度数为（ ）
A．65°B．70°C．80°D．85°
3．（2019秋•鄂城区期中）如图，△ABC的外角∠CAE为115°，∠C＝80°，则∠B的余角为（ ）
A．55°B．45°C．35°D．30°
4．（2020春•长安区校级期末）如图，∠ABC＝∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF；则以下结论：①AD∥BC；②∠ACB＝2∠ADB；③∠ADC+∠ABD＝90°；其中正确的结论有（ ）
A．0个B．1个C．2个D．3个
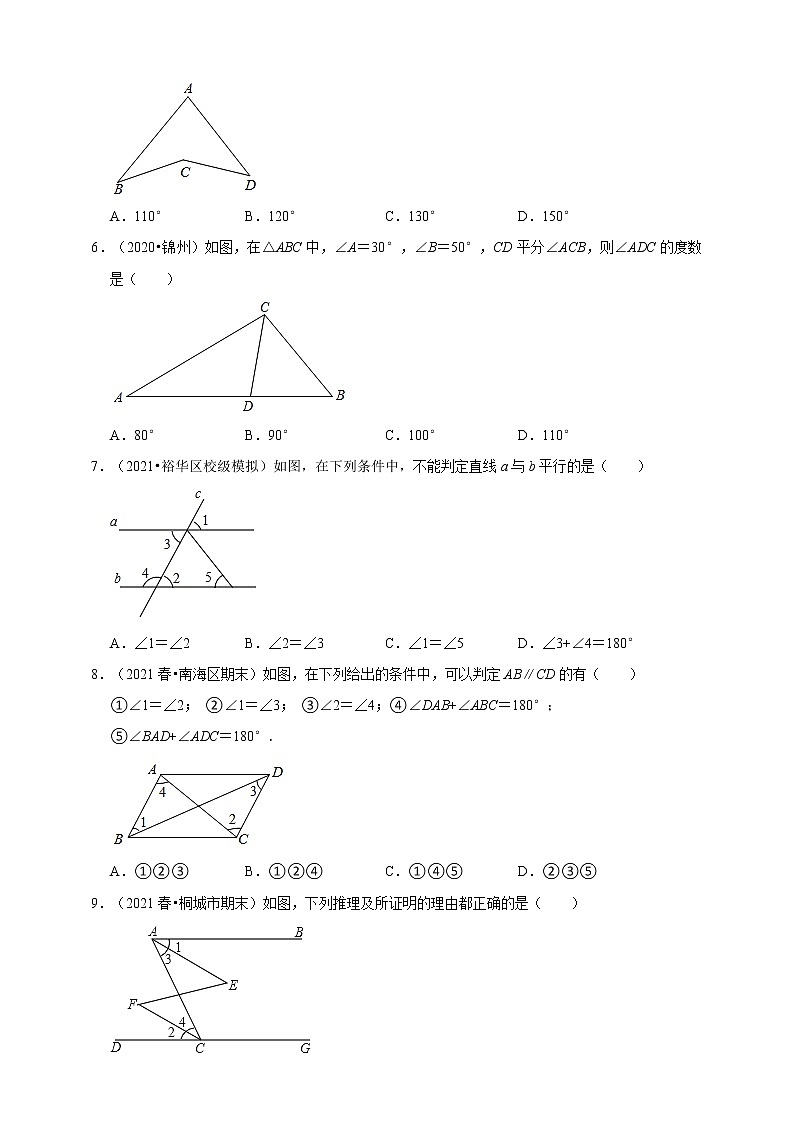
5．（2021春•工业园区校级月考）如图，点C是∠BAD内一点，连CB、CD，∠A＝80°，∠B＝10°，∠D＝40°，则∠BCD的度数是（ ）
A．110°B．120°C．130°D．150°
6．（2020•锦州）如图，在△ABC中，∠A＝30°，∠B＝50°，CD平分∠ACB，则∠ADC的度数是（ ）
A．80°B．90°C．100°D．110°
7．（2021•裕华区校级模拟）如图，在下列条件中，不能判定直线a与b平行的是（ ）
A．∠1＝∠2B．∠2＝∠3C．∠1＝∠5D．∠3+∠4＝180°
8．（2021春•南海区期末）如图，在下列给出的条件中，可以判定AB∥CD的有（ ）
①∠1＝∠2； ②∠1＝∠3； ③∠2＝∠4；④∠DAB+∠ABC＝180°；
⑤∠BAD+∠ADC＝180°．
A．①②③B．①②④C．①④⑤D．②③⑤
9．（2021春•桐城市期末）如图，下列推理及所证明的理由都正确的是（ ）
A．若AB∥DG，则∠BAC＝∠DCA，理由是内错角相等，两直线平行
B．若AB∥DG，则∠3＝∠4，理由是两直线平行，内错角相等
C．若AE∥CF，则∠E＝∠F，理由是内错角相等，两直线平行
D．若AE∥CF，则∠3＝∠4，理由是两直线平行，内错角相等
10．（2021春•姑苏区期中）如图，在△ABC中，AE平分∠BAC，AD⊥BC于点D．∠ABD的角平分线BF所在直线与射线AE相交于点G，若∠ABC＝3∠C，且∠G＝20°，则∠DFB的度数为（ ）
A．50°B．55°C．60°D．65°
二．填空题
11．（2020秋•罗湖区期末）如图，已知△ABC中，∠A＝50°，BE平分∠ABC，CE平分外角∠ACD，则∠E＝ 度．
12．（2021春•道里区期末）如图，在△ABC中，AD平分∠BAC与BC相交于点D，若∠B＝42°，∠BAD＝28°，则∠C的度数是 度．
13．（2021春•会宁县期末）一个零件的形状如图所示，按规定∠A等于90°，∠B，∠D应分别是20°和30°，聪明的李叔叔通过量得∠BCD的度数就断定这个零件是否合格，那么∠BCD＝ 时这个零件合格．
14．（2021春•阳谷县期末）如图，木工用角尺画出CD∥EF，其依据是 ．
15．（2020秋•鼓楼区校级期末）将一副三角板如图所示摆放，若∠BAE＝125°，则∠CAD的度数是 ．
16．（2021春•姑苏区期末）如图，在△ABC中，∠BAC＝100°，AD⊥BC于D点，AE平分∠BAC交BC于点E．若∠C＝26°，则∠DAE的度数为 ．
三．解答题
17．在横线上填上适当的内容，完成下面的证明．
已知，直线a，b，c，d的位置如图所示，∠1+∠2＝180°，∠3＝∠4，∠求证：c∥d．
证明：如图，
∵∠2+∠3＝180°（ ），
∠1+∠2＝180° （ ），
∴ ＝ （同角的补角相等），
又∵∠3＝∠4（已知），
∴∠1＝∠4 （ ），
∴ ∥ （ ）．
18．（2021春•泰州期末）如图1，D为△ABC的边BC上一点，若∠ADC＝∠BAC，
（1）求证：∠DAC＝∠B；
（2）如图2，若AE平分∠BAD，在图中找出与∠EAC相等的角，并加以证明．
19．（2020秋•兰州期末）已知：如图，直线BD分别交射线AE、CF于点B、D，连接AD和BC、∠1+∠2＝180°，∠A＝∠C，求证：AD∥BC．
20．（2021春•海淀区校级期末）如图，在△ABC中，AD⊥BC，EF⊥BC，∠1＝∠2．试说明：DG∥BA．
21．（2021春•无为市月考）如图，∠1+∠2＝180°，∠3＝∠B．求证：DE∥BC．
22．（2021春•甘井子区期末）如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E．
求证：∠BAC＝∠B+2∠E．
23．如图，∠BAF，∠CBD与∠ACE是△ABC的三个外角．你能求出这三个外角度数之和吗？说明你的理由．
答案与解析
一．选择题
1．（2020秋•鼓楼区校级期末）如图，∠1＝140°，∠2＝100°，则∠3＝（ ）
A．100°B．120°C．130°D．140°
【解答】解：∵∠1＝140°，∠2＝100°，
∴∠3＝360°﹣140°﹣100°＝120°，
故选：B．
2．（2021春•保山期末）如图，在△ABC中，CD是角平分线，∠A＝30°，∠CDB＝65°，则∠B的度数为（ ）
A．65°B．70°C．80°D．85°
【解答】解：∵CD平分∠ACB，
∴∠ACB＝2∠ACD．
∵∠CDB＝∠A+∠ACD，
∴∠ACD＝∠CDB﹣∠A＝65°﹣30°＝35°．
∴∠ACB＝2∠ACD＝70°．
∴∠B＝180°﹣（∠A+∠ACB）＝80°．
故选：C．
3．（2019秋•鄂城区期中）如图，△ABC的外角∠CAE为115°，∠C＝80°，则∠B的余角为（ ）
A．55°B．45°C．35°D．30°
【解答】解：∠B＝∠CAE﹣∠C＝35°，
∴∠B的余角＝90°﹣35°＝55°，
故选：A．
4．（2020春•长安区校级期末）如图，∠ABC＝∠ACB，AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF；则以下结论：①AD∥BC；②∠ACB＝2∠ADB；③∠ADC+∠ABD＝90°；其中正确的结论有（ ）
A．0个B．1个C．2个D．3个
【解答】解：AD平分∠EAC，
∴∠EAC＝2∠EAD＝2∠CAD，
∵∠ABC＝∠ACB，∠EAC＝∠ABC+∠ACB，
∴∠EAC＝2∠ABC，
∴∠EAD＝∠ABC，
∴AD∥BC，故①正确；
∴∠ADB＝∠DBC，
∵BD平分∠ABC，
∴∠ABC＝2∠DBC＝2∠ADB，
∴∠ACB＝2∠ADB，故②正确；
∵AD∥BC，
∴∠ADC＝∠DCF，
∵CD平分∠ACF，
∴∠ACF＝2∠DCF，
∵∠ACB+∠ACF＝180°，∠ACB＝∠ABC＝2∠ABD，
∴2∠ABD+2∠ADC＝180°，
∴∠ABD+∠ADC＝90°，故③正确，
故选：D．
5．（2021春•工业园区校级月考）如图，点C是∠BAD内一点，连CB、CD，∠A＝80°，∠B＝10°，∠D＝40°，则∠BCD的度数是（ ）
A．110°B．120°C．130°D．150°
【解答】解：延长BC交AD于E，
∵∠BED是△ABE的一个外角，∠A＝80°，∠B＝10°，
∴∠BED＝∠A+∠B＝90°，
∵∠BCD是△CDE的一个外角
∴∠BCD＝∠BED+∠D＝130°，
故选：C．
6．（2020•锦州）如图，在△ABC中，∠A＝30°，∠B＝50°，CD平分∠ACB，则∠ADC的度数是（ ）
A．80°B．90°C．100°D．110°
【解答】解：∵∠A＝30°，∠B＝50°，
∴∠ACB＝180°﹣30°﹣50°＝100°（三角形内角和定义）．
∵CD平分∠ACB，
∴∠BCD＝∠ACB＝×100°＝50°，
∴∠ADC＝∠BCD+∠B＝50°+50°＝100°．
故选：C．
7．（2021•裕华区校级模拟）如图，在下列条件中，不能判定直线a与b平行的是（ ）
A．∠1＝∠2B．∠2＝∠3C．∠1＝∠5D．∠3+∠4＝180°
【解答】解：A、∵∠1＝∠2，∴a∥b，不符合题意；
B、∵∠2＝∠3，∴a∥b，不符合题意；
C、∵∠1与∠5既不是直线a，b被任何一条直线所截的一组同位角，内错角，
∴∠1＝∠5，不能得到a∥b，
∴符合题意；
D、∵∠3+∠4＝180°，∴a∥b，不符合题意；
故选：C．
8．（2021春•南海区期末）如图，在下列给出的条件中，可以判定AB∥CD的有（ ）
①∠1＝∠2；②∠1＝∠3；③∠2＝∠4；④∠DAB+∠ABC＝180°；⑤∠BAD+∠ADC＝180°．
A．①②③B．①②④C．①④⑤D．②③⑤
【解答】解：①∠1＝∠2不能判定AB∥CD，不符合题意；
②∵∠1＝∠3，∴AB∥CD，符合题意；
③∵∠2＝∠4，∴AB∥CD，符合题意；
④∠DAB+∠ABC＝180°；不能判定AB∥CD，不符合题意；
⑤∵∠BAD+∠ADC＝180°，∴AB∥CD，符合题意．
故选：D．
9．（2021春•桐城市期末）如图，下列推理及所证明的理由都正确的是（ ）
A．若AB∥DG，则∠BAC＝∠DCA，理由是内错角相等，两直线平行
B．若AB∥DG，则∠3＝∠4，理由是两直线平行，内错角相等
C．若AE∥CF，则∠E＝∠F，理由是内错角相等，两直线平行
D．若AE∥CF，则∠3＝∠4，理由是两直线平行，内错角相等
【解答】解：A、若AB∥DG，则∠BAC＝∠DCA，理由是两直线平行，内错角相等；故选项A错误；
B、若AB∥DG，则∠BAC＝∠DCA，并不是∠3＝∠4，理由是两直线平行，内错角相等；故选项B错误；
C、若AE∥CF，则∠E＝∠F，理由是两直线平行，内错角相等；故选项C错误；
D、若AE∥CF，则∠3＝∠4，理由是两直线平行，内错角相等；正确；
故选：D．
10．（2021春•姑苏区期中）如图，在△ABC中，AE平分∠BAC，AD⊥BC于点D．∠ABD的角平分线BF所在直线与射线AE相交于点G，若∠ABC＝3∠C，且∠G＝20°，则∠DFB的度数为（ ）
A．50°B．55°C．60°D．65°
【解答】解：如图：
∵AE平分∠BAC，BF平分∠ABD，
∴∠CAE＝∠BAE，∠1＝∠2，
设∠CAE＝∠BAE＝x，∠C＝y，∠ABC＝3y，
由外角的性质得：
∠1＝∠BAE+∠G＝x+20，∠2＝∠ABD＝（2x+y）＝x+y，
∴x+20＝x+y，解得y＝40°，
∴∠1＝∠2＝（180°﹣∠ABC）＝×（180°﹣120°）＝30°，
∴∠DFB＝60°．
故选：C．
二．填空题
11．（2020秋•罗湖区期末）如图，已知△ABC中，∠A＝50°，BE平分∠ABC，CE平分外角∠ACD，则∠E＝ 25 度．
【解答】解：∵BE平分∠ABC，CE平分∠ACD，
∴∠ABC＝2∠EBC，∠ACD＝2∠DCE，
∵∠ACD＝2∠DCE＝∠A+∠ABC，∠DCE＝∠E+∠EBC，
∴2∠DCE＝2∠E+2∠EBC，
∴∠ACD＝2∠E+∠ABC，
∴2∠E+∠ABC＝∠A+∠ABC，
∴∠A＝2∠E，
∵∠A＝50°，
∴∠E＝25°，
故答案为：25．
12．（2021春•道里区期末）如图，在△ABC中，AD平分∠BAC与BC相交于点D，若∠B＝42°，∠BAD＝28°，则∠C的度数是 82 度．
【解答】解：∵AD平分∠BAC，∠BAD＝28°，
∴∠BAC＝2∠BAD＝56°，
∴∠C＝180°﹣∠B﹣∠BAC＝82°，
故答案为：82．
13．（2021春•会宁县期末）一个零件的形状如图所示，按规定∠A等于90°，∠B，∠D应分别是20°和30°，聪明的李叔叔通过量得∠BCD的度数就断定这个零件是否合格，那么∠BCD＝ 140° 时这个零件合格．
【解答】解：延长DC交AB于E，
∠BCD＝∠B+∠CEB
＝∠B+∠D+∠A
＝20°+30°+90°
＝140°，
故答案为：140°．
14．（2021春•阳谷县期末）如图，木工用角尺画出CD∥EF，其依据是 同位角相等，两直线平行 ．
【解答】解：木工用角尺画出CD∥EF，其依据是同位角相等，两直线平行，
故答案为：同位角相等，两直线平行．
15．（2020秋•鼓楼区校级期末）将一副三角板如图所示摆放，若∠BAE＝125°，则∠CAD的度数是 55° ．
【解答】解：∵∠BAE＝125°，
∴∠DAE＝∠BAE﹣∠BAD＝125°﹣90°＝35°，
∴∠CAD＝∠CAE﹣∠DAE＝90°﹣35°＝55°，
故答案为：55°．
16．（2021春•姑苏区期末）如图，在△ABC中，∠BAC＝100°，AD⊥BC于D点，AE平分∠BAC交BC于点E．若∠C＝26°，则∠DAE的度数为 14° ．
【解答】解：∵AD⊥BC，
∴∠ADC＝90°，
∴∠CAD＝180°﹣∠ADC﹣∠C＝180°﹣90°﹣26°＝64°，
∵AE平分∠BAC，
∴∠CAE＝∠BAC＝×100°＝50°，
∴∠DAE＝∠CAD﹣∠CAE＝64°﹣50°＝14°．
故答案为14°．
三．解答题
17．在横线上填上适当的内容，完成下面的证明．
已知，直线a，b，c，d的位置如图所示，∠1+∠2＝180°，∠3＝∠4，∠求证：c∥d．
证明：如图，
∵∠2+∠3＝180°（ 邻补角的定义 ），
∠1+∠2＝180° （ 已知 ），
∴ ∠3 ＝ ∠1 （同角的补角相等），
又∵∠3＝∠4（已知），
∴∠1＝∠4 （ 等量代换 ），
∴ c ∥ d （ 内错角相等，两直线平行 ）．
【解答】证明：如图，
∵∠2+∠3＝180°（邻补角的定义），
∠1+∠2＝180° （已知），
∴∠3＝∠1（同角的补角相等），
又∵∠3＝∠4（已知），
∴∠1＝∠4 （等量代换），
∴c∥d（内错角相等，两直线平行）．
故答案为：邻补角的定义；已知；∠3；∠1；等量代换；c；d；内错角相等，两直线平行．
18．（2021春•泰州期末）如图1，D为△ABC的边BC上一点，若∠ADC＝∠BAC，
（1）求证：∠DAC＝∠B；
（2）如图2，若AE平分∠BAD，在图中找出与∠EAC相等的角，并加以证明．
【解答】（1）证明：∵∠ADC是△ABD的外角，
∴∠ADC＝∠BAD+∠B，
∵∠BAC＝∠BAD+∠DAC，∠ADC＝∠BAC，
∴∠DAC＝∠B；
（2）解：∠EAC＝∠AEC，
理由如下：∵∠AEC是△ABE的外角，
∴∠AEC＝∠BAE+∠B，
∵AE平分∠BAD，
∴∠BAE＝∠EAD，
由（1）可知：∠DAC＝∠B，
∴∠EAC＝∠AEC．
19．（2020秋•兰州期末）已知：如图，直线BD分别交射线AE、CF于点B、D，连接AD和BC、∠1+∠2＝180°，∠A＝∠C，求证：AD∥BC．
【解答】证明：∠2+∠BDC＝180°，∠1+∠2＝180°，
∴∠1＝∠BDC，
∴AB∥CF，
∴∠C＝∠EBC，
∵∠A＝∠C，
∴∠A＝∠EBC，
∴AD∥BC．
20．（2021春•海淀区校级期末）如图，在△ABC中，AD⊥BC，EF⊥BC，∠1＝∠2．试说明：DG∥BA．
【解答】证明：∵AD⊥BC，EF⊥BC，
∴∠EFB＝∠ADB＝90°，
∴EF∥AD，
∴∠1＝∠BAD，
又∵∠1＝∠2，
∴∠2＝∠BAD，
∴DG∥AB．
21．（2021春•无为市月考）如图，∠1+∠2＝180°，∠3＝∠B．求证：DE∥BC．
【解答】证明：∵∠1+∠2＝180°（已知），∠2+∠ADC＝180°（平角定义），
∴∠1＝∠ADC，
∴EF∥AB（同位角相等，两直线平行），
∴∠3＝∠ADE（两直线平行，内错角相等），
又∵∠3＝∠B（已知），
∴∠ADE＝∠B，
∴DE∥BC（同位角相等，两直线平行）．
22．（2021春•甘井子区期末）如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E．
求证：∠BAC＝∠B+2∠E．
【解答】证明：∵CE平分∠ACD，
∴∠ACE＝∠ACD．
∵∠CAB＝∠E+∠ACE，
∴∠CAB＝∠E+．
∵∠ACD＝∠B+∠CAB，
∴∠CAB＝∠E+．
∴2∠CAB＝2∠E+∠B+∠CAB．
∴∠CAB＝∠B+2∠E．
23．如图，∠BAF，∠CBD与∠ACE是△ABC的三个外角．你能求出这三个外角度数之和吗？说明你的理由．
【解答】解：∵∠BAF+∠BAC＝180°，∠CBD+∠ABC＝180°，∠ACE+∠ACB＝180°，
∴∠BAF+∠BAC+∠CBD+∠ABC+∠ACE+∠ACB＝3×180°＝540°，
∵∠BAC+∠ABC+∠ACB＝180°，
∴∠BAF+∠CBD+∠ACE＝540°﹣180°＝360°，
即三个外角的和等于360°．