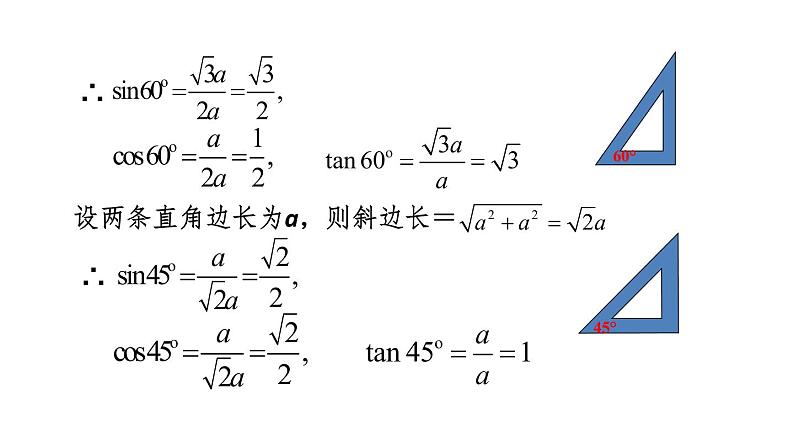
2021学年28.1 锐角三角函数课前预习课件ppt

这是一份2021学年28.1 锐角三角函数课前预习课件ppt，共36页。PPT课件主要包含了学习目标，导入新知，另一条直角边长＝，合作探究，三角函数，解1原式，2原式，＝1-1，巩固新知，∴α60°等内容，欢迎下载使用。

1.理解特殊角的三角函数值的由来。2.运用三角函数的知识，自主探索，推导出30°、45°、60°角的三角函数值。3.熟记三个特殊锐角的三角函数值，并能准确地加以运用，根据一个特殊角的三角函数值说出这个角。
设30°所对的直角边长为a，那么斜边长为2a，
新知 特殊角（30°、45°、60°）的三角函数值
设两条直角边长为a，则斜边长＝
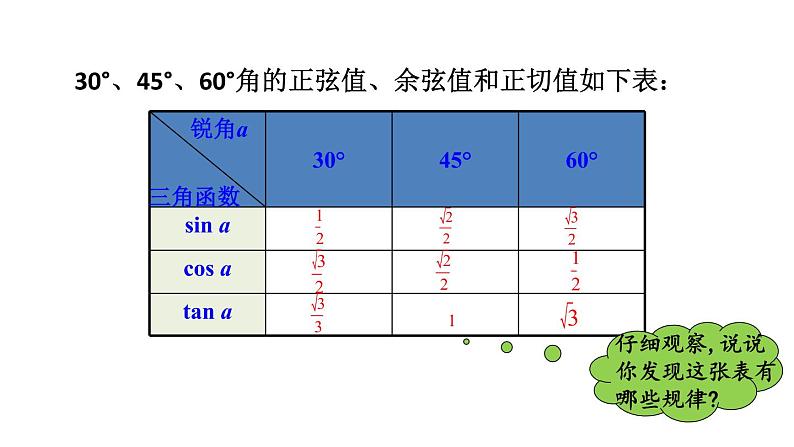
30°、45°、60°角的正弦值、余弦值和正切值如下表：
解： （1） cs260°＋sin260°
典例精析1 特殊角的三角函数值的运算
提示：sin260°表示（sin60°）2
含特殊角三角函数值的计算注意事项：（1）熟记特殊角的锐角三角函数值是关键；（2）注意运算顺序和法则；（3）注意特殊角三角函数值的准确代入．
1.计算：(1) sin30°+ cs45°；
(2) sin230°+ cs230°－tan45°.
解：在 Rt△ABC中
∴ ∠A = 45°.
典例精析2 利用三角函数值求特殊角
解：在 Rt△ABO中
2. 在Rt△ABC中，∠C＝90°， 求∠A、∠B的度数．
∠B = 90°－ ∠ A = 90°－30°= 60°
∴ tanA＝1， ， ∠C＝180°－45°－60°＝75°， ∴ △ABC 是锐角三角形．
典例精析3 特殊角的三角函数值的应用
∴ ∠A＝45°，∠B＝60°，
3. 已知：求∠A，∠B的度数。
4．如图，网格中的四个格点组成了菱形ABCD，则tan ∠DBC的值为____．
8．计算：sin230°－tan60°－sin245°＋cs230°
11．在Rt△ABC中，∠C＝90°，∠B＝52°，c＝14，解直角三角形．(结果精确到0.1，参考数据：sin52°≈0.788 0，cs52°≈0.615 7，tan52°≈1.279 9)解：∠A＝90°－∠B＝90°－52°＝38°，AC＝c·sin B＝14×sin 52°≈14×0.788 0≈11.0，BC＝c·cs 52°≈14×0.615 7≈8.6
12．如图，在△ABC中，∠ABC＝90°，∠A＝30°，D是边AB上一边，∠BDC＝45°，AD＝4，求BC的长．(结果保留根号)
1．(衢州中考)如图，人字梯AB，AC的长都为2米，当α＝50°时，人字梯顶端离地面的高度AD是_______米(结果精确到0.1 m．参考数据：sin50°≈0.77，cs50°≈0.64，tan 50°≈1.19).
2．如图，某公园入口处原有三级台阶，每级台阶高为18 cm，深为30 cm，为方便残疾人士，拟将台阶改为斜坡，设台阶的起始点为A，斜坡的起始点为C，现设计斜坡BC的坡度i＝1∶5，则AC的长度是________cm.
3．(内江中考)为了维护我国海洋权力，海监部门对我国领海实行了常态化巡航管理．如图，正在执行巡航任务的海监船以每小时60海里的速度向正东方向航行，在A处测得灯塔P在北偏东60°方向上，海监船继续向东航行1小时到达B处，此时测得灯塔P在北偏东30°方向上．(1)求B处到灯塔P的距离；(2)已知灯塔P的周围50海里内有暗礁，若海监船继续向正东方向航行是否安全？
4．(聊城中考)如图，小莹在数学综合实践活动中，利用所学的数学知识对某小区居民楼AB的高度进行测量，先测得居民楼AB与CD之间的距离AC为35 m，后站在M点处测得居民楼CD的顶端D的仰角为45°，居民楼AB的顶端B的仰角为55°，已知居民楼CD的高度为16.6 m，小莹的观测点N距地面1.6 m．求居民楼AB的高度(精确到1 m).(参考数据：sin55°≈0.82，cs55°≈0.57，tan55°≈1.43).
5．【实践探究】(武威中考)图①是甘肃省博物馆的镇馆之宝——铜奔马，又称“马踏飞燕”，于1969年10月出土于武威市的雷台汉墓，1983年10月被国家旅游局确定为中国旅游标志．在很多旅游城市的广场上都有“马踏飞燕”雕塑．某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动，同学们制定了测量方案，并完成了实地测量，测得结果如下表：
请你根据上表中的测量数据，帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据：sin31°≈0.52，cs31°≈0.86，tan31°≈0.60，sin42°≈0.67，cs42°≈0.74，tan42°≈0.90)