2019-2020学年河北省邯郸市大名县九年级（上）期中数学试卷（冀教版）

这是一份2019-2020学年河北省邯郸市大名县九年级（上）期中数学试卷（冀教版），共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 下列是一元二次方程的是（ ）
A.x2+3x−1＝0B.3x2+x+3C.1x+x=1D.4x+1＝0

2. 关于一组数据：1，5，6，3，5，下列说法错误的是（ ）
A.平均数是4B.众数是5C.中位数是6D.方差是3.2

3. 如图，AF // BE // CD，且AB＝1，BC＝2.5，ED＝3，则FE的长度为（ ）

A.2B.1C.1.2D.1.5

4. 如图，AB与CD相交于点E，AD // BC，BEAE=35，CD＝16，则DE的长为（ ）

A.3B.6C.485D.10

5. 已知Rt△ABC中，∠C＝90∘，AC＝4，BC＝6，那么下列各式中，正确的是（ ）
A.sinA=23B.csA=23C.tanA=23D.tanB=23

6. 反比例函数y=−6x的图象位于（ ）
A.第一、二象限B.第三、四象限C.第一、三象限D.第二、四象限

7. 某科普小组有5名成员，身高分别为（单位：cm）：160，165，170，163，167．增加1名身高为165cm的成员后，现科普小组成员的身高与原来相比，下列说法正确的是( )
A.平均数不变，方差不变B.平均数不变，方差变大
C.平均数不变，方差变小D.平均数变小，方差不变

8. 一元二次方程x2−10x+21＝0的两根恰好是等腰三角形的底边长和腰长，则该等腰三角形的周长为（ ）
A.13B.17C.13或17D.不能确定

9. 如图，在矩形ABCD中，AB＝2，BC＝3，点E是AD的中点，CF⊥BE于点F，则CF等于（ ）

A.2B.2.4C.2.5

10. 在Rt△ABC中，∠C=90∘，sinA=45，则csB的值等于( )
A.35B.45C.34D.55

11. 如图，已知点A在反比例函数y=kx(x>0)的图象上，作Rt△ABC，边BC在x轴上，点D为斜边AC的中点，连结DB并延长交y轴于点E，若△BCE的面积为4，则k的值是（ ）

A.2B.4C.6D.8

12. 如图，直角三角形纸片的两直角边长分别为6、8，按如图那样折叠，使点A与点B重合，折痕为DE，则S△BCE:S△BDE等于（ ）

A.2:5B.14:25C.16:25D.4:21

13. 如图，在Rt△ABC中，∠ABC＝90∘，AB＝6，BC＝8，点E是△ABC的内心，过点E作EF // AB交AC于点F，则EF的长为（ ）

A.52B.154C.83D.103

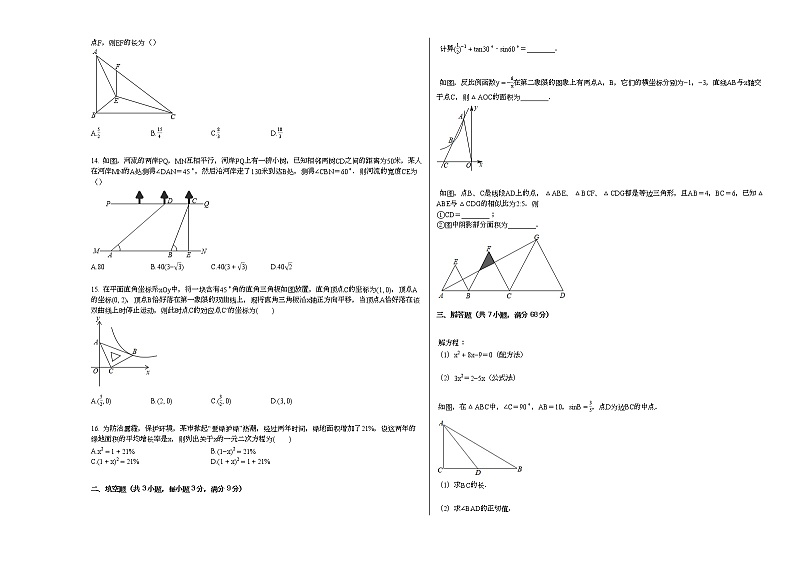
14. 如图，河流的两岸PQ，MN互相平行，河岸PQ上有一排小树，已知相邻两树CD之间的距离为50米，某人在河岸MN的A处测得∠DAN＝45∘，然后沿河岸走了130米到达B处，测得∠CBN＝60∘．则河流的宽度CE为（ ）

A.80B.40(3−3)C.40(3+3)D.402

15. 在平面直角坐标系xOy中，将一块含有45∘角的直角三角板如图放置，直角顶点C的坐标为(1, 0)，顶点A的坐标(0, 2)，顶点B恰好落在第一象限的双曲线上，现将直角三角板沿x轴正方向平移，当顶点A恰好落在该双曲线上时停止运动，则此时点C的对应点C′的坐标为( )

A.(52, 0)B.(2, 0)C.(32, 0)D.(3, 0)

16. 为防治雾霾，保护环境，某市掀起“爱绿护绿”热潮，经过两年时间，绿地面积增加了21%，设这两年的绿地面积的平均增长率是x，则列出关于x的一元二次方程为( )
A.x2=1+21%B.(1−x)2=21%
C.(1+x)2=21%D.(1+x)2=1+21%
二、填空题（共3小题，每小题3分，满分9分）

计算(12)−1+tan30∘⋅sin60∘＝________．

如图，反比例函数y=−6x在第二象限的图象上有两点A，B，它们的横坐标分别为−1，−3，直线AB与x轴交于点C，则△AOC的面积为________．


如图，点B、C是线段AD上的点，△ABE、△BCF、△CDG都是等边三角形，且AB＝4，BC＝6，已知△ABE与△CDG的相似比为2:5．则
①CD＝________；
②图中阴影部分面积为________．

三、解答题（共7小题，满分68分）

解方程：
（1）x2+8x−9＝0（配方法）

（2）3x2＝2−5x（公式法）

如图，在△ABC中，∠C＝90∘，AB＝10，sinB=35，点D为边BC的中点．

（1）求BC的长．

（2）求∠BAD的正切值．

为了解某校九年级学生的理化实验操作情况，随机抽查了40名同学实验操作的得分．根据获取的样本数据，制作了如下的条形统计图和扇形统计图．请根据相关信息，解答下列问题：
(Ⅰ)扇形 ①的圆心角的大小是________；
(Ⅱ)求这40个样本数据的平均数、众数、中位数；
(Ⅲ)若该校九年级共有320名学生，估计该校理化实验操作得满分有多少人．

如图，在△ABC中，AB=AC，点P，D分别是BC，AC边上的点，且∠APD=∠B．
(1)求证：AC⋅CD=CP⋅BP；

(2)若AB=10，BC=12，当PD // AB时，求BP的长．

如图，在△ABC中，∠B＝90∘，AB＝6厘米，BC＝8厘米．点P从A点开始沿AB边向点B以1厘米/秒的速度移动（到达点B即停止运动），点Q从B点开始沿BC边向点C以2厘米/秒的速度移动（到达点C即停止运动）．

（1）如果P、Q分别从A、B两点同时出发，经过几秒钟，△PBQ的面积等于△ABC的三分之一？

（2）如果P、Q两点分别从A、B两点同时出发，而且动点P从A点出发，沿AB移动（到达点B即停止运动），动点Q从B出发，沿BC移动（到达点C即停止运动），几秒钟后，P、Q相距6厘米？

为积极响应新旧动能转换，提高公司经济效益，某科技公司近期研发出一种新型高科技设备，每台设备的成本价为30万元，经过市场调研发现，每台售价为40万元时，年销售量为600台；每台售价为45万元时，年销售量为550台．假定该设备的年销售量y（单位：台）和销售单价x（单位：万元）成一次函数关系．
(1)求年销售量y与销售单价x的函数关系式；

(2)根据相关规定，此设备的销售单价不得高于70万元，如果该公司想获得10000万元的年利润，则该设备的销售单价应是多少万元？

如图，一次函数y＝kx+b分别交y轴、x轴于C、D两点，与反比例函数y=8x(x>0)的图象交于A(m, 8)，B(4, n)两点．

（1）求一次函数的解析式；

（2）根据图象直接写出kx+b−8x0，位于一、三象限；k0)的图象经过A(m, 8)，B(4, n)两点，
∴ 8m＝8，4n＝8，
解得m＝1，n＝2，
∴ A(1, 8)，B(4, 2)，
代入一次函数y＝kx+b，可得
8=k+b2=4k+b ，解得k=−2b=10 ，
∴ 一次函数的解析式为y＝−2x+10；
由图可得，kx+b−8x