
2020-2021学年25.3 用频率估计概率教案及反思
展开25.3 用频率估计概率
一、基本目标
【知识与技能】
1.掌握用随机事件的频率估计事件发生的概率的方法.
2.掌握设计试验来估计比较复杂的随机事件发生的概率,并灵活运用概率的有关知识解决实际问题.
【过程与方法】
经历“猜想——试验——收集数据——分析结果”的探索过程,丰富对随机现象的体验,体会概率是描述不确定现象规律的数学模型,理解频率与概率的关系.
【情感态度与价值观】
通过分组合作学习,积累数学活动经验,发展合作交流的意识与能力,逐步建立正确的随机观念,体验数学的价值与学习的乐趣,渗透辩证思想教育.
二、重难点目标
【教学重点】
理解用频率估计概率的条件与方法.
【教学难点】
设计试验来估计比较复杂的随机事件发生的概率.
环节1 自学提纲,生成问题
【5 min阅读】
阅读教材P142~P146的内容,完成下面练习.
【3 min反馈】
1.抛掷一枚质地均匀的硬币时,“正面向上”和“反面向上”发生的可能性__相等__,这两个随机事件发生的概率都是__0.5__.通过试验可以发现,在重复抛掷一枚硬币时,“正面向上”的频率在__0.5__附近摆动.一般地,随着抛掷次数的增加,频率呈现一定的__稳定__性:在__0.5__附近摆动的幅度会越来越__小__.
2.教材P143“思考”的答案是“正面向上”的频率呈现出稳定性,稳定于__0.5__.
3.用频率估计概率时必须做足够的试验才能使频率__稳定于__概率,并且每项试验必须在__相同条件__下进行,试验次数越__多__,得到的频率值就越接近概率,规律就越明显,此时可以用频率的__稳定值__估计事件发生的概率.
环节2 合作探究,解决问题
【活动1】 小组讨论(师生互学)
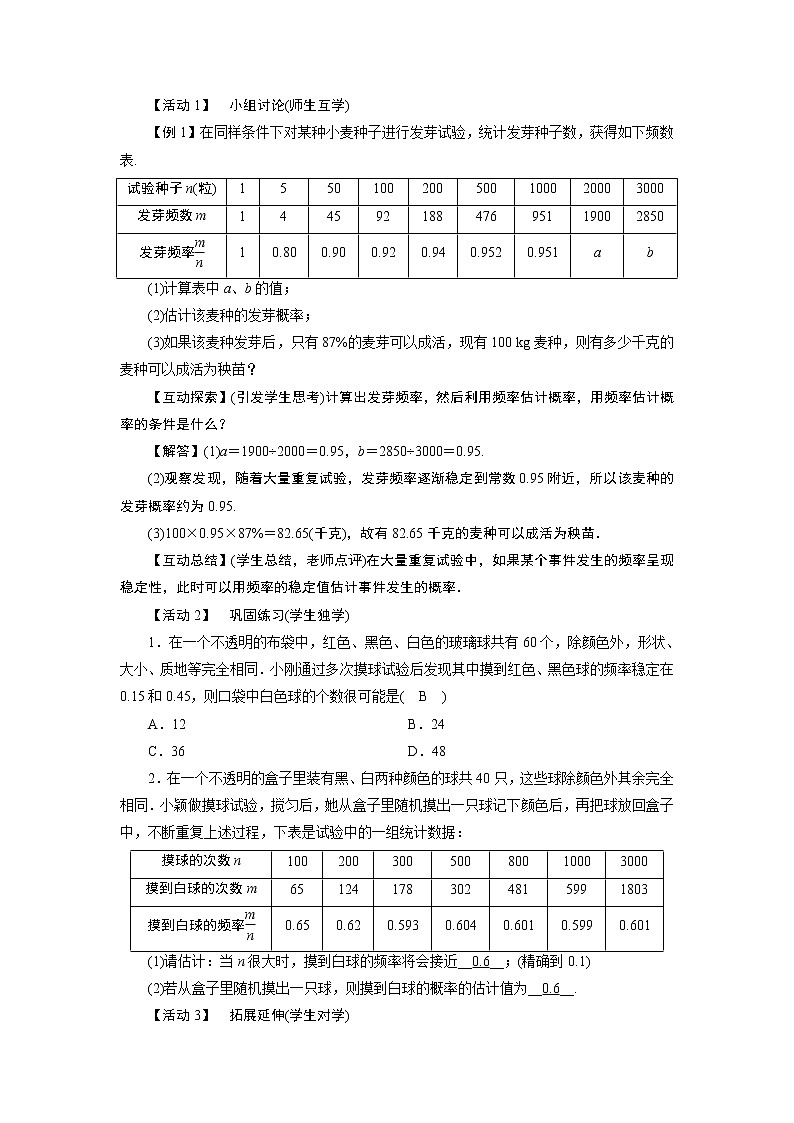
【例1】在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表.
试验种子n(粒) | 1 | 5 | 50 | 100 | 200 | 500 | 1000 | 2000 | 3000 |
发芽频数m | 1 | 4 | 45 | 92 | 188 | 476 | 951 | 1900 | 2850 |
发芽频率 | 1 | 0.80 | 0.90 | 0.92 | 0.94 | 0.952 | 0.951 | a | b |
(1)计算表中a、b的值;
(2)估计该麦种的发芽概率;
(3)如果该麦种发芽后,只有87%的麦芽可以成活,现有100 kg麦种,则有多少千克的麦种可以成活为秧苗?
【互动探索】(引发学生思考)计算出发芽频率,然后利用频率估计概率,用频率估计概率的条件是什么?
【解答】(1)a=1900÷2000=0.95,b=2850÷3000=0.95.
(2)观察发现,随着大量重复试验,发芽频率逐渐稳定到常数0.95附近,所以该麦种的发芽概率约为0.95.
(3)100×0.95×87%=82.65(千克),故有82.65千克的麦种可以成活为秧苗.
【互动总结】(学生总结,老师点评)在大量重复试验中,如果某个事件发生的频率呈现稳定性,此时可以用频率的稳定值估计事件发生的概率.
【活动2】 巩固练习(学生独学)
1.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球试验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是( B )
A.12 B.24
C.36 D.48
2.在一个不透明的盒子里装有黑、白两种颜色的球共40只,这些球除颜色外其余完全相同.小颖做摸球试验,搅匀后,她从盒子里随机摸出一只球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当n很大时,摸到白球的频率将会接近__0.6__;(精确到0.1)
(2)若从盒子里随机摸出一只球,则摸到白球的概率的估计值为__0.6__.
【活动3】 拓展延伸(学生对学)
【例2】均匀的正四面体的各面依次标有1、2、3、4四个数字.小明做了60次投掷试验,结果统计如下:
朝下数字 | 1 | 2 | 3 | 4 |
出现的次数 | 16 | 20 | 14 | 10 |
(1)上述试验中“4朝下”的频率是__________;
(2)“根据试验结果,投掷一次正四面体,出现2朝下的概率是”的说法正确吗?
(3)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
【互动探索】(引发学生思考)结合频率和概率的相关知识,频率和概率有什么区别?(2)问中的说法正确吗?
【解答】(1)
(2)这种说法是错误的.在60次试验中,“2朝下”的频率为并不能说明“2朝下”这一事件发生的概率为.只有当试验的总次数很大时,事件发生的频率才会稳定在相应的事件发生的概率附近.
(3)列表如下:
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
由表可知,总共有16种结果,每种结果出现的可能性相同.
两次朝下数字之和大于4的结果有10种,故P(两次朝下数字之和大于4)==.
【互动总结】(学生总结,老师点评)试验得出的频率只是概率的近似值,试验次数越多,频率越趋向于概率.
环节3 课堂小结,当堂达标
(学生总结,老师点评)
请完成本课时对应练习!
初中数学人教版九年级上册25.3 用频率估计概率精品教案及反思: 这是一份初中数学人教版九年级上册25.3 用频率估计概率精品教案及反思,共8页。教案主要包含了导入新课,探究新知等内容,欢迎下载使用。
人教版九年级上册25.3 用频率估计概率教案及反思: 这是一份人教版九年级上册25.3 用频率估计概率教案及反思,共3页。教案主要包含了教材分析,教学目标,教学重难点,教学方法,教学准备,教学过程,板书设计,教学反思等内容,欢迎下载使用。
初中25.3 用频率估计概率教学设计: 这是一份初中25.3 用频率估计概率教学设计,共8页。教案主要包含了教材分析,学情分析,教学目标,教学重点,教学难点,教学准备,课时安排,教学过程等内容,欢迎下载使用。













