

人教版2021届一轮复习打地基练习 平面与平面平行
展开人教版2021届一轮复习打地基练习 平面与平面平行
一.选择题(共11小题)
1.已知m,n为两条不重合直线,α,β为两个不重合平面,下列条件中,可以作为α∥β的充分条件的是( )
A.m∥n,m⊂α,n⊂β B.m∥n,m⊥α,n⊥β
C.m⊥n,m∥α,n∥β D.m⊥n,m⊥α,n⊥β
2.如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E、F、G、H分别为PA、PD、PC、PB的中点,在此几何体中,给出下面四个结论,其中错误的是( )
A.平面EFGH∥平面ABCD B.BC∥平面PAD
C.AB∥平面PCD D.平面PAD∥平面PAB
3.平面α与平面β平行的条件可以是( )
A.α内有无穷多条直线都与β平行
B.α内的任何直线都与β平行
C.直线a⊂α,直线b⊂β,且a∥β,b∥a
D.直线a∥α,a∥β,且直线a不在α内,也不在β内
4.下列命题中不正确的是( )
A.平面α∥平面β,一条直线a平行于平面α,则a一定平行于平面β
B.平面α∥平面β,则α内的任意一条直线都平行于平面β
C.一个三角形有两条边所在的直线分别平行于一个平面,那么该三角形所在的平面与这个平面平行
D.分别在两个平行平面内的两条直线只能是平行直线或异面直线
5.已知两个不同的平面α,β和两条不同的直线a,b满足a⊂α,b⊂β,则“a∥b”是“α∥β( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.已知直线a、b与平面α、β、γ,下列条件中能推出α∥β的是( )
A.a⊥α且a⊥β B.α⊥γ且β⊥γ
C.a⊂α,b⊂β,a∥b D.a⊂α,b⊂α,a∥β,b∥β
7.两个平面重合的条件是它们的公共部分有( )
A.两个点 B.一条直线与一个点
C.三个点 D.两条平行直线
8.已知角α的两边和角β的两边分别平行,且α=20°,则β=( )
A.20° B.160° C.20°或160° D.不能确定
9.已知平面α,β,直线a⊂α,b⊂β,则“a∥b”是“α∥β”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
10.在长方体ABCD﹣A1B1C1D1中,F,F,G,H分别为棱A1B1,BB1,CC1,C1D1的中点,则下列结论中正确的是( )
A.AD1∥平面EFGH B.BD1∥GH
C.BD∥EF D.平面EFGH∥平面A1BCD1
11.设α,β为两个不同的平面,且直线l是平面α内的一条直线,则l∥β是α∥β的( )
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
二.填空题(共4小题)
12.如图所示,ABCD﹣A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=a3,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= .
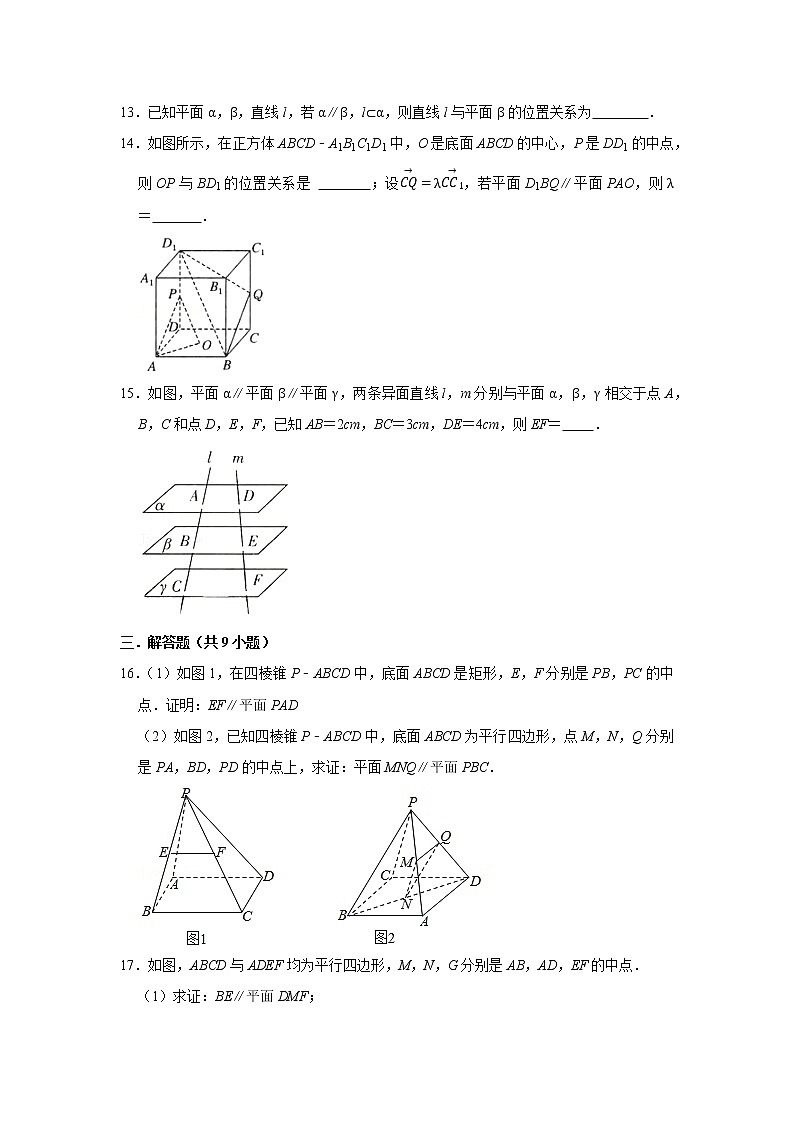
13.已知平面α,β,直线l,若α∥β,l⊂α,则直线l与平面β的位置关系为 .
14.如图所示,在正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,P是DD1的中点,则OP与BD1的位置关系是 ;设CQ→=λCC1→,若平面D1BQ∥平面PAO,则λ= .
15.如图,平面α∥平面β∥平面γ,两条异面直线l,m分别与平面α,β,γ相交于点A,B,C和点D,E,F,已知AB=2cm,BC=3cm,DE=4cm,则EF= .
三.解答题(共9小题)
16.(1)如图1,在四棱锥P﹣ABCD中,底面ABCD是矩形,E,F分别是PB,PC的中点.证明:EF∥平面PAD
(2)如图2,已知四棱锥P﹣ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,求证:平面MNQ∥平面PBC.
17.如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.
(1)求证:BE∥平面DMF;
(2)求证:平面BDE∥平面MNG.
18.如图,在四棱锥P﹣ABCD中,△PAB是等边三角形,BC⊥AB,BC=CD=23,AB=AD=2.
(1)若PC=4,求三棱锥P﹣ABC的体积;
(2)若PB=3BE,则在线段BC上是否存在一点F,使平面AEF∥平面PCD.若存在,求线段BF的长;若不存在,请说明理由.
19.如图所示,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,M,N,Q分别为BC,PA,PB的中点.
(1)求证:平面MNQ∥平面PCD;
(2)在线段PD上是否存在一点E,使得MN∥平面ACE?若存在,求出PEPD的值;若不存在,请说明理由.
20.如图,在正方体ABCDA1B1C1D1中,求证:平面AB1D1∥平面C1BD.
21.如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,F,H,G分别为AC,AD,DE的中点,现将△ACD沿CD折起,如图(乙).求证:平面FHG∥平面ABE.
22.如图,在正方体ABCD﹣A1B1C1D1中,O为底面ABCD的中心,P,Q分别为DD1,CC1的中点.求证:
(1)平面D1BQ∥平面PAO.
(2)求异面直线QD1与AO所成角的余弦值;
23.如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,M、N、P分别是棱DD1、CD、AD的中点.
(1)求证:平面MNP∥平面A1C1B.
(2)将正方体沿平面A1C1B截出一个三棱锥B1﹣A1C1B,求次棱锥的体积与剩下的几何体体积的比.
(3)求直线B1D与直线MN所成的角.
24.已知四棱锥P﹣ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上.
(1)若PM:MA=BN:ND=PQ:QD,求证:平面MNQ∥平面PBC;
(2)若Q满足PQ:QD=2,则M点满足什么条件时,BM∥平面AQC.
人教版2021届一轮复习打地基练习 平面与平面平行
参考答案与试题解析
一.选择题(共11小题)
1.已知m,n为两条不重合直线,α,β为两个不重合平面,下列条件中,可以作为α∥β的充分条件的是( )
A.m∥n,m⊂α,n⊂β B.m∥n,m⊥α,n⊥β
C.m⊥n,m∥α,n∥β D.m⊥n,m⊥α,n⊥β
【分析】根据面面垂直的判定定理,对选项中的命题进行分析、判断正误即可.
【解答】解:由题意知,m∥n,且m⊥α,n⊥β,则α∥β.
故选:B.
2.如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E、F、G、H分别为PA、PD、PC、PB的中点,在此几何体中,给出下面四个结论,其中错误的是( )
A.平面EFGH∥平面ABCD B.BC∥平面PAD
C.AB∥平面PCD D.平面PAD∥平面PAB
【分析】把图形还原为一个四棱锥,然后根据线面、面面平行的判定定理逐一判断即可.
【解答】解:把图形还原为一个四棱锥,如图所示,
对于A,因为E,F分别是PA,PD的中点,所以EF∥AD,
又EF⊄平面ABCD,AD⊂平面ABCD,
所以EF∥平面ABCD,同理EH∥平面ABDCD,
又EH∩EF=E,EF,EH⊂平面EFGH,所以平面EFGH∥平面ABCD,故选项A正确;
对于B,因为BC∥AD,BC⊄平面PAD,AD⊂平面PAD,所以BC∥平面PAD,故B正确;
对于C,AB∥CD,AB⊄平面PCD,CD⊂平面PCD,所以AB∥平面PCD,故C正确;
对于D,平面PAD∩平面PAB=PA,故D错误.
故选:D.
3.平面α与平面β平行的条件可以是( )
A.α内有无穷多条直线都与β平行
B.α内的任何直线都与β平行
C.直线a⊂α,直线b⊂β,且a∥β,b∥a
D.直线a∥α,a∥β,且直线a不在α内,也不在β内
【分析】利用平面与平面平行的判定定理,逐个分析A,B,C,D四个选项,能够得到正确结果.
【解答】解:α内有无穷多条直线与β平行,并不能保证α内有两条相交直线与β平行,
这无穷多条直线可以是一组平行线,故A错误;
α内的任何直线都与β平行,则α内至少有两条相交直线与β平行,
所以平面α与平面β平行,故B正确;
直线a⊂α,直线b⊂β,且a∥β,b∥a,
当直线a∥b时,同样不能保证平面α与平面β平行,故C不正确;
直线a∥α,a∥β,且直线a不在α内,也不在β内,
直线a可以是平行平面α与平面β的相交直线,
故不能保证平面α与平面β平行,故D不正确.
故选:B.
4.下列命题中不正确的是( )
A.平面α∥平面β,一条直线a平行于平面α,则a一定平行于平面β
B.平面α∥平面β,则α内的任意一条直线都平行于平面β
C.一个三角形有两条边所在的直线分别平行于一个平面,那么该三角形所在的平面与这个平面平行
D.分别在两个平行平面内的两条直线只能是平行直线或异面直线
【分析】由空间直线与平面,平面与平面的平行关系判断每一选项可得答案,
【解答】解:A、平面α∥平面β,一条直线a平行于平面α,则a一定平行于平面β;因为a有可能在β内;故错误;
B、平面α∥平面β,则α内的任意一条直线都平行于平面β,由面面平行可得一个平面内的线与另一平面平行,故正确;
C、一个三角形有两条边所在的直线分别平行于一个平面,那么该三角形所在的平面与这个平面平行,由面面平行的判定可知语句正确;
D、分别在两个平行平面内的两条直线只能是平行直线或异面直线;由面面平行的性质可知语句正确;
故选:A.
5.已知两个不同的平面α,β和两条不同的直线a,b满足a⊂α,b⊂β,则“a∥b”是“α∥β( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【分析】结合长方体分析线面关系,举反例即可.
【解答】(1)证明充分性,如图所示:
设α为长方体上底面,a⫋α;设β为长方体前面,b⫋β;
满足a∥b,但α⊥β,即“a∥b”不是“α∥β的充分条件;
(1)证明必要β性,如图所示:
设α为长方体上底面,a⫋α;设β为长方体下底面,b⫋β;
满足α∥β,但直线a与b异面,即“a∥b”不是“α∥β的必要条件;
故选:D.
6.已知直线a、b与平面α、β、γ,下列条件中能推出α∥β的是( )
A.a⊥α且a⊥β B.α⊥γ且β⊥γ
C.a⊂α,b⊂β,a∥b D.a⊂α,b⊂α,a∥β,b∥β
【分析】根据垂直于同一直线的两个平面平行可知选项A是否正确;平面与平面垂直的性质,判断选项B的正误,对于选项C可知两个平面可能相交,选项D,若a与b平行时,两平面相交,对选项逐一判断即可.
【解答】解:选项A,根据垂直于同一直线的两个平面平行,可知正确;
选项B,α⊥γ,β⊥γ可能推出α、β 相交,所以B不正确;
选项C,a⊂α,b⊂β,a∥b,α与β 可能相交,故不正确;
选项D,a⊂α,b⊂α,a∥β,b∥β,如果a∥b推出α、β 相交,所以D不正确;
故选:A.
7.两个平面重合的条件是它们的公共部分有( )
A.两个点 B.一条直线与一个点
C.三个点 D.两条平行直线
【分析】本题考查能唯一确定平面的条件,根据公理2,过不共线的三点可确定唯一平面,即可选出答案.
【解答】解:因为过不共线的三点可确定唯一平面,
A选项只有两个点,
B选项应该改为直线和直线外一点,
C选项应该改为不共线的三个点,
D选项两条平行直线可确定唯一平面,
故选:D.
8.已知角α的两边和角β的两边分别平行,且α=20°,则β=( )
A.20° B.160° C.20°或160° D.不能确定
【分析】根据两角的两边互相平行得出两角相等或互补,得出方程,求出即可:
【解答】解:∵∠α与∠β的两边分别平行,∴∠α+∠β=180°或∠α=∠β.
∵α=20°,∴∠β=180°﹣20°=160°,或∠β=20°.
故选:C.
9.已知平面α,β,直线a⊂α,b⊂β,则“a∥b”是“α∥β”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【分析】充分条件和必要条件的定义结合空间线线、面面的位置关系进行判断即可.
【解答】解:已知平面α,β,直线a⊂α,b⊂β
∵a∥b推不出α∥β,
α∥β推不出a∥b,
∴a∥b是α∥β的既不充分也不必要条件.
故选:D.
10.在长方体ABCD﹣A1B1C1D1中,F,F,G,H分别为棱A1B1,BB1,CC1,C1D1的中点,则下列结论中正确的是( )
A.AD1∥平面EFGH B.BD1∥GH
C.BD∥EF D.平面EFGH∥平面A1BCD1
【分析】在A中,AD1与平面AD1BC1相交,且平面EFGH∥平面AD1BC1,从而AD1与平面EFGH相交;在B中,BD1∩CD1=D1,CD1∥GH,从而BD1不可能平行于GH;在C中,BD∩A1B=B,A1B∥EF,从而BD与EF不可能平行;在D中,EF∥A1B,FG∥BC,从而平面EFGH∥平面A1BCD1.
【解答】解:在长方体ABCD﹣A1B1C1D1中,
F,F,G,H分别为棱A1B1,BB1,CC1,C1D1的中点
在A中,∵AD1与平面AD1BC1相交,且平面EFGH∥平面AD1BC1,
∴AD1与平面EFGH相交,故A错误;
在B中,BD1∩CD1=D1,CD1∥GH,故BD1不可能平行于GH,故B错误;
在C中,BD∩A1B=B,A1B∥EF,故BD与EF不可能平行,故C错误;
在D中,EF∥A1B,FG∥BC,A1B∩BC=B,EF∩FG=F,
∴平面EFGH∥平面A1BCD1,故D正确.
故选:D.
11.设α,β为两个不同的平面,且直线l是平面α内的一条直线,则l∥β是α∥β的( )
A.充分必要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
【分析】利用面面平行和线面平行的定义和性质,结合充分条件和必要条件的定义进行判断.
【解答】解:根据面面平行的性质,由α∥β,l为平面内α的一条直线,得到l∥β,
当l∥β,则α∥β或相交,
故l∥β是α∥β的必要不充分条件,
故选:C.
二.填空题(共4小题)
12.如图所示,ABCD﹣A1B1C1D1是棱长为a的正方体,M、N分别是下底面的棱A1B1,B1C1的中点,P是上底面的棱AD上的一点,AP=a3,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= 223a .
【分析】由题设PQ在直角三角形PDQ中,故需要求出PD,QD的长度,用勾股定理在直角三角形PDQ中求PQ的长度.
【解答】解:∵平面ABCD∥平面A1B1C1D1,MN⊂平面A1B1C1D1
∴MN∥平面ABCD,又PQ=面PMN∩平面ABCD,
∴MN∥PQ.
∵M、N分别是A1B1、B1C1的中点
∴MN∥A1C1∥AC,
∴PQ∥AC,又AP=a3,ABCD﹣A1B1C1D1是棱长为a的正方体,
∴CQ=a3,从而DP=DQ=2a3,
∴PQ=DQ2+DP2=(2a3)2+(2a3)2=223a.
故答案为:223a
13.已知平面α,β,直线l,若α∥β,l⊂α,则直线l与平面β的位置关系为 l∥β .
【分析】根据平面与平面平行的定义可以得出直线与平面平行.
【解答】解:因为平面α∥β,且l⊂α,
所以l∥β.
故答案为:l∥β.
14.如图所示,在正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,P是DD1的中点,则OP与BD1的位置关系是 平行 ;设CQ→=λCC1→,若平面D1BQ∥平面PAO,则λ= 12 .
【分析】利用空间向量的平行判断两直线平行即可;
根据两平面平行,向量平行可得结果.
【解答】解:如图所示,
分别以DA,DC,DD,所在直线为x轴、y轴、z轴,建立空间直角坐标系Dxyx,
设正方体的棱长为1,
则O(12,12,0),C(0,1,0),C1(0,1,1),P(0,0,12),#/DEL/#A(1,0,0),B(1,1,0),D1(0,0,1)#/DEL/#
则OP→=(−12,−12,12),BD1→=(−1,−1,1),
∴OP→=12BD1→,
∴OP//BD1
设Q(0,1,z),
则BQ→=(−1,0,z),
由于OP//BD1,故要使平面D1BQ//平面 PAO,
则Q(0,1,12),
由CQ→=(0,0,12),CC1→=(0,0,1)及CQ→=λCC1→得:λ=12.
15.如图,平面α∥平面β∥平面γ,两条异面直线l,m分别与平面α,β,γ相交于点A,B,C和点D,E,F,已知AB=2cm,BC=3cm,DE=4cm,则EF= 6 .
【分析】连接AF,交β于G,从而利用两平行平面的性质定理得线线平行,再由平行直线分线段成比例定理即可得解.
【解答】解:连接AF,交平面β于点G,连接EG,BG,AD,CF,如右图所示.
∵l∩AF=A,∴l与AF确定一个平面,设为α1,
∵γ∩α1=CF,β∩α1=BG,且γ∥β,
∴CF∥BG,
∴ABBC=AGGF.
同理可证GE∥AD,
∴AGGF=DEEF,
∴ABBC=DEEF.
∴EF=BC⋅DEAB=3×42=6.
故答案为:6.
三.解答题(共9小题)
16.(1)如图1,在四棱锥P﹣ABCD中,底面ABCD是矩形,E,F分别是PB,PC的中点.证明:EF∥平面PAD
(2)如图2,已知四棱锥P﹣ABCD中,底面ABCD为平行四边形,点M,N,Q分别是PA,BD,PD的中点上,求证:平面MNQ∥平面PBC.
【分析】(I)由E、F分别是PB、PC的中点,可由三角形中位线定理得到EF∥BC,进而根据底面是矩形,对边平行得到EF∥AD,结合线面平行的判定定理得到EF∥平面PAD;
(2)由MN∥PB,MQ∥BC可得平面MNQ∥平面PBC
【解答】证明:(Ⅰ)∵E、F分别是PB、PC的中点,
∴EF∥BC.
∵底面ABCD是矩形,
∴AD∥BC.
∴EF∥AD.
又AD⊂平面PAD,EF⊄平面PAD,
∴EF∥平面PAD.
(2)∵点M,N,Q分别是PA,BD,PD的中点,
∴MQ∥AD,QN∥PB,
∵底面ABCD为平行四边形,
∴AD∥BC.
∴MQ∥BC,
∵MQ∩MN=N,PB∩BC=B,
∴平面MNQ∥平面PBC.
17.如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.
(1)求证:BE∥平面DMF;
(2)求证:平面BDE∥平面MNG.
【分析】(1)由面面平行推出线面平行即可;(2)由线线平行推出面面平行即可.
【解答】解:如图示:
,
作DC的中点P,连接PE、PB,
ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.
∴PB∥DM,FM∥PE,且FM,MD交于M点,PB,PE交于P点,
故平面DFM∥平面BPE,
∴BE∥平面DMF;
(2)∵MN∥BD,GN∥DE,且MN、GN交于N点,DE、DB交于D点,
∴平面BDE∥平面MNG.
18.如图,在四棱锥P﹣ABCD中,△PAB是等边三角形,BC⊥AB,BC=CD=23,AB=AD=2.
(1)若PC=4,求三棱锥P﹣ABC的体积;
(2)若PB=3BE,则在线段BC上是否存在一点F,使平面AEF∥平面PCD.若存在,求线段BF的长;若不存在,请说明理由.
【分析】(1)推导出BC⊥PB,BC⊥AB,从而BC⊥平面PAB.由此能求出三棱锥P﹣ABC的体积.
(2)作EF∥PC,交BC于F,连接AF.则E是PB的三等分点,可得BF=233.推导出△ABC≌△ADC,推导出AF∥平面PCD.EF∥平面PCD.从而平面AEF∥平面PCD.由此得到在线段BC上存在一点F,使平面AEF∥平面PCD.此时BF=233.
【解答】解:(1)因为△PAB是等边三角形,AB=2,
所以PB=2.又因为PC=4,BC=23,
所以PC2=PB2+BC2,所以BC⊥PB.
又BC⊥AB,AB,PB⊂平面PAB,AB∩PB=B,
所以BC⊥平面PAB.
S△PAB=12×2×2×sin60°=3,
所以三棱锥P﹣ABC的体积V=13S△PAB⋅BC=13×3⋅23=2.
(2)在线段BC上存在一点F,使平面AEF∥平面PCD.此时BF=233.
理由如下:
如图,作EF∥PC,交BC于F,连接AF.
因为PB=3BE,所以E是PB的三等分点,可得BF=233.
因为AB=AD=2,BC=CD=23,AC=AC,
所以△ABC≌△ADC,因为BC⊥AB,所以∠ABC=90°,
因为tan∠ACB=ABBC=223=33,
所以∠ACB=∠ACD=30°,所以∠BCD=60°,
因为tan∠AFB=ABBF=2233=3,所以∠AFB=60°,所以AF∥CD,
因为AF⊄平面PCD,CD⊂平面PCD,所以AF∥平面PCD.
又EF∥PC,EF⊄平面PCD,PC⊂平面PCD,所以EF∥平面PCD.
因为AF∩EF=F,AF、EF⊂平面AEF,所以平面AEF∥平面PCD.
所以在线段BC上存在一点F,使平面AEF∥平面PCD.此时BF=233.
19.如图所示,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,M,N,Q分别为BC,PA,PB的中点.
(1)求证:平面MNQ∥平面PCD;
(2)在线段PD上是否存在一点E,使得MN∥平面ACE?若存在,求出PEPD的值;若不存在,请说明理由.
【分析】(1)推导出NQ∥CD,MQ∥PC,由此能证明平面MNQ∥平面PCD.
(2)取PD中点E,连接NE、CE,推导出四边形MCEN是平行四边形,从而MN∥CE,由此能求出MN∥平面ACE,且PEPD=12.
【解答】证明:(1)∵在四棱锥P﹣ABCD中,底面ABCD是平行四边形,M,N,Q分别为BC,PA,PB的中点,
∴NQ∥CD,MQ∥PC,
∵NQ∩MQ=Q,CD∩PC=C,且NQ、MQ⊂平面MNQ,CD、PC⊂平面PCD,
∴平面MNQ∥平面PCD.
解:(2)线段PD上存在一点E,使得MN∥平面ACE,且PEPD=12.
证明如下:
取PD中点E,连接NE、CE,
∵N、E、M分别是AP、PD、BC的中点,BC∥=AD,
∴NE∥=NE,∴四边形MCEN是平行四边形,∴MN∥CE,
∵MN⊄平面ACE,CE⊂平面ACE,
∴MN∥平面ACE,且PEPD=12.
20.如图,在正方体ABCDA1B1C1D1中,求证:平面AB1D1∥平面C1BD.
【分析】利用直方图与平行四边形的性质可得:BC1∥AD1,利用线面平行的判定定理可得BC1∥平面AB1D1,同理可得:BD∥平面AB1D1,即可证明:平面C1BD∥平面AB1D1.
【解答】证明:∵ABCD﹣A1B1C1D1为正方体,
∴在平行四边形ABC1D1中,BC1∥AD1,
又AD1⊂平面AB1D1,BC1⊄平面AB1D1,
∴BC1∥平面AB1D1,
同理可得:BD∥平面AB1D1,且BC1∩BD=B,
∴平面C1BD∥平面AB1D1.
21.如图(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,F,H,G分别为AC,AD,DE的中点,现将△ACD沿CD折起,如图(乙).求证:平面FHG∥平面ABE.
【分析】推导出FH∥CD,HG∥AE,CD∥BE,FH∥BE,从而FH∥平面ABE,HG∥平面ABE,由此能证明平面FHG∥平面ABE.
【解答】证明:∵F,H,G分别为AC,AD,DE的中点,
∴FH∥CD,HG∥AE,
∵AB⊥CD,AB⊥BE,
∴CD∥BE,∴FH∥BE,
∵BE⊂平面ABE,FH⊄平面ABE,
∴FH∥平面ABE,
∵AE⊂平面ABE,HG⊄平面ABE,∴HG∥平面ABE,
∵FH∩HG=H,
∴平面FHG∥平面ABE.
22.如图,在正方体ABCD﹣A1B1C1D1中,O为底面ABCD的中心,P,Q分别为DD1,CC1的中点.求证:
(1)平面D1BQ∥平面PAO.
(2)求异面直线QD1与AO所成角的余弦值;
【分析】(1)连接PQ、BD,四边形PABQ为平行四边形,从而AP∥BQ,进而BQ∥面AOP,同理可证D1B∥面AOP,由此能证明面BQD1∥面AOP.
(2)连接OC,CP,由CP∥QD1,可求异面直线QD1与AO所成角为∠ACP,设正方体ABCD﹣A1B1C1D1,的边长为1,可求AP,AC,PC的值,由余弦定理可得cos∠ACP的值,即可得解.
【解答】解:(1)证明:连接PQ、BD,由已知得四边形PABQ为平行四边形,
∴AP∥BQ,
∵AP⊂面AOP,BQ⊄面AOP,
∴BQ∥面AOP,…(2分)
同理可证D1B∥面AOP,
又∵BQ∩D1B=B,BQ⊂面BQD1,BD1⊂面BQD1,
∴面BQD1∥面AOP.…(6分)
说明:直接用线线平行到面面平行时扣(2分)
(2)连接OC,CP,
∵CP∥QD1,
∴异面直线QD1与AO所成角为∠ACP,
∵设正方体ABCD﹣A1B1C1D1,的边长为1,
在△ACP中,可得:AP=12+(12)2=52,AC=12+12=2,PC=12+(12)2=52,
∴由余弦定理可得:cos∠ACP=CP2+AC2−AP22AC⋅CP=54+2−542×2×52=105,
即异面直线QD1与AO所成角余弦值为105.
23.如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,M、N、P分别是棱DD1、CD、AD的中点.
(1)求证:平面MNP∥平面A1C1B.
(2)将正方体沿平面A1C1B截出一个三棱锥B1﹣A1C1B,求次棱锥的体积与剩下的几何体体积的比.
(3)求直线B1D与直线MN所成的角.
【分析】(1)通过证明AC∥A1C1,证明AC∥平面A1C1B,根据AC∥PN,可证PN∥平面A1C1B,同理MN∥平面A1C1B,由面面平行的判定定理得平面MNP∥平面A1C1B;
(2)计算截去的三棱锥的体积,可得截去的三棱锥的体积与剩下的几何体体积的比;
(3)先证DC1为DB1在平面CDD1C1内的射影,再根据三垂线定理证明MN⊥DB1,可得直线B1D与直线MN所成的角.
【解答】解:(1)证明:连接AC,∵AA1∥CC1,又AA1=CC1,
∴四边形ACC1A1为平行四边形,AC∥A1C1,AC⊄平面A1C1B,∴AC∥平面A1C1B,
又AC∥PN,∴PN∥平面A1C1B,
同理MN∥平面A1C1B,又MN∩PN=N,∴平面MNP∥平面A1C1B;
(2)VB1−A1C1B=13×12×a×a×a=16a3,
∴截去的三棱锥的体积与剩下的几何体体积的比为1:5;
(3)连接DC1,CD1,∵B1C1⊥平面CDD1C1,∴DC1为DB1在平面CDD1C1内的射影,
∵DC1⊥CD1,又MN∥CD1,由三垂线定理得:MN⊥DB1,
即直线B1D与直线MN所成的角为90°.
24.已知四棱锥P﹣ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上.
(1)若PM:MA=BN:ND=PQ:QD,求证:平面MNQ∥平面PBC;
(2)若Q满足PQ:QD=2,则M点满足什么条件时,BM∥平面AQC.
【分析】(1)由已知比例式分别证明QM∥BC,QN∥PB,进一步得到MQ∥平面PBC,即QN∥平面PBC,再由面面平行的判定可得平面MNQ∥平面PBC;
(2)连接AC,交BD于O,连接OQ,取PQ的中点G,连接BG,则BG∥OQ,可得BG∥平面AQC,取PA的中点M,连接GM,则GM∥AQ,可得GM∥平面AQC,从而得到平面BGM∥平面AQC,则BM∥平面AQC,此时M为PA的中点.
【解答】(1)证明:∵PM:MA=PQ:QD.
∴QM∥AD,∵AD∥BC,∴QM∥BC,
∵QM⊄平面PBC,BC⊂平面PBC,
∴MQ∥平面PBC.
∵BN:ND=PQ:QD.∴QN∥PB,
即QN∥平面PBC.
∵QM∩QN=Q,∴平面MNQ∥平面PBC;
(2)解:连接AC,交BD于O,连接OQ,
取PQ的中点G,连接BG,则BG∥OQ,
∵OQ⊂平面AQC,BG⊄平面AQC,∴BG∥平面AQC,
取PA的中点M,连接GM,则GM∥AQ,
∵AQ⊂平面AQC,GM⊄平面AQC,∴GM∥平面AQC,
又BG∩GM=G,∴平面BGM∥平面AQC,
则BM∥平面AQC,此时M为PA的中点.
人教版2022届一轮复习打地基练习 平面向量几本定理: 这是一份人教版2022届一轮复习打地基练习 平面向量几本定理,共32页。
人教版2022届一轮复习打地基练习 平面向量坐标运算: 这是一份人教版2022届一轮复习打地基练习 平面向量坐标运算,共13页。试卷主要包含了已知向量a→=,若向量a→=,在平行四边形ABCD中,已知A,向量a→=等内容,欢迎下载使用。
人教版2022届一轮复习打地基练习 平面向量共线的坐标表示: 这是一份人教版2022届一轮复习打地基练习 平面向量共线的坐标表示,共19页。试卷主要包含了已知向量a→=,设向量a→=,已知向量a→=,b→=,已知点A,已知向量m→=,若⊥,则t=,若向量a→=等内容,欢迎下载使用。












