人教版2022届一轮复习打地基练习 等可能事件和等可能事件的概率

这是一份人教版2022届一轮复习打地基练习 等可能事件和等可能事件的概率，共26页。试卷主要包含了若在区间，如图是一块高尔顿板示意图等内容，欢迎下载使用。
人教版2022届一轮复习打地基练习 等可能事件和等可能事件的概率
一．选择题（共16小题）
1．2021年起，我省将实行“3+1+2”高考模式，某中学为了解本校学生的选考情况，随机调查了100位学生，其中选考化学或生物的学生共有70位，选考化学的学生共有40位，选考化学且选考生物的学生共有20位．若该校共有1500位学生，则该校选考生物的学生人数的估计值为（　　）
A．300 B．450 C．600 D．750
2．某中学举行校园歌手大赛，经预赛后共10名同学进入决赛，现采用抽签方式确定出场顺序，若甲同学先抽，则他抽到的出场序号小于4的概率为（　　）
A．710 B．15 C．25 D．310
3．若在区间（﹣1，1）内任取实数a，在区间（0，1）内任取实数b，则直线ax﹣by＝0与圆（x﹣1）2+（y﹣2）2＝1相交的概率为（　　）
A．38 B．516 C．58 D．316
4．已知关于x的方程﹣2x2+bx+c＝0，若b，c∈{0，1，2，3}，记“该方程有实数根x1，x2且满足﹣1≤x1≤x2≤2”为事件A，则事件A发生的概率为（　　）
A．14 B．34 C．78 D．1516
5．甲袋中装有白球3个，黑球5个，乙袋内装有白球4个，黑球6个．现从甲袋内随机抽取一个球放入乙袋，充分掺混后再从乙袋内随机抽取一球放入甲袋，则甲袋中的白球没有减少的概率为（　　）
A．3714 B．3544 C．2544 D．544
6．从数字1，2，3，4，5这五个数中，随机抽取2个不同的数，则这2个数的和为偶数的概率是（　　）
A．15 B．25 C．35 D．45
7．某校3名教师和5名学生共8人去北京参加学习方法研讨会，需乘坐两辆车，每车坐4人，则恰有两名教师在同一车上的概率（　　）
A．13 B．37 C．67 D．56
8．如图是一个正方体纸盒的展开图，把1，1，2，2，3，3分别填入小正方形后，按虚线折成正方体，则所得到的正方中体相对面上的两个数都相等的概率是（　　）

A．415 B．16 C．115 D．120
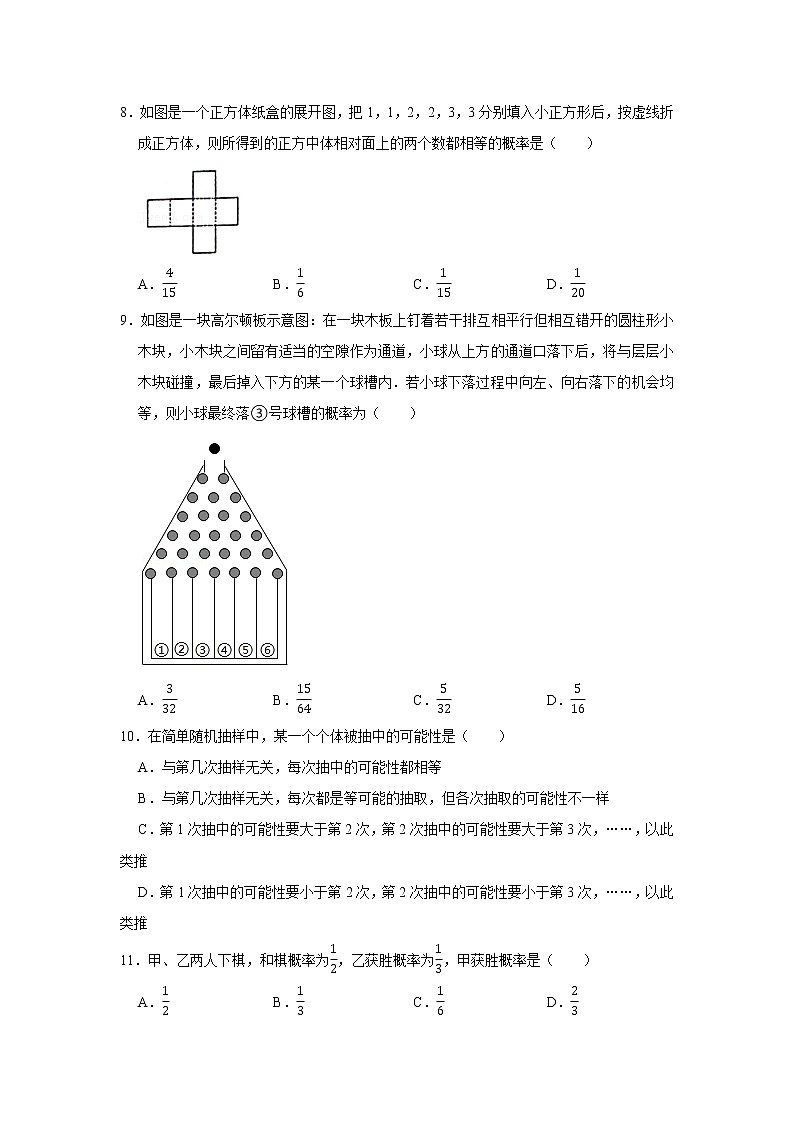
9．如图是一块高尔顿板示意图：在一块木板上钉着若干排互相平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，小球从上方的通道口落下后，将与层层小木块碰撞，最后掉入下方的某一个球槽内．若小球下落过程中向左、向右落下的机会均等，则小球最终落③号球槽的概率为（　　）

A．332 B．1564 C．532 D．516
10．在简单随机抽样中，某一个个体被抽中的可能性是（　　）
A．与第几次抽样无关，每次抽中的可能性都相等
B．与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能性不一样
C．第1次抽中的可能性要大于第2次，第2次抽中的可能性要大于第3次，……，以此类推
D．第1次抽中的可能性要小于第2次，第2次抽中的可能性要小于第3次，……，以此类推
11．甲、乙两人下棋，和棋概率为12，乙获胜概率为13，甲获胜概率是（　　）
A．12 B．13 C．16 D．23
12．从(3x+1x)10的展开式中任选一项，使选出的项中x的幂指数为整数的概率为（　　）
A．111 B．211 C．311 D．411
13．某项试验的成功率是失败率的2倍，用随机变量ξ描述一次试验成功的次数，则P（ξ＝0）等于（　　）
A．0 B．12 C．13 D．23
14．古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米2016石，验得米内夹谷，抽样取米一把，数得270粒内夹谷30粒，则这批米内夹谷约为（　　）
A．222石 B．224石 C．230石 D．232石
15．中共一大会址（现上海市兴业路76号）、江西井冈山（中共革命根据地）、贵州遵义（遵义会议召开地）、陕西延安（中共革命圣地）是中学生的几个重要的研学旅行地（只是部分）．某中学在校学生3000人，学校团委为了了解本校学生到上述红色基地研学旅行的情况，随机调查了500名学生，其中到过中共一大会址或井冈山研学旅行的共有40人，到过井冈山研学旅行的20人，到过中共一大会址并且到过井冈山研学旅行的恰有10人，根据这项调查，估计该学校到过中共一大会址研学旅行的学生大约有（　　）人．
A．240 B．180 C．120 D．60
16．从1，2，3，4这4个数中，不放回地任意取两个数，两个数都是奇数的概率是（　　）
A．16 B．14 C．13 D．12
二．填空题（共14小题）
17．从4名男生和3名女生中选出4人去参加辩论比赛，则选出的4人中至少有2名男生的概率为　 　．（用数字作答）
18．如果生男孩和生女孩的概率相等，则有3个小孩的家庭中至少有2个女孩的概率是　 　．
19．一个不透明的袋中装有5个白球、4个红球（9个球除颜色外其余完全相同），经充分混合后，从袋中随机摸出3球，则摸出的3球中至少有一个是白球的概率为　 　．
20．同时掷两粒骰子，则点数之和为7的概率是　 　．（结果用分数表示）
21．有编号分别为1，2，3，4，5的5个红球和5个黑球，从中随机取出4个，则取出球的编号互不相同的概率为　 　．
22．我校2019级高一新生1800人．根据入校体验的视力数据库，我们抽取了50个样本，其中“视力不低于5.0”有27个．由此可以估计我校2019级高一新生中“视力不低于5.0”的比例约为　 　．
23．古代“五行”学说认为：“物质分金、木、水、火、土五种属性，金克木、木克土，土克水，水克火，火克金”，从这五种不同属性的物质中随机抽取两种，则抽取的两种物质不相克的概率是　 　．
24．某小组共有10名学生，其中女生3名，现选举2名代表，至少有1名女生当选的概率为　 　．
25．玲玲和倩倩是一对好朋友，她俩都想去观看某歌星的演唱会，可手里只有一张票，怎么办呢？玲玲对倩倩说：“我向空中抛两枚同样的一元硬币，如果落地后一正一反，我就去，如果落地后两面一样，你就去！”这个办法　 　.（选填“公平”或“不公平”）
26．我国古代数学名著《九章算术》中有“米谷粒分”题：粮仓开仓收粮，有人送来米1536石，验得米内夹谷，抽样取米一把，数得256粒内夹谷18粒，则这批米内夹谷约为　 　
27．口袋内装有一些大小相同的红球、黄球和蓝球，从中摸出1个球，摸出红球的概率为0.42，摸出黄球的概率是0.28．若红球有21个，则蓝球有　 　个．
28．在抛掷一颗骰子（一种正方体玩具，六个面标有1，2，3，4，5，6字样）的试验中，事件A表示“不大于4的偶数点出现”，事件B表示“小于5的点数出现”，则事件A+B的概率为　 　．
29．为估计池塘中鱼的数量，负责人将50条带有标记的同品种鱼放入池塘，几天后，随机打捞40条鱼，其中带有标记的共5条．利用统计与概率知识可以估计池塘中原来有鱼　 　条．
30．口袋里有3个红球，2个白球，质地均匀，形状完全相同，从中任意摸出两个球，两个都是红球的概率　 　．
三．解答题（共8小题）
31．在10件产品中有一等品6件，二等品2件（一等品和二等品都是正品），其余为次品．
（Ⅰ）从中任取2件进行检测，2件都是一等品的概率是多少？
（Ⅱ）从中任取2件进行检测，2件中至少有一件次品的概率是多少？
（Ⅲ）如果对产品逐个进行检测，且已检测到前3次均为正品，则第4次检测的产品仍为正品的概率是多少？
32．某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．
（Ⅰ）估计这次测试数学成绩的平均分；
（Ⅱ）假设在[90，100]段的学生的数学成绩都不相同，且都在94分以上，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数中任取2个数，求这两个数恰好是在[90，100]段的两个学生的数学成绩的概率．

33．将一枚质地均匀且四个面上分别标有1，2，3，4的正四面体先后抛掷两次，其底面落于桌面上，记第一次朝下面的数字为x，第二次朝下面的数字为y
（1）求满足条件“xy为整数”的事件的概率；
（2）求满足条件“x﹣y＜2”的事件的概率．
34．某电子原件生产厂生产的10件产品中，有8件一级品，2件二级品，一级品和二级品在外观上没有区别．从这10件产品中任意抽检2件，计算：
（1）2件都是一级品的概率；
（2）至少有一件二级品的概率．
35．学生会6名同学，其中4名男同学2名女同学．现要从中随机选出2名代表发言．求：
（1）A同学被选中的概率是多少？
（2）至少有1名女同学被选中的概率是多少？
36．一个口袋内装有大小相同的5个球，3个白球，2个黑球，从中一次摸出两个球．
求：（1）共有多少个基本事件；
（2）摸出2个白球的概率．
37．在一个池塘中有1000条鱼，其中有100条草鱼．现从中捕出20条鱼．试计算其中至少有两条草鱼的概率．
38．袋子中装有编号为A1，A2，A3的3个黑球和编号为B1，B2的2个红球，从中任意摸出2个球．
（1）写出所有不同的结果；
（2）求恰好摸出1个黑球和1个红球的概率；
（3）求至少摸出1个红球的概率．

人教版2022届一轮复习打地基练习 等可能事件和等可能事件的概率
参考答案与试题解析
一．选择题（共16小题）
1．2021年起，我省将实行“3+1+2”高考模式，某中学为了解本校学生的选考情况，随机调查了100位学生，其中选考化学或生物的学生共有70位，选考化学的学生共有40位，选考化学且选考生物的学生共有20位．若该校共有1500位学生，则该校选考生物的学生人数的估计值为（　　）
A．300 B．450 C．600 D．750
【分析】推导出100名学生中考生物的学生有：70﹣40+20＝50．该校共有1500位学生，由此能求出该校选考生物的学生人数的估计值．
【解答】解：某中学为了解本校学生的选考情况，随机调查了100位学生，
其中选考化学或生物的学生共有70位，选考化学的学生共有40位，
选考化学且选考生物的学生共有20位．
∴100名学生中考生物的学生有：70﹣40+20＝50．
该校共有1500位学生，则该校选考生物的学生人数的估计值为1500×50100=750．
故选：D．
2．某中学举行校园歌手大赛，经预赛后共10名同学进入决赛，现采用抽签方式确定出场顺序，若甲同学先抽，则他抽到的出场序号小于4的概率为（　　）
A．710 B．15 C．25 D．310
【分析】甲同学先抽，基本事件总数n＝10，他抽到的出场序号小于4包含的基本事件个数m＝3，由此能求出他抽到的出场序号小于4的概率．
【解答】解：某中学举行校园歌手大赛，经预赛后共10名同学进入决赛，
现采用抽签方式确定出场顺序，
甲同学先抽，基本事件总数n＝10，
他抽到的出场序号小于4包含的基本事件个数m＝3，
则他抽到的出场序号小于4的概率为p=310．
故选：D．
3．若在区间（﹣1，1）内任取实数a，在区间（0，1）内任取实数b，则直线ax﹣by＝0与圆（x﹣1）2+（y﹣2）2＝1相交的概率为（　　）
A．38 B．516 C．58 D．316
【分析】由题意可得本题是几何概率模型，先求构成试验的全部区域：−1＜a＜10＜b＜1所围成的图形的面积，记：“直线ax﹣by＝0与圆（x﹣1）2+（y﹣2）2＝1相交”为事件A，则由直线与圆相交的性质可得，|a−2b|a2+b2＜1整理可得4a﹣3b＞0，再求构成区域A的面积，代入几何概型计算公式可求
【解答】解：由题意可得构成试验的全部区域为：−1＜a＜10＜b＜1所围成的边长分别为1，2的矩形，面积为2
记：“直线ax﹣by＝0与圆（x﹣1）2+（y﹣2）2＝1相交”为事件A
则由直线与圆相交的性质可得，|a−2b|a2+b2＜1整理可得4a﹣3b＞0，构成区域A为图中阴影部分，面积为(14+1)×1×12=58
由几何概率的计算公式可得，P（A）=582=516
故选B．

4．已知关于x的方程﹣2x2+bx+c＝0，若b，c∈{0，1，2，3}，记“该方程有实数根x1，x2且满足﹣1≤x1≤x2≤2”为事件A，则事件A发生的概率为（　　）
A．14 B．34 C．78 D．1516
【分析】基本事件总数n＝4×4＝16．①当b＝0时，满足条件的基本事件有3个；②当b＝1时，满足条件的基本事件有4个；③当b＝2时，满足条件的基本事件有4个；④当b＝3时，满足条件的基本事件有3个．由此能求出事件A发生的概率．
【解答】解：基本事件总数n＝4×4＝16．
①当b＝0时，
c＝0，2x2＝0成立；c＝1，2x2＝1，成立；c＝2，2x2＝2，成立；
c＝3，2x2＝3，不成立．
满足条件的基本事件有3个；
②当b＝1时，
c＝0，2x2﹣x＝0，成立；c＝1，2x2﹣x＝1，成立；c＝2，2x2﹣x﹣2＝0，成立；
c＝3，2x2﹣x﹣3＝0，成立．
满足条件的基本事件有4个；
③当b＝2时，
c＝0，2x2﹣2x＝0，成立；c＝1，2x2﹣2x﹣1＝0，成立；c＝2，2x2﹣2x﹣2＝0，成立；
c＝3，2x2﹣2x﹣3＝0，成立．
满足条件的基本事件有4个；
④当b＝3时，
c＝0，2x2﹣3x＝0，成立；c＝1，2x2﹣3x﹣1＝0，成立；c＝2，2x2﹣3x﹣2＝0，成立；
c＝3，2x2﹣3x﹣3＝0，不成立．
满足条件的基本事件有3个．
∴满足条件的基本事件共有：3+4+4+3＝14个．
∴事件A发生的概率为p=1416=78．
故选：C．
5．甲袋中装有白球3个，黑球5个，乙袋内装有白球4个，黑球6个．现从甲袋内随机抽取一个球放入乙袋，充分掺混后再从乙袋内随机抽取一球放入甲袋，则甲袋中的白球没有减少的概率为（　　）
A．3714 B．3544 C．2544 D．544
【分析】甲袋中白球没有减少的两种情形；一是从甲袋中取出的球为黑球，此时不论从乙袋中取何种球放回甲袋，甲袋中的白球不会减少，另一种情形为从甲袋中取出的球是白球，放入乙袋，并由乙袋取白球放入甲．
【解答】解：甲袋中白球没有减少的两种情形；一是从甲袋中取出的球为黑球，记作事件E，
此时不论从乙袋中取何种球放回甲袋，甲袋中的白球不会减少，
另一种情形为从甲袋中取出的球是白球，放入乙袋，此事件用F1表示，
并由乙袋取白球放入甲，用F2表示，
令F＝F1F2．
则所求事件为E∪F，且E与F互斥，
显然P（E）=58，
下面计算P（F），记F1为由甲袋取出白球（不放入乙袋），
F2为当乙袋内有5个白球，6个黑球时取出一球为白球，
则显然有P（F1F2）＝P（F1′F2′）．
而F1′与F2′独立，故P（F1′F2′）=38•511．
∴P（E∪F）＝P（E）+P（F）=58+38•511=3544
故选：B．
6．从数字1，2，3，4，5这五个数中，随机抽取2个不同的数，则这2个数的和为偶数的概率是（　　）
A．15 B．25 C．35 D．45
【分析】由题意知本题是一个古典概型，本实验的总事件是从五个数中随机抽取2个不同的数有C52种不同的结果，满足条件的事件是这2个数的和为偶数包括2、4，1、3，1、5，3、5，四种取法，代入公式得到结果．
【解答】解：由题意知本题是一个古典概型，
∵从五个数中随机抽取2个不同的数有C52种不同的结果，
而这2个数的和为偶数包括2、4，1、3，1、5，3、5，四种取法，
由古典概型公式得到P=4C52=410=25，
故选：B．
7．某校3名教师和5名学生共8人去北京参加学习方法研讨会，需乘坐两辆车，每车坐4人，则恰有两名教师在同一车上的概率（　　）
A．13 B．37 C．67 D．56
【分析】首先计算8人乘坐两辆车，每车坐4人的情况数目，具体为：在8个人中取出4人，坐第一辆车，剩下的坐第二辆车，由组合数公式计算可得其情况数目；再计算恰有两名教师在同一车上的情况数目，具体为：先在3名教师中任取两人，5名学生中取两人构成第一组，乘坐第一辆车，剩下的构成第二组，乘坐第二辆车，由组合数公式可得其情况数目；由等可能事件的概率计算可得答案．
【解答】解：根据题意，要满足8人乘坐两辆车，每车坐4人，
可在8个人中取出4人，坐第一辆车，剩下的坐第二辆车，则有C84＝70种情况；
要满足恰有两名教师在同一车上，可先在3名教师中任取两人，5名学生中取两人构成第一组，乘坐第一辆车，剩下的构成第二组，乘坐第二辆车，则有C32×C52种分组方法，
再对应到两辆车，共有2C32×C52＝60种乘坐方法；
则恰有两名教师在同一车上的概率为6070=67；
故选：C．
8．如图是一个正方体纸盒的展开图，把1，1，2，2，3，3分别填入小正方形后，按虚线折成正方体，则所得到的正方中体相对面上的两个数都相等的概率是（　　）

A．415 B．16 C．115 D．120
【分析】先将6个数字在图中6个位置全排列，由排列数公式可得其情况数目，结合等差数列的性质分析可得，要使正方体相对面上两个数的和都相等，必须是1、1相对，2、2相对，3、3相对；由组合数公式分析可得正方体两个对面上两数字和相等的组合方式，由等可能事件的概率公式计算可得答案．
【解答】解：由题意，图中有6个位置，将1，1，2，2，3，3这6个数字在6个位置全排列，共有A66种结果，
要使所得到的正方中体相对面上的两个数都相等都相等，必须是1、1相对，2、2相对，3、3相对，
正方体有6个面，写第一个数字时有6种选择，
剩下四个面，则第三个数字只有4种选择，
此时剩余两个面，2个数字，有2种选择；
以此类推，可得出正方体两个对面上两数字和相等的组合方式有6×4×2＝48．
∴所得到的正方中体相对面上的两个数都相等的概率为：
P=48A66=115．
故选：C．
9．如图是一块高尔顿板示意图：在一块木板上钉着若干排互相平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，小球从上方的通道口落下后，将与层层小木块碰撞，最后掉入下方的某一个球槽内．若小球下落过程中向左、向右落下的机会均等，则小球最终落③号球槽的概率为（　　）

A．332 B．1564 C．532 D．516
【分析】用小球落入③球槽的种数除以小球落入下方的各个球槽的种数即可求得概率．
【解答】解：由题可知：小球落入③号球槽有C52=10种情况，小球落入下方球槽共有25＝32，
∴小球最终落③号球槽的概率为1032=516．
故选：D．
10．在简单随机抽样中，某一个个体被抽中的可能性是（　　）
A．与第几次抽样无关，每次抽中的可能性都相等
B．与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能性不一样
C．第1次抽中的可能性要大于第2次，第2次抽中的可能性要大于第3次，……，以此类推
D．第1次抽中的可能性要小于第2次，第2次抽中的可能性要小于第3次，……，以此类推
【分析】在简单随机抽样中从n个样品中抽取一个，不论先后，每个样品被抽到的概率都是1n．
【解答】解：在简单随机抽样中，
从n个样品中抽取一个，不论先后，每个样品被抽到的概率都是1n，
∴某一个个体被抽中的可能性是与第几次抽样无关，每次抽中的可能性都相等．
故选：A．
11．甲、乙两人下棋，和棋概率为12，乙获胜概率为13，甲获胜概率是（　　）
A．12 B．13 C．16 D．23
【分析】由于甲获胜与两个人和棋或乙获胜成立；甲获胜概率等于1减去和棋概率再减去乙获胜概率即可．
【解答】解：甲获胜概率是1−12−13=16
故选：C．
12．从(3x+1x)10的展开式中任选一项，使选出的项中x的幂指数为整数的概率为（　　）
A．111 B．211 C．311 D．411
【分析】利用二项展开式的通项公式求出展开式的通项，令x的指数为整数，即r为3的倍数，求出满足条件的r的个数即可．
【解答】解：展开式共有11项
(3x+1x)10的展开式的通项为
Tr+1=C10rx10−4r3
令10−4r3为整数得到r＝1，4，7，10
即选出的项中x的幂指数为整数的共有4项
所以选出的项中x的幂指数为整数的概率为411
故选：D．
13．某项试验的成功率是失败率的2倍，用随机变量ξ描述一次试验成功的次数，则P（ξ＝0）等于（　　）
A．0 B．12 C．13 D．23
【分析】本题考查的知识点是等可能事件的概率，由该项试验的结果只有成功和失败两种可能，故实验成功和实验失败为对立事件，即P（ξ＝1）+P（ξ＝0）＝1，又由试验的成功率是失败率的2倍，故P（ξ＝1）＝2P（ξ＝0），解方程组即可得到P（ξ＝0）的值．
【解答】解：由题意知，“ξ＝0”表示试验失败，“ξ＝1”表示试验成功．
则P（ξ＝1）＝2P（ξ＝0）
又P（ξ＝1）+P（ξ＝0）＝1，
∴P（ξ＝0）=13．
故选：C．
14．古代数学名著《九章算术》有“米谷粒分”题：粮仓开仓收粮，有人送来米2016石，验得米内夹谷，抽样取米一把，数得270粒内夹谷30粒，则这批米内夹谷约为（　　）
A．222石 B．224石 C．230石 D．232石
【分析】设这批米内夹谷约为x石，利用等可能事件概率计算公式能求出结果．
【解答】解：粮仓开仓收粮，有人送来米2016石，验得米内夹谷，
抽样取米一把，数得270粒内夹谷30粒，
设这批米内夹谷约为x石，
则x2016=30270，
解得x＝224（石）．
故选：B．
15．中共一大会址（现上海市兴业路76号）、江西井冈山（中共革命根据地）、贵州遵义（遵义会议召开地）、陕西延安（中共革命圣地）是中学生的几个重要的研学旅行地（只是部分）．某中学在校学生3000人，学校团委为了了解本校学生到上述红色基地研学旅行的情况，随机调查了500名学生，其中到过中共一大会址或井冈山研学旅行的共有40人，到过井冈山研学旅行的20人，到过中共一大会址并且到过井冈山研学旅行的恰有10人，根据这项调查，估计该学校到过中共一大会址研学旅行的学生大约有（　　）人．
A．240 B．180 C．120 D．60
【分析】先求出500人中符合条件的人数，再按对应比例相等即可求解．
【解答】解：因为500名学生中到过中共一大会址或井冈山研学旅行的共有40人，

到过井冈山研学旅行的20人，到过中共一大会址并且到过井冈山研学旅行的恰有10人；
故到过中共一大会址研学旅行的学生有30人；
所以：按照其所占比例可得：30500=所求3000⇒所求＝180；
故选：B．
16．从1，2，3，4这4个数中，不放回地任意取两个数，两个数都是奇数的概率是（　　）
A．16 B．14 C．13 D．12
【分析】根据已知中从1，2，3，4这4个数中，不放回地任意取两个数，我们列出所有的基本事件个数，及满足条件两个数都是奇数的基本事件个数，代入古典概型概率公式，即可得到答案．
【解答】解：从1，2，3，4这4个数中，不放回地任意取两个数，共有
（1，2），（1，3），（1，4），（2，1），（2，3），（2，4）
（3，1），（3，2），（3，4），（4，1），（4，2），（4，3）共12种
其中满足条件两个数都是奇数的有（1，3），（3，1）两种情况
故从1，2，3，4这4个数中，不放回地任意取两个数，两个数都是奇数的概率P=212=16
故选：A．
二．填空题（共14小题）
17．从4名男生和3名女生中选出4人去参加辩论比赛，则选出的4人中至少有2名男生的概率为　3135　．（用数字作答）
【分析】基本事件总数n=C74=35，选出的4人中至少有2名男生包含的基本事件个数为m=C42C32+C43C31+C44=31，由此能求出选出的4人中至少有2名男生的概率．
【解答】解：从4名男生和3名女生中选出4人去参加辩论比赛，
基本事件总数n=C74=35，
选出的4人中至少有2名男生包含的基本事件个数为：
m=C42C32+C43C31+C44=31，
则选出的4人中至少有2名男生的概率为p=mn=3135．
故答案为：3135．
18．如果生男孩和生女孩的概率相等，则有3个小孩的家庭中至少有2个女孩的概率是　0.5　．
【分析】利用列举法求出基本事件总数n＝8，其中至少有2个女孩包含的基本事件有4个，由此能求出有3个小孩的家庭中至少有2个女孩的概率．
【解答】解：生男孩和生女孩的概率相等，则有3个小孩的家庭中存在的基本事件有：
{男男男}，{男女女}，{女男女}，{女女男}，{男男女}，{男女男}，{女男男}，{女女女}，共8个，
其中至少有2个女孩包含的基本事件有4个，
故有3个小孩的家庭中至少有2个女孩的概率是P=48=12．
故答案为：12．
19．一个不透明的袋中装有5个白球、4个红球（9个球除颜色外其余完全相同），经充分混合后，从袋中随机摸出3球，则摸出的3球中至少有一个是白球的概率为　2021　．
【分析】总的基本事件数是9球中取3个，由组合数公式算出总的基本事件数即可，“3球中至少有一个是白球的”的对立事件是没有白球，应先计算其对立事件的概率，再求其概率．
【解答】解：由题意，总的基本事件数是9球中取3个，由组合数公式得，总的基本事件数是C93＝84种
3球中至少有一个是白球的”的对立事件是“没有白球”，
“没有白球”即取出的三个球都是红球，总的取法共有C43＝4种
故事件“没有白球”的概率是484=121
所以，“3球中至少有一个是白球的”的概率是1−121=2021
故答案为：2021
20．同时掷两粒骰子，则点数之和为7的概率是　16　．（结果用分数表示）
【分析】由题意知本题是一个古典概型，试验发生的所有事件为掷两颗骰子所有的6×6＝36种结果，而满足条件的事件通过列举得到结果为1，6；2，5；3，4；4，3；5，2；6，1共有6种结果，列举时要做到不重不漏．
【解答】解：由题意知本题是一个古典概型，
∵试验发生的所有事件为掷两颗骰子所有的6×6＝36种结果，
而满足条件的事件为1，6；2，5；3，4；4，3；5，2；6，1共有6种结果，
∴由古典概型公式得到结果P=636=16，
故答案为：16．
21．有编号分别为1，2，3，4，5的5个红球和5个黑球，从中随机取出4个，则取出球的编号互不相同的概率为　821　．
【分析】本题是一个古典概型，试验包含的总事件从10个球中取出4个，不同的取法有C104＝210种，再确定取出的球的编号互不相同的取法有C54•24＝80种，即可求出概率．
【解答】解：由题意，试验包含的总事件从10个球中取出4个，不同的取法有C104＝210种．
满足条件的如果要求取出的球的编号互不相同，可以先从5个编号中选取4个编号，有C54种选法．
对于每一个编号，再选择球，有两种颜色可供挑选，
∴取出的球的编号互不相同的取法有C54•24＝80种．
∴取出的球的编号互不相同的概率为80210=821．
故答案为：821．
22．我校2019级高一新生1800人．根据入校体验的视力数据库，我们抽取了50个样本，其中“视力不低于5.0”有27个．由此可以估计我校2019级高一新生中“视力不低于5.0”的比例约为　54%　．
【分析】直接根据50个样本，其中“视力不低于5.0”有27个即可求解结论．
【解答】解：∵抽取了50个样本，其中“视力不低于5.0”有27个；
∴可以估计我校2019级高一新生中“视力不低于5.0”的比例约为：2750=54%．
故答案为：54%．
23．古代“五行”学说认为：“物质分金、木、水、火、土五种属性，金克木、木克土，土克水，水克火，火克金”，从这五种不同属性的物质中随机抽取两种，则抽取的两种物质不相克的概率是　12　．
【分析】先求出五种抽出两种的抽法，再计算出相克的种数，由公式计算出答案．
【解答】解：五种抽出两种的抽法有C52＝10种
相克的种数有5种
故不相克的种数有5种
故五种不同属性的物质中随机抽取两种，则抽取的两种物质不相克的概率是12
故答案为12
24．某小组共有10名学生，其中女生3名，现选举2名代表，至少有1名女生当选的概率为　815　．
【分析】设“恰有一名女生当选”为事件A，“恰有两名女生当选”为事件B，显然A、B为互斥事件，利用互斥事件的概率公式即可求解．
【解答】解：设“恰有一名女生当选”为事件A，“恰有两名女生当选”为事件B，显然A、B为互斥事件．
从10名同学中任选2人共有10×9÷2＝45种选法（即45个基本事件），而事件A包括3×7个基本事件，事件B包括3×2÷2＝3个基本事件，故P＝P（A）+P（B）=2145+345=815
故答案为：815
25．玲玲和倩倩是一对好朋友，她俩都想去观看某歌星的演唱会，可手里只有一张票，怎么办呢？玲玲对倩倩说：“我向空中抛两枚同样的一元硬币，如果落地后一正一反，我就去，如果落地后两面一样，你就去！”这个办法　公平　.（选填“公平”或“不公平”）
【分析】分别求出玲玲和倩倩去的概率，由此能求出结果．
【解答】解：抛两枚同样的一元硬币，结果为正反，反正，正正，反反，
故一正一反的概率为12，两面一样的概率为12，
故这个办法公平，
故答案为：公平．
26．我国古代数学名著《九章算术》中有“米谷粒分”题：粮仓开仓收粮，有人送来米1536石，验得米内夹谷，抽样取米一把，数得256粒内夹谷18粒，则这批米内夹谷约为　108石　
【分析】设这批米内夹谷约为x石，利用等可能事件概率公式列出方程，由此能求出结果．
【解答】解：粮仓开仓收粮，有人送来米1536石，验得米内夹谷，
抽样取米一把，数得256粒内夹谷18粒，
设这批米内夹谷约为x石，
则x1536=18256，解得x＝108（石）．
∴这批米内夹谷约为108石．
故答案为：108石．
27．口袋内装有一些大小相同的红球、黄球和蓝球，从中摸出1个球，摸出红球的概率为0.42，摸出黄球的概率是0.28．若红球有21个，则蓝球有　15　个．
【分析】先求出摸出蓝球的概率是p＝1﹣0.42﹣0.28＝0.3，再由红球有21个，求出师口袋内装有一些大小相同的红球、黄球和蓝球总数为：210.42=50，由此能求出蓝球个数．
【解答】解：口袋内装有一些大小相同的红球、黄球和蓝球，
从中摸出1个球，摸出红球的概率为0.42，摸出黄球的概率是0.28．
∴摸出蓝球的概率是p＝1﹣0.42﹣0.28＝0.3，
∵红球有21个，
∴口袋内装有一些大小相同的红球、黄球和蓝球总数为：210.42=50，
∴蓝球有：50×0.3＝15．
故答案为：15．
28．在抛掷一颗骰子（一种正方体玩具，六个面标有1，2，3，4，5，6字样）的试验中，事件A表示“不大于4的偶数点出现”，事件B表示“小于5的点数出现”，则事件A+B的概率为　23　．
【分析】示出P（A）=13，P（B）=13，由A与B互斥，能求出事件A+B的概率．
【解答】解：在抛掷一颗骰子（一种正方体玩具，六个面标有1，2，3，4，5，6字样）的试验中，
事件A表示“不大于4的偶数点出现”，事件B表示“小于5的点数出现”，
则P（A）=26=13，P（B）=26=13，
A与B互斥，
∴事件A+B的概率为P（A+B）＝P（A）+P（B）=13+13=23．
故答案为：23．
29．为估计池塘中鱼的数量，负责人将50条带有标记的同品种鱼放入池塘，几天后，随机打捞40条鱼，其中带有标记的共5条．利用统计与概率知识可以估计池塘中原来有鱼　400　条．
【分析】设池塘中原来有鱼n条，则540=50n，由此能估计池塘中原来有鱼的数量．
【解答】解：为估计池塘中鱼的数量，负责人将50条带有标记的同品种鱼放入池塘，
几天后，随机打捞40条鱼，其中带有标记的共5条．
设池塘中原来有鱼n条，则540=50n，
解得n＝400．
故答案为：400．
30．口袋里有3个红球，2个白球，质地均匀，形状完全相同，从中任意摸出两个球，两个都是红球的概率　310　．
【分析】列树形图，列举出所有情况，看两个球都是红球的情况占所有情况的多少即可．
【解答】解：共有20种情况，两个都是红球的情况有6种，
所以概率是 310．
故答案为：310．

三．解答题（共8小题）
31．在10件产品中有一等品6件，二等品2件（一等品和二等品都是正品），其余为次品．
（Ⅰ）从中任取2件进行检测，2件都是一等品的概率是多少？
（Ⅱ）从中任取2件进行检测，2件中至少有一件次品的概率是多少？
（Ⅲ）如果对产品逐个进行检测，且已检测到前3次均为正品，则第4次检测的产品仍为正品的概率是多少？
【分析】（Ⅰ）先算出本题的等可能基本事件总数为45，事件A包含的基本事件数为15，从而可求出概率；
（Ⅱ）欲求2件中至少有一件次品的概率，先求2件中没有次品的概率，利用对立事件的概率求解即可；
（Ⅲ）欲求第4次检测的产品仍为正品的概率，就是求从含有5件正品，2件次品的7件产品中任取1件进行检测，抽到正品的概率．
【解答】解：
（Ⅰ）记事件A：2件都是一等品，本题的等可能基本事件总数为45，事件A包含的基本事件数为15，
所以P(A)=1545=13；（4分）
（Ⅱ）记事件B：2件中至少有一件次品，则事件B：2件中没有次品，事件B包含的基本事件数为28，
所以P(B)=2845
进而可得：P(B)=1−P(B)=1−2845=1745；（8分）
（Ⅲ）记事件C：第4次检测的产品仍为正品，
由于已检测到前3次均为正品，所以第4次检测就是从含有5件正品，
2件次品的7件产品中任取1件进行检测，所以P(C)=57．（12分）
32．某校从参加高二年级学业水平测试的学生中抽出80名学生，其数学成绩（均为整数）的频率分布直方图如图所示．
（Ⅰ）估计这次测试数学成绩的平均分；
（Ⅱ）假设在[90，100]段的学生的数学成绩都不相同，且都在94分以上，现用简单随机抽样的方法，从95，96，97，98，99，100这6个数中任取2个数，求这两个数恰好是在[90，100]段的两个学生的数学成绩的概率．

【分析】（Ⅰ）利用分组两端的数据中值估算抽样学生的平均分，类似于加权平均数的算法，让每一段的中值乘以这一段对应的频率，得到平均数，利用样本的平均数来估计总体的平均数．
（Ⅱ）由组合数计算从95，96，97，98，99，100中抽2个数的情况数目，再计算出成绩在[90，100]段的学生的人数，进而可得这两个数恰好是两个学生的数学成绩的数目，由等可能事件的概率公式，计算可得答案．
【解答】解：（Ⅰ）可以利用各组数据的中值估算抽样学生的平均分，
x=45×0.05+55×0.15+65×0.2+75×0.3+85×0.25+95×0.05＝72
所以，估计这次考试的平均分是72分．
（Ⅱ）从95，96，97，98，99，100中抽2个数的全部可能的基本结果数是C62＝15，有15种结果，
成绩在[90，100]段的学生的人数是0.005×10×80＝4人，
这两个数恰好是两个学生的数学成绩的基本结果数是C42＝6，
两个数恰好是两个学生的数学成绩的概率P=615=25．
33．将一枚质地均匀且四个面上分别标有1，2，3，4的正四面体先后抛掷两次，其底面落于桌面上，记第一次朝下面的数字为x，第二次朝下面的数字为y
（1）求满足条件“xy为整数”的事件的概率；
（2）求满足条件“x﹣y＜2”的事件的概率．
【分析】根据题意，可以用（x，y）来表示得到的点数情况，用列举法可得得到的点数的全部为整数”为事件A，分析列举的情况可得A包含的基本事件的个数，由等可能事件的概率的公式，计算可得答案；
（2）记“x﹣y＜2”为事件B，由列举的情况可得B包含的基本事件的个数，由等可能事件的概率的公式，计算可得答案．
【解答】解：根据题意，可以用（x，y）来表示得到的点数情况，
则得到的点数有（1，1）、（1，2）、（1，3）、（1，4）、（2，1）、（2，2）、（2，3）、（2，4）、（3，1）、（3，2）、（3，3）、（3，4）、（4，1）、（4，2）、（4，3）、（4，4），共16种情况；
（1）记“xy为整数”为事件A，则A包括（1，1）、（2，1）、（2，2）、（3，1）、（3，3）、（4，1）、（4，2）、（4，4），共8种情况，
则P（A）=816=12；
（2）记“x﹣y＜2”为事件B，则B包括（1，1）、（1，2）、（1，3）、（1，4）、（2，1）、（2，2）、（2，3）、（2，4）、（3，2）、（3，3）、（3，4）、（4，3）、（4，4），共13种情况；
则P（B）=1316．
34．某电子原件生产厂生产的10件产品中，有8件一级品，2件二级品，一级品和二级品在外观上没有区别．从这10件产品中任意抽检2件，计算：
（1）2件都是一级品的概率；
（2）至少有一件二级品的概率．
【分析】（1）本题是一个等可能事件的概率，从10件产品中抽取2件，共有C102个基本事件，而满足条件的事件的结果有C82，根据等可能事件的概率公式得到结果．
（2）至少有一件二级品包括抽取的2件产品中包含了一件一级品，一件二级品与抽取的2件产品均为二级品，这两种情况是互斥的，根据互斥事件的概率公式和等可能事件的概率公式得到结果．
【解答】解：（1）由题意知本题是一个等可能事件的概率，
设2件都是一级品为事件A．…（1分）
从10件产品中抽取2件，共有C102＝45个基本事件，且都是等可能的（2分）
而事件A的结果有C82＝28种，…（4分）
则P（A）=2845． …（5分）
（2）设至少有一件二级品为事件B，…（6分）
则B是两个互斥事件：“抽取的2件产品中包含了一件一级品，
一件二级品（记为B1）”与“抽取的2件产品均为二级品（B2）”的和． …（7分）
而P（B1）=1645，P（B2）=145，…（8分）
∴P（B）＝P（B1+B2）＝P（B1）+P（B2） …（10分）
=1645+145=1745． …（11分）
答：2件都是一级品的概率为2845；至少有一件二级品的概率为1745．（12分）
35．学生会6名同学，其中4名男同学2名女同学．现要从中随机选出2名代表发言．求：
（1）A同学被选中的概率是多少？
（2）至少有1名女同学被选中的概率是多少？
【分析】（1）根据所有的选法有C62种，而A同学被选中的方法有C11C51 种，故A同学被选中的概率是C51C62．
（2）所有的选法有C62种，至少有1名女同学包括两种情况：1个男同学与1个女同学，2个女同学，
分别有C41C21和C22 种选法，由此求得至少有1名女同学被选中的概率．
【解答】解：（1）所有的选法有C62种，A同学被选中的方法有C11C51 种，故A同学被选中的概率是 P=C51C62=13．
（2）所有的选法有C62种，至少有1名女同学包括两种情况：1个男同学与1个女同学，2个女同学，
这两种情况分别有C41C21和C22 种选法，
故至少有1名女同学被选中的概率是 P=C41C21+C22C62=35．
36．一个口袋内装有大小相同的5个球，3个白球，2个黑球，从中一次摸出两个球．
求：（1）共有多少个基本事件；
（2）摸出2个白球的概率．
【分析】（1）由题意知从5个球中摸出2个，共有C52个基本事件
（2）由题意知本题是一个等可能事件的概率，试验发生所包含的事件是从5个球中摸出2个，共有C52个基本事件，满足条件的事件是摸出两个白球，共有C32种结果，得到概率．
【解答】解：（1）由题意知从5个球中摸出2个，共有C52＝10个基本事件，
（2）由题意知本题是一个等可能事件的概率，
试验发生所包含的事件是从5个球中摸出2个，共有C52＝10个基本事件，
满足条件的事件是摸出两个白球，共有C32＝3种结果
∴满足条件的事件概率是310
答：从5个球中摸出2个共有10种结果，摸出两个白球的概率是310．
37．在一个池塘中有1000条鱼，其中有100条草鱼．现从中捕出20条鱼．试计算其中至少有两条草鱼的概率．
【分析】由已知可知X服从参数N＝1000，M＝100，n＝20的超几何分布，其分布列为P（X＝k）=C100kC90020−kC100020，（k＝0，1，…20），从而可求．
【解答】解：设X为扑出的20条鱼中草鱼的条数，则X可以取0，1，2…19，20；
则X服从参数N＝1000，M＝100，n＝20的超几何分布，其分布列为P（X＝k）=C100kC90020−kC100020，（k＝0，1，…20），
故20条鱼其中至少有两条草鱼的概率p＝1﹣P（X＝0）﹣P（X＝1）≈0.611．
38．袋子中装有编号为A1，A2，A3的3个黑球和编号为B1，B2的2个红球，从中任意摸出2个球．
（1）写出所有不同的结果；
（2）求恰好摸出1个黑球和1个红球的概率；
（3）求至少摸出1个红球的概率．
【分析】（1）利用树图法写出所有基本事件；
（2）找出1个黑球和1个红球的基本事件，利用概率公式计算；
（3）找出1个红球1个黑球和2个红球的基本事件，利用概率公式计算．
【解答】解：（1）从5个球中任意摸出2个球，有A1A2，A1A3，A2A3，A1B1，A1B2，A2B1，A2B2，A3B1，A3B2，B1B2共10种情况；
（2）记“恰好摸出1个黑球和1个红球”为事件A，
则事件A包含的基本事件为A1B1，A1B2，A2B1，A2B2，A3B1，A3B2，共6个基本事件．
所以P(A)=610=0.6；
（3）记“至少摸出1个红球”为事件B，则事件B包含的基本事件为A1B1，A1B2，A2B1，A2B2，A3B1，A3B2，B1B2，共7个基本事件，
所以P(B)=710=0.7．