人教版2022届一轮复习打地基练习 分布和频率分布表

这是一份人教版2022届一轮复习打地基练习 分布和频率分布表，共23页。试卷主要包含了一般地，家庭用电量等内容，欢迎下载使用。
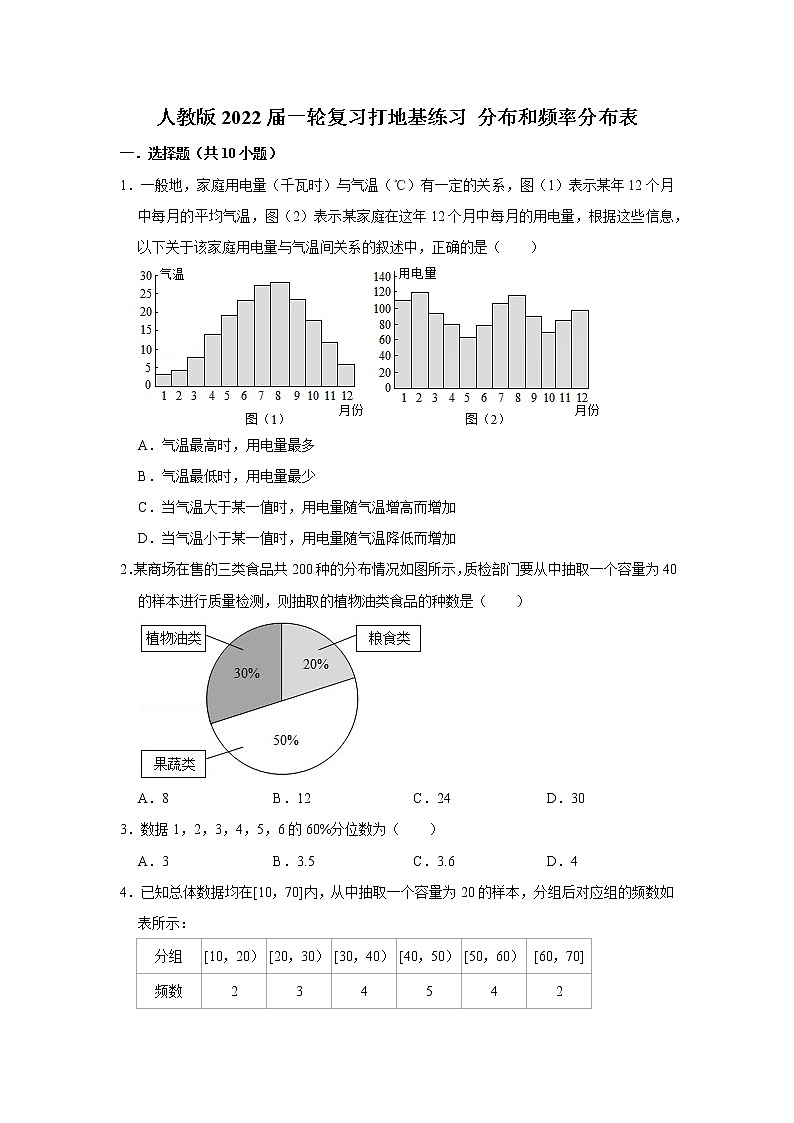
1．一般地，家庭用电量（千瓦时）与气温（℃）有一定的关系，图（1）表示某年12个月中每月的平均气温，图（2）表示某家庭在这年12个月中每月的用电量，根据这些信息，以下关于该家庭用电量与气温间关系的叙述中，正确的是（ ）
A．气温最高时，用电量最多
B．气温最低时，用电量最少
C．当气温大于某一值时，用电量随气温增高而增加
D．当气温小于某一值时，用电量随气温降低而增加
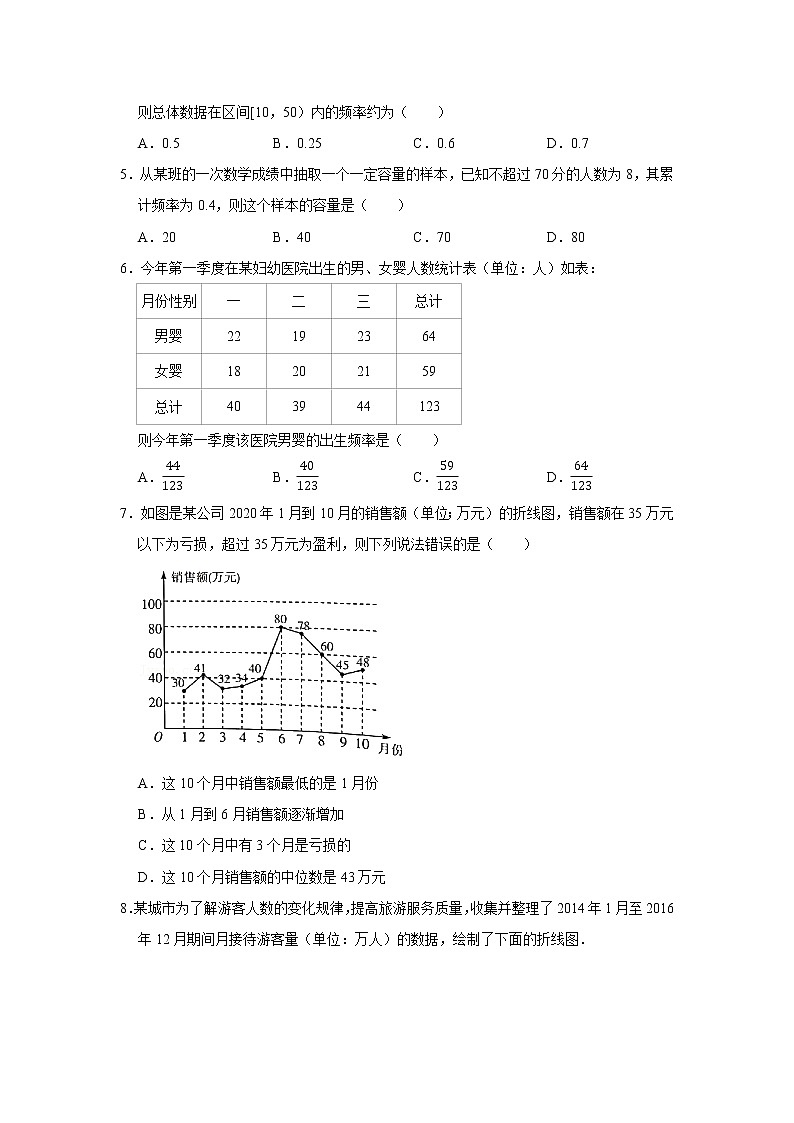
2．某商场在售的三类食品共200种的分布情况如图所示，质检部门要从中抽取一个容量为40的样本进行质量检测，则抽取的植物油类食品的种数是（ ）
A．8B．12C．24D．30
3．数据1，2，3，4，5，6的60%分位数为（ ）
A．3B．3.5C．3.6D．4
4．已知总体数据均在[10，70]内，从中抽取一个容量为20的样本，分组后对应组的频数如表所示：
则总体数据在区间[10，50）内的频率约为（ ）
A．0.5B．0.25C．0.6D．0.7
5．从某班的一次数学成绩中抽取一个一定容量的样本，已知不超过70分的人数为8，其累计频率为0.4，则这个样本的容量是（ ）
A．20B．40C．70D．80
6．今年第一季度在某妇幼医院出生的男、女婴人数统计表（单位：人）如表：
则今年第一季度该医院男婴的出生频率是（ ）
A．44123B．40123C．59123D．64123
7．如图是某公司2020年1月到10月的销售额（单位；万元）的折线图，销售额在35万元以下为亏损，超过35万元为盈利，则下列说法错误的是（ ）
A．这10个月中销售额最低的是1月份
B．从1月到6月销售额逐渐增加
C．这10个月中有3个月是亏损的
D．这10个月销售额的中位数是43万元
8．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．
根据该折线图，下列结论错误的是（ ）
A．年接待游客量逐年增加
B．月接待游客量逐月增加
C．各年的月接待游客量高峰期大致在 7，8 月
D．各年 1 月至 6 月的月接待游客量相对于 7 月至 12 月，波动性更小，变化比较平稳
9．一个样本容量为50的样本数据分组如下：[10，20），[20，30），[30，40），[40，50），[50，60]，其中样本数据在[10，20）和[40，50）内的频率之和为0.7，[20，30），[30，40）对应的频数分别为4，5，则样本数据在[50，60]内的频数为（ ）
A．4B．6C．11D．21
10．张家界市为创建文明城市，试进行生活垃圾分类处理，将生活垃圾分为厨余垃圾、可回收垃圾和其他垃圾三类，分别记为a，b，c．设置了厨余垃圾箱、可回收垃圾箱和其他垃圾箱，分别为A，B，C．为调查居民生活垃圾分类投放情况，随机抽取某小区三类垃圾箱中共计500kg生活垃圾，数据统计如表，则估计生活垃圾投放错误的概率为（ ）
A．2350B．16C．950D．310
二．填空题（共3小题）
11．某工厂对一批产品的净重（单位：克）进行抽样调查得到样本数据：230，235，237，238，238，239，240，242，244，246，据此估计这批产品的第80百分位数为 ．
12．抽取样本容量为20的样本数据，分组后的频数如表：
则样本数据落在区间[10，30）的频率为 ．
13．一个频率分布表（样本容量为50）不小心被损坏了一部分，只记得样本中数据在[20，60）上的频率为0.6，则估计样本在[40，50），[50，60）内的数据个数之和是 ．
三．解答题（共8小题）
14．某大型超市抽查了100天该超市的日纯利润数据，并将日纯利润数据分成以下几组（单位：万元）：[4，5），[5，6），[6，7），[7，8），[8，9），[9，10]，统计结果如表所示：
（1）求这100天该大型超市日纯利润的平均数及中位数；
（2）该大型超市负责人决定利用分层抽样的方法从前2组中随机抽出5天数据分析日纯利润较少的原因，并从这5天数据中再抽出其中2天数据进行深入分析，求这2天的数据恰好来自不同组的概率；
（3）利用上述样本分布估计总体分布，解决下面问题：
该大型超市总经理根据每天的纯利润给员工制定了两种奖励方案：
方案一：记日纯利润为x万元，当x＜6时，奖励每位员工40元/天，当6≤x＜8时，奖励每位员工80元/天；当x≥8时，奖励每位员工120元/天；
方案二：日纯利润低于总体中位数时每名员工发放奖金50元/天，日纯利润不低于总体中位数时每名员工发放80元奖金/天；
小张恰好为该大型超市的一位员工，则从统计角度看，小张选择哪种奖励方案更有利？
15．某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下左图所示．
（1）请先求出频率分布表中①、②位置相应的数据；
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试．
16．某校想了解高二数学成绩在学业水平考试中的情况，从中随机抽出50人的数学成绩作为样本并进行统计，频率分布表如表所示．
（1）据此估计这次参加数学考试的高二学生的数学平均成绩；
（2）从这五组中抽取14人进行座谈，若抽取的这14人中，恰好有2人成绩为50分，7人成绩为70分，2人成绩为75分，3人成绩为80分，求这14人数学成绩的方差；
（3）从50人的样本中，随机抽取测试成绩在[50，60]∪（90，100]内的两名学生，设其测试成绩分别为M，N．
（i）求事件“|M﹣N|＞30”的概率；
（ii）求事件“MN≤3600”的概率．
17．已知某大学有男生14000人，女生10000人，大学行政主管部门想了解该大学学生的运动状况，按性别采取分层抽样的方法从全校学生中抽取120人，统计他们平均每天运动的时间（单位：小时）如表：
（1）求实数x，y的值；
（2）若从被抽取的120人平均每天运动时间（单位：小时）在范围[0，0.5）的人中随机抽取2人，求“被抽取的2人性别不相同”的概率．
18．某城市缺水问题比较严重，市政府计划对居民生活用水费用实施阶梯式水价，为了解家庭用水量的情况，相关部分在某区随机调查了100户居民的月平均用水量（单位：t），得到如下频率分布表：
（1）求表中x，y，z的值；
（2）试估计该区居民的月平均用水量；
（3）从上表月平均用水量不少于22.5t的5户居民中随机抽取2户调查，求2户居民来自不同分组的概率．
19．2016年某省人社厅推出15项改革措施，包括机关事业单位基本养老保险制度改革、调整机关事业单位工资标准、全省县以下机关建立职务与职级并行制度．某市为了了解该市市民对这些改革措施的态度，在该市随机抽取了50名市民进行调查，作出了他们月收入（单位：百元，范围：[15，75]）的频率分布直方图，同时得到其中各种月收入情况的市民对该项政策赞成的人数统计表．
（1）求月收入在百元内的频率，并补全这个频率分布直方图，在图中标出相应的纵坐标；
（2）根据频率分布直方图估计这50人的平均月收入；
（3）为了这个改革方案能够更好的实施，从这些调查者中选取代表提供建议，若从月收入在[35，45）百元和[65，75]百元的不赞成的被调查者中随机抽取2人，求这两名代表月收入差不超过1000元的概率．
20．某射击选手在同一条件下进行射击，结果如表：
（Ⅰ）计算表中击中靶心的频率；
（Ⅱ）这名选手射击一次，击中靶心的概率是多少（保留小数点后两位数字）．
21．依托碳减排，中国发现了新的经济增长点，并实现经济增长引擎的转换，让中国成为全球最具潜力的“碳减排”市场．据统计，2019年全球某100个国家的碳排放减少量（单位：亿吨）数据分组如表：
（1）求m，n的值，并求碳排放减少量不小于1.42亿吨的概率；
（2）在统计方法中，同一组数据常用该组区间的中点值作为代表．据此估计这100个国家碳排放减少量的平均值（结果精确到0.01）．
（参考数据：1.36×0.16+1.44×0.24+1.52×0.08＝0.6848）
人教版2022届一轮复习打地基练习 分布和频率分布表
参考答案与试题解析
一．选择题（共10小题）
1．一般地，家庭用电量（千瓦时）与气温（℃）有一定的关系，图（1）表示某年12个月中每月的平均气温，图（2）表示某家庭在这年12个月中每月的用电量，根据这些信息，以下关于该家庭用电量与气温间关系的叙述中，正确的是（ ）
A．气温最高时，用电量最多
B．气温最低时，用电量最少
C．当气温大于某一值时，用电量随气温增高而增加
D．当气温小于某一值时，用电量随气温降低而增加
【分析】根据所给的两个图，可以看出在气温比较低的1，2月份，用电量很高，到4，5月份，气温适中，这时用电量最少，到7，8月份，气温是一年中最高的时候，8月份，气温和用电量都达到最高值，得到结论．
【解答】解：根据所给的两个图，可以看出在气温比较低的1，2月份，用电量很高，
到4，5月份，气温适中，这时用电量最少，
到7，8月份，气温是一年中最高的时候，这时，用电量最大，
8月份，气温和用电量都达到最高值，
即当气温大于某一值时，用电量随气温增高而增加，
故选：C．
2．某商场在售的三类食品共200种的分布情况如图所示，质检部门要从中抽取一个容量为40的样本进行质量检测，则抽取的植物油类食品的种数是（ ）
A．8B．12C．24D．30
【分析】由题意知利用分层抽样法，计算需要抽取的频数即可．
【解答】解：由题意知，利用分层抽样方法从中抽取容量为40的样本，
需要抽取的植物油类食品种数是40×30%＝12（种）．
故选：B．
3．数据1，2，3，4，5，6的60%分位数为（ ）
A．3B．3.5C．3.6D．4
【分析】根据一组数据的百分位数定义，求出对应的数值即可．
【解答】解：由（6﹣1）×60%＝3，
所以数据1，2，3，4，5，6的60%分位数是第4个数，为4．
故选：D．
4．已知总体数据均在[10，70]内，从中抽取一个容量为20的样本，分组后对应组的频数如表所示：
则总体数据在区间[10，50）内的频率约为（ ）
A．0.5B．0.25C．0.6D．0.7
【分析】计算样本数据在区间[10，50）内的频率即可．
【解答】解：利用样本估计总体知，
总体数据在区间[10，50）内的频率约为：
1−4+220=0.7．
故选：D．
5．从某班的一次数学成绩中抽取一个一定容量的样本，已知不超过70分的人数为8，其累计频率为0.4，则这个样本的容量是（ ）
A．20B．40C．70D．80
【分析】根据已知中的不超过70分的人的累计频率，结合频率＝矩形高×组距=频数样本容量，得到答案．
【解答】解：由已知中的频率分布直方图可得时间不超过70分的累计频率的频率为0.4，
则这样的样本容量是n=80.4=20．
故选：A．
6．今年第一季度在某妇幼医院出生的男、女婴人数统计表（单位：人）如表：
则今年第一季度该医院男婴的出生频率是（ ）
A．44123B．40123C．59123D．64123
【分析】直接利用已知条件的应用利用第一季度的男婴数为64，婴儿总数为123，求出男婴的出生频率．
【解答】解：根据题意：第一季度的男婴数为64，婴儿总数为123，
故该医院生男婴的出生频率为64123．
故选：D．
7．如图是某公司2020年1月到10月的销售额（单位；万元）的折线图，销售额在35万元以下为亏损，超过35万元为盈利，则下列说法错误的是（ ）
A．这10个月中销售额最低的是1月份
B．从1月到6月销售额逐渐增加
C．这10个月中有3个月是亏损的
D．这10个月销售额的中位数是43万元
【分析】通过理解折线图，即可得出答案．
【解答】解：根据折线图知，这个10月中销售额最低的是1月份，为30万元，所以A正确；
从1月到6月销售额是先增加后减少，再增加，所以B错误；
1月，3月和4月的销售额低于35万元，所以C正确；
这10个月的销售额从小到大排列为30，32，34，40，41，45，48，60，78，80万元，
其中位数是12×(41+45)=43万元，所以D正确．
故选：B．
8．某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．
根据该折线图，下列结论错误的是（ ）
A．年接待游客量逐年增加
B．月接待游客量逐月增加
C．各年的月接待游客量高峰期大致在 7，8 月
D．各年 1 月至 6 月的月接待游客量相对于 7 月至 12 月，波动性更小，变化比较平稳
【分析】由拆线图得到：月接待游客量8月份后逐月减少．
【解答】解：由折线图得：
在A中，年接待游客量逐年增加，故A正确；
在B中，月接待游客量8月份后逐月减少，故B错误；
在C中，各年的月接待游客量高峰期大致在 7，8 月，故C正确；
在D中，各年 1 月至 6 月的月接待游客量相对于 7 月至 12 月，波动性更小，变化比较平稳，故D正确．
故选：B．
9．一个样本容量为50的样本数据分组如下：[10，20），[20，30），[30，40），[40，50），[50，60]，其中样本数据在[10，20）和[40，50）内的频率之和为0.7，[20，30），[30，40）对应的频数分别为4，5，则样本数据在[50，60]内的频数为（ ）
A．4B．6C．11D．21
【分析】由样本数据在[10，20）和[40，50）内的频率之和为0.7，可得样本数据在[10，20）和[40，50）内的人数，
再结合[20，30），[30，40）对应的频数分别为4，5，即可求解．
【解答】解：∵样本数据在[10，20）和[40，50）内的频率之和为0.7，
∴样本数据在[10，20）和[40，50）内的人数为0.7×50＝35，
又∵[20，30），[30，40）对应的频数分别为4，5，
∴样本数据在[50，60]内的频数为50﹣35﹣5﹣4＝6．
故选：B．
10．张家界市为创建文明城市，试进行生活垃圾分类处理，将生活垃圾分为厨余垃圾、可回收垃圾和其他垃圾三类，分别记为a，b，c．设置了厨余垃圾箱、可回收垃圾箱和其他垃圾箱，分别为A，B，C．为调查居民生活垃圾分类投放情况，随机抽取某小区三类垃圾箱中共计500kg生活垃圾，数据统计如表，则估计生活垃圾投放错误的概率为（ ）
A．2350B．16C．950D．310
【分析】由数据统计表利用古典概型能估计生活垃圾投放错误的概率．
【解答】解：由数据统计表估计生活垃圾投放错误的概率为：
P=10+40+15+20+15+50500=310．
故选：D．
二．填空题（共3小题）
11．某工厂对一批产品的净重（单位：克）进行抽样调查得到样本数据：230，235，237，238，238，239，240，242，244，246，据此估计这批产品的第80百分位数为 243 ．
【分析】把数据从小到大排序，找到第8个、第9个数据，计算平均数．
【解答】解：共10个数，所以第80百分位数为第8个、第9个数据的平均数．
即242，244的平均数，计算得243．
故答案为：243．
12．抽取样本容量为20的样本数据，分组后的频数如表：
则样本数据落在区间[10，30）的频率为 0.25 ．
【分析】由频数表先求出样本数据落在区间[10，30）的频数，由此能求出样本数据落在区间[10，30）的频率．
【解答】解：由容量为20的样本数据，分组后的频数表得：
样本数据落在区间[10，30）的频数为2+3＝5，
∴样本数据落在区间[10，30）的频率为p=520=0.25．
故答案为：0.25．
13．一个频率分布表（样本容量为50）不小心被损坏了一部分，只记得样本中数据在[20，60）上的频率为0.6，则估计样本在[40，50），[50，60）内的数据个数之和是 21 ．
【分析】设分布在「40，50），[50，60）内的数据个数分别为x，y．根据样本容量为50和数据在[20，60）上的频率为0.6，建立关于x、y的方程，解之即可得到x+y的值．
【解答】解：根据题意，设分布在「40，50），[50，60）内的数据个数分别为x，y
∵样本中数据在[20，60）上的频率为0.6，样本容量为50
∴4+5+x+y50=0.6，解之得x+y＝21
即样本在「40，50），[50，60）内的数据个数之和为21
故答案为：21
三．解答题（共8小题）
14．某大型超市抽查了100天该超市的日纯利润数据，并将日纯利润数据分成以下几组（单位：万元）：[4，5），[5，6），[6，7），[7，8），[8，9），[9，10]，统计结果如表所示：
（1）求这100天该大型超市日纯利润的平均数及中位数；
（2）该大型超市负责人决定利用分层抽样的方法从前2组中随机抽出5天数据分析日纯利润较少的原因，并从这5天数据中再抽出其中2天数据进行深入分析，求这2天的数据恰好来自不同组的概率；
（3）利用上述样本分布估计总体分布，解决下面问题：
该大型超市总经理根据每天的纯利润给员工制定了两种奖励方案：
方案一：记日纯利润为x万元，当x＜6时，奖励每位员工40元/天，当6≤x＜8时，奖励每位员工80元/天；当x≥8时，奖励每位员工120元/天；
方案二：日纯利润低于总体中位数时每名员工发放奖金50元/天，日纯利润不低于总体中位数时每名员工发放80元奖金/天；
小张恰好为该大型超市的一位员工，则从统计角度看，小张选择哪种奖励方案更有利？
【分析】（1）由样本数字特征及频率之和为0.5的关系估算出中位数即可．（2）列出基本事件，由古典概型可计算概率，（3）计算两种方案的平均数进行比较可得哪个方案有利．
【解答】解：（1）这100天该大型超市日纯利涧的平均数为：
x=1100（4.5×5+5.5×20+6.5×30+7.5×30+8.5×10+9.5×5）＝6.85（万元），
前2组频率之和为：0.05+0.20＝0.25＜0.5，前3组频率之和为：0.25+0.3＝0.55＞0.5，故中位数位于第3组；
设中位数为t则有（t﹣6）×0.3+0.25＝0.5
解得：t=416；
即这100天该大型超市日纯利润的中位数为416万元；
（2）由分层抽样知识可知，所抽取的5天数据中，来自于[4，5），[5，6）这2组的天数分别为1，4．
记来自于[4，5）的1天为a，来自于[5，6）的4天分别为b，c，d，e；
则从中抽取2天的数据的所有可能结果有：（a，b）（a，c），（a，d），（a，e），（b，c），（b，d），（b，e），（c，d），（c，e），（d，e），共10种
其中这2天的数据来自不同组的有：（a，b），（a，c）（a，d），（a，e）共4种；
故所求的概率为：P=410=25；
（3）设选择方案一时，小张每天的奖金为X元，
则X的可能取值为40，80，120，其对应的概率分别为0.25，0.6，0.15，
所以获得奖金的平均数x=40×0.25+80×0.6+120×0.15＝76（元）
设选择方案二时小张每天的奖金为Y元
则获得奖金的平均数Y=50×0.5+80×0.5＝65（元）
因为X＞Y
所以从统计角度看，小张选择方案一更有利．
15．某高校在2009年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下左图所示．
（1）请先求出频率分布表中①、②位置相应的数据；
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试．
【分析】（1）根据所给的第二组的频率，利用频率乘以样本容量，得到要求的频数，再根据所给的频数，利用频除以样本容量，得到要求的频率．
（2）因为在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生，而这三个小组共有60人，利用每一个小组在60人中所占的比例，乘以要抽取的人数，得到结果．
【解答】解：（1）由题意可知，第2组的频数为0.35×100＝35人，
第3组的频率为30100=0.3，
（2）∵第3、4、5组共有60名学生，
∴利用分层抽样在60名学生中抽取6名学生，
每组分别为：第3组：3060×6=3人，第4组：2060×6=2人，第5组：1060×6=1人，
∴第3、4、5组分别抽取3人、2人、1人．
16．某校想了解高二数学成绩在学业水平考试中的情况，从中随机抽出50人的数学成绩作为样本并进行统计，频率分布表如表所示．
（1）据此估计这次参加数学考试的高二学生的数学平均成绩；
（2）从这五组中抽取14人进行座谈，若抽取的这14人中，恰好有2人成绩为50分，7人成绩为70分，2人成绩为75分，3人成绩为80分，求这14人数学成绩的方差；
（3）从50人的样本中，随机抽取测试成绩在[50，60]∪（90，100]内的两名学生，设其测试成绩分别为M，N．
（i）求事件“|M﹣N|＞30”的概率；
（ii）求事件“MN≤3600”的概率．
【分析】（1）以每组的中间值为代表数据，该组的频率为权，加权平均即可得到这次参加数学考试的高二学生的数学平均成绩；
（2）求出这14人数学成绩的平均分x，代入方差公式即可求出这14人数学成绩的方差；
（3）（i）成绩在[50，60]内的人数有2人，设其成绩分别为x，y，在（90，100]内的人数有3人，设其成绩分别为a，b，c，根据M．N所在范围分类讨论列出基本事件的总数和满足“|M﹣N|＞30”包含的基本事件个数，即可得到概率．
（ii）由（i）知事件MN≤3600的基本事件只有（x，y）这一种，基本事件总数为10，代入古典概型的概率公式即可．
【解答】解：（1）先求得a为9，b为0.40．
估计高二学生的数学平均成绩为：55×0.04+65×0.18+75×0.4+85×0.32+95×0.06＝76.8．
（2）这14人数学成绩的平均分为：x=50×2+70×7+75×2+80×314=70，
∴这14人数学成绩的方差为：s2=114[2(50−70)2+7(70−70)2+2(75−70)2+3(80−70)2]=5757．
（3）（i）由频数分布表知，成绩在[50，60]内的人数有2人，设其成绩分别为x，y；
在（90，100]内的人数有3人，设其成绩分别为a，b，c，
若M，N∈[50，60]时，只有（x，y）一种情况；
若M，N∈（90，100]时，有（a，b），（b，c），（a，c）三种情况；
若M，N分别在[50，60]和（90，100]内时，有：
共6种情况，
∴基本事件总数为10种，
事件“|M﹣N|＞30”所包含的基本事件有6种，
∴P(|M−N|＞30)=610=35．
（ii）事件MN≤3600的基本事件只有（x，y）这一种，
∴P(MN≤3600)=110．
17．已知某大学有男生14000人，女生10000人，大学行政主管部门想了解该大学学生的运动状况，按性别采取分层抽样的方法从全校学生中抽取120人，统计他们平均每天运动的时间（单位：小时）如表：
（1）求实数x，y的值；
（2）若从被抽取的120人平均每天运动时间（单位：小时）在范围[0，0.5）的人中随机抽取2人，求“被抽取的2人性别不相同”的概率．
【分析】（1）利用分层抽样求出样本个数，再根据题意，求出x，y；
（2）根据古典概型求出即可．
【解答】解：（1）男生14000人，女生10000人，男数：女数＝7：5，
故男生抽取了120×712=70人，女生抽取了50人，由2+12+23+18+10+x＝70，x＝5，
5+12+18+10+3+y＝48+y＝50，y＝2；
（2）从被抽取的120人平均每天运动时间（单位：小时）在范围[0，0.5）的人中随机抽取2人，“被抽取的2人性别不相同”的事件为A，
共有7人，所以总共有21种选法，
性别不同的有10种选法，
故P（A）=1021．
18．某城市缺水问题比较严重，市政府计划对居民生活用水费用实施阶梯式水价，为了解家庭用水量的情况，相关部分在某区随机调查了100户居民的月平均用水量（单位：t），得到如下频率分布表：
（1）求表中x，y，z的值；
（2）试估计该区居民的月平均用水量；
（3）从上表月平均用水量不少于22.5t的5户居民中随机抽取2户调查，求2户居民来自不同分组的概率．
【分析】由频率＝频数÷总数，频数＝总数×频率进行求解．
平均数用每组数据的中点×频率的结果相加得到．
【解答】解：（1）由图表可知，[7.5，10.5）区间内，居民用水量的频率为0.16，
∴x＝100×0.16＝16．
则y＝100﹣（22+31+16+10+5+5+3+2）＝6，
∴频率z＝6÷100＝0.06．
（2）x=3×0.22+6×0.31+9×0.16+12×0.1+15×0.06+18×0.05+21×0.05+24×0.03+27×0.02＝9.27．
（3）C52=5×42×1=10，
∴从上表月平均用水量不少于22.5t的5户居民中随机抽取2户的基本事件共10件，
来自同一分组的可能事件共1+C32=4种，∴来自不同分组的可能事件共6种．
记事件A：2户居民来自不同分组，
则P（A）=610=35．
19．2016年某省人社厅推出15项改革措施，包括机关事业单位基本养老保险制度改革、调整机关事业单位工资标准、全省县以下机关建立职务与职级并行制度．某市为了了解该市市民对这些改革措施的态度，在该市随机抽取了50名市民进行调查，作出了他们月收入（单位：百元，范围：[15，75]）的频率分布直方图，同时得到其中各种月收入情况的市民对该项政策赞成的人数统计表．
（1）求月收入在百元内的频率，并补全这个频率分布直方图，在图中标出相应的纵坐标；
（2）根据频率分布直方图估计这50人的平均月收入；
（3）为了这个改革方案能够更好的实施，从这些调查者中选取代表提供建议，若从月收入在[35，45）百元和[65，75]百元的不赞成的被调查者中随机抽取2人，求这两名代表月收入差不超过1000元的概率．
【分析】（1）根据频率和为1，利用频率直方图的画法，补全即可；
（2）根据平均数的定义，求出平均数，并用样本估计总体即可；
（3）根据古典概型概率公式，分别列举出所有的基本事件，再找到满足条件的基本事件，计算概率值．
【解答】解：（1）月收入在百元内的频率为
1﹣0.01×10×3﹣0.02×10×2＝0.3；
由0.310=0.03，补全这个频率分布直方图，如图所示；
（2）由频率分布直方图，计算平均数为
20×0.1+30×0.2+40×0.3+50×0.2+60×0.1+70×0.1＝43（百元），
即这50人的平均月收入估计为4300元；
（3）[35，45）内的人数为15人，其中12人赞成，3人不赞成；
记不赞成的人为a，b，c，）；
[65，75]内的人数为5人，其中2人赞成，3人不赞成；
记不赞成的3人为x，y，z；
从不赞成的6人中任取2人，基本事件是：
ab，ac，ax，ay，az，bc，bx，by，bz，cx，cy，cz，xy，xz，yz共15种情况；
其中两代表月收入差不超过1000元的有ab，ac，bc，xy，xz，yz，共6种情况，
∴故这两代表月收入不超过1000元的概率是P=615=25．
20．某射击选手在同一条件下进行射击，结果如表：
（Ⅰ）计算表中击中靶心的频率；
（Ⅱ）这名选手射击一次，击中靶心的概率是多少（保留小数点后两位数字）．
【分析】（I）根据频率等于频数除以次数求出；（II）根据概率的定义求出．
【解答】解：（I）
（II）根据频率估计概率的定义得，概率为0.90．
21．依托碳减排，中国发现了新的经济增长点，并实现经济增长引擎的转换，让中国成为全球最具潜力的“碳减排”市场．据统计，2019年全球某100个国家的碳排放减少量（单位：亿吨）数据分组如表：
（1）求m，n的值，并求碳排放减少量不小于1.42亿吨的概率；
（2）在统计方法中，同一组数据常用该组区间的中点值作为代表．据此估计这100个国家碳排放减少量的平均值（结果精确到0.01）．
（参考数据：1.36×0.16+1.44×0.24+1.52×0.08＝0.6848）
【分析】（1）利用频率、频数、样本容量的关系求出m，利用频率之和为1求出n，计算碳排放减少量不小于1.42亿吨的频率即可；
（2）利用平均数的求解公式计算即可．
【解答】解：（1）由题意可知，m＝100×0.24＝24，n＝1﹣0.16﹣0.32﹣0.24﹣0.16﹣0.08＝0.04，
碳排放减少量不小于1.42亿吨的概率为0.24+＝0.48；
（2）由1.32×0.04+1.36×0.16+1.40×0.32+1.44×0.24+1.48×0.16+1.52×0.08＝1.4224≈1.42，
估计这100个国家碳排放减少量的平均值为1.42亿吨．分组
[10，20）
[20，30）
[30，40）
[40，50）
[50，60）
[60，70]
频数
2
3
4
5
4
2
月份性别
一
二
三
总计
男婴
22
19
23
64
女婴
18
20
21
59
总计
40
39
44
123
A
B
C
a
200kg
10kg
40kg
b
15kg
120kg
20kg
c
15kg
50kg
30kg
分组
[10，20）
[20，30）
[30，40）
[40，50）
[50，60）
[60，70）
频数
2
3
4
5
4
2
组别
[4，5）
[5，6）
[6，7）
[7，8）
[8，9）
[9，10]
频数
5
20
30
30
10
5
组号
分组
频数
频率
第1组
[160，165）
5
0.050
第2组
[165，170）
①
0.350
第3组
[170，175）
30
②
第4组
[175，180）
20
0.200
第5组
[180，185）
10
0.100
合计
100
1.00
组号
分组
频数
频率
第1组
[50，60]
2
0.04
第2组
（60，70]
a
0.18
第3组
（70，80]
20
b
第4组
（80，90]
16
0.32
第5组
（90，100]
3
0.06
合计
50
1.00
男生平均每天运动的时间
[0，0.5）
[0.5，1）
[1，1.5）
[1.5，2）
[2，2.5）
[2.5，3）
人数
2
12
23
18
10
x
女生平均每天运动的时间
[0，0.5）
[0.5，1）
[1，1.5）
[1.5，2）
[2，2.5）
[2.5，3）
人数
5
12
18
10
3
y
分组
频数
频率
[1.5，4.5）
22
0.22
[4.5，7.5）
31
0.31
[7.5，10.5）
x
0.16
[10.5，13.5）
10
0.10
[13.5，16.5）
y
z
[16.5，19.5）
5
0.05
[19.5，22.5）
5
0.05
[22.5，25.5）
3
0.03
[25.5，28.5）
2
0.02
合计
100
1
月收入
赞成人数
[15，25）
4
[25，35）
8
[35，45）
12
[45，55）
5
[55，65）
2
[65，75]
2
射击次数n
10
20
50
100
200
400
500
击中靶心的频数m
8
19
44
95
180
364
445
击中靶心的频率m/n
减少量：亿吨
国家个数
频率
[1.30，1.34）
n
[1.34，1.38）
0.16
[1.38，1.42）
32
[1.42，1.46）
m
0.24
[1.46，1.50）
16
[1.50，1.54）
0.08
合计
100
1
分组
[10，20）
[20，30）
[30，40）
[40，50）
[50，60）
[60，70]
频数
2
3
4
5
4
2
月份性别
一
二
三
总计
男婴
22
19
23
64
女婴
18
20
21
59
总计
40
39
44
123
A
B
C
a
200kg
10kg
40kg
b
15kg
120kg
20kg
c
15kg
50kg
30kg
分组
[10，20）
[20，30）
[30，40）
[40，50）
[50，60）
[60，70）
频数
2
3
4
5
4
2
组别
[4，5）
[5，6）
[6，7）
[7，8）
[8，9）
[9，10]
频数
5
20
30
30
10
5
组号
分组
频数
频率
第1组
[160，165）
5
0.050
第2组
[165，170）
①
0.350
第3组
[170，175）
30
②
第4组
[175，180）
20
0.200
第5组
[180，185）
10
0.100
合计
100
1.00
组号
分组
频数
频率
第1组
[50，60]
2
0.04
第2组
（60，70]
a
0.18
第3组
（70，80]
20
b
第4组
（80，90]
16
0.32
第5组
（90，100]
3
0.06
合计
50
1.00
a
b
c
x
（x，a）
（x，b）
（x，c）
y
（y，a）
（y，b）
（y，c）
男生平均每天运动的时间
[0，0.5）
[0.5，1）
[1，1.5）
[1.5，2）
[2，2.5）
[2.5，3）
人数
2
12
23
18
10
x
女生平均每天运动的时间
[0，0.5）
[0.5，1）
[1，1.5）
[1.5，2）
[2，2.5）
[2.5，3）
人数
5
12
18
10
3
y
分组
频数
频率
[1.5，4.5）
22
0.22
[4.5，7.5）
31
0.31
[7.5，10.5）
x
0.16
[10.5，13.5）
10
0.10
[13.5，16.5）
y
z
[16.5，19.5）
5
0.05
[19.5，22.5）
5
0.05
[22.5，25.5）
3
0.03
[25.5，28.5）
2
0.02
合计
100
1
月收入
赞成人数
[15，25）
4
[25，35）
8
[35，45）
12
[45，55）
5
[55，65）
2
[65，75]
2
射击次数n
10
20
50
100
200
400
500
击中靶心的频数m
8
19
44
95
180
364
445
击中靶心的频率m/n
射击次数n
10
20
50
100
200
400
500
击中靶心的频数m
8
19
44
95
180
364
445
击中靶心的频率m/n
0.8
0.95
0.88
0.95
0.9
0.91
0.89
减少量：亿吨
国家个数
频率
[1.30，1.34）
n
[1.34，1.38）
0.16
[1.38，1.42）
32
[1.42，1.46）
m
0.24
[1.46，1.50）
16
[1.50，1.54）
0.08
合计
100
1