人教版2022届一轮复习打地基练习 频率分布直方图

这是一份人教版2022届一轮复习打地基练习 频率分布直方图，共38页。

A．150B．250C．300D．400
2．某小区居民上网年龄分布图如图所示，现按照分层抽样的方法从该小区抽取一个容量为n的样本．若样本中90后比00后多52人，则n＝（ ）
A．400B．450C．500D．550
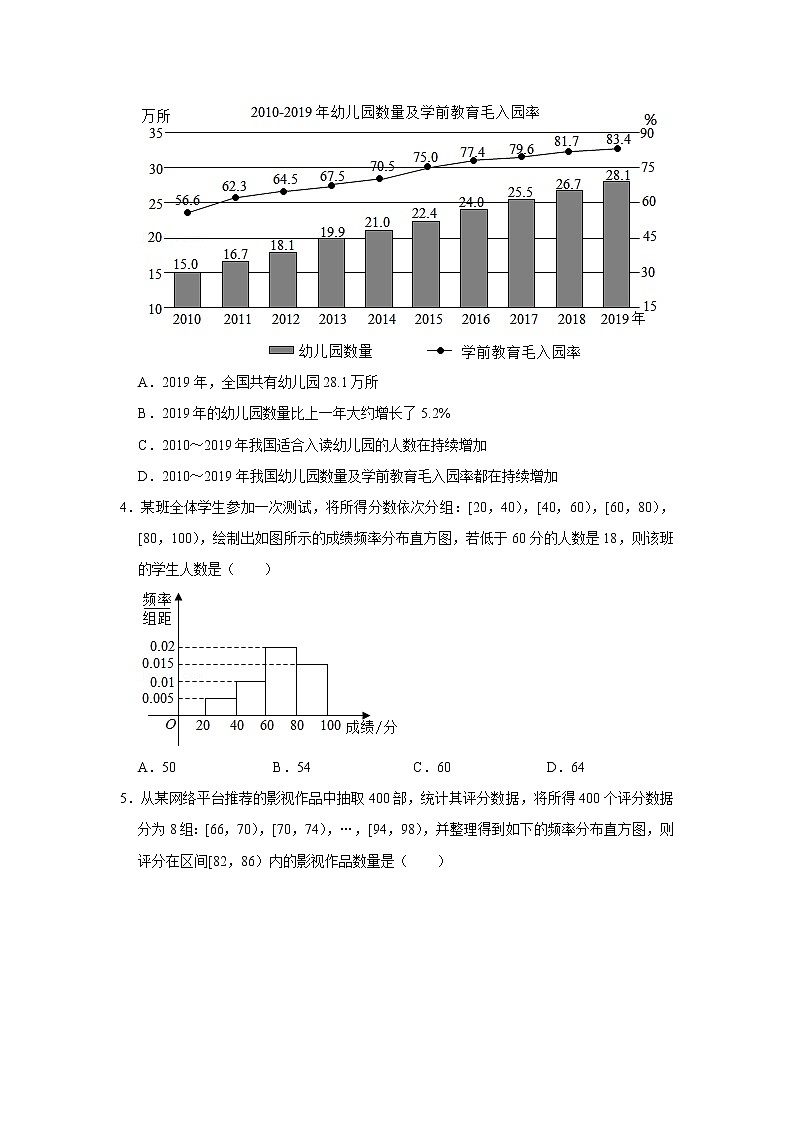
3．近年来，我国继续大力发展公办幼儿园，积极扶持普惠性民办幼儿园，使得普惠性学前教育资源迅速增加．如图为国家统计局发布的2010～2019年幼儿园数量及学前教育毛入园率统计图．根据该统计图，下列说法不一定正确的是（ ）
注：毛入园率=适龄儿童入读幼儿园人数适龄儿童总人数．
A．2019年，全国共有幼儿园28.1万所
B．2019年的幼儿园数量比上一年大约增长了5.2%
C．2010～2019年我国适合入读幼儿园的人数在持续增加
D．2010～2019年我国幼儿园数量及学前教育毛入园率都在持续增加
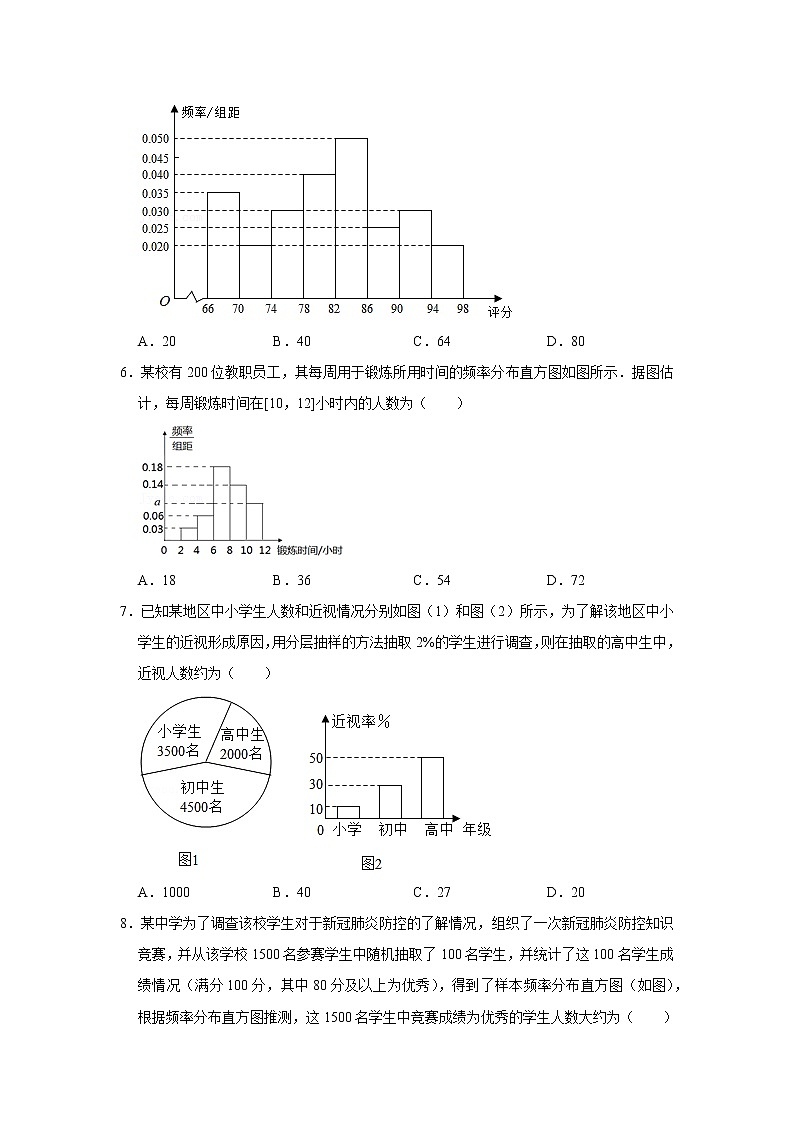
4．某班全体学生参加一次测试，将所得分数依次分组：[20，40），[40，60），[60，80），[80，100），绘制出如图所示的成绩频率分布直方图，若低于60分的人数是18，则该班的学生人数是（ ）
A．50B．54C．60D．64
5．从某网络平台推荐的影视作品中抽取400部，统计其评分数据，将所得400个评分数据分为8组：[66，70），[70，74），…，[94，98），并整理得到如下的频率分布直方图，则评分在区间[82，86）内的影视作品数量是（ ）
A．20B．40C．64D．80
6．某校有200位教职员工，其每周用于锻炼所用时间的频率分布直方图如图所示．据图估计，每周锻炼时间在[10，12]小时内的人数为（ ）
A．18B．36C．54D．72
7．已知某地区中小学生人数和近视情况分别如图（1）和图（2）所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则在抽取的高中生中，近视人数约为（ ）
A．1000B．40C．27D．20
8．某中学为了调查该校学生对于新冠肺炎防控的了解情况，组织了一次新冠肺炎防控知识竞赛，并从该学校1500名参赛学生中随机抽取了100名学生，并统计了这100名学生成绩情况（满分100分，其中80分及以上为优秀），得到了样本频率分布直方图（如图），根据频率分布直方图推测，这1500名学生中竞赛成绩为优秀的学生人数大约为（ ）
A．360B．420C．480D．540
二．填空题（共18小题）
9．某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100]．若低于60分的人数是6人，则参加该英语测试的学生人数是 ．
10．某校100名学生期中考试数学成绩的频率分布直方图如所示，其中成绩分组区间是：[50，60]，[60，70]，[70，80]，[80，90]，[90，100]．
（1）a＝ ；
（2）样本数据落在[70，80）的频率为 ；
（3）根据频率分布直方图，估计这100名学生数学成绩的平均分为 ．
11．为贯彻落实中央、自治区和南宁市关于新冠肺炎疫情防控工作的决策部署，严格落实联防联控机制、严格执行报告制度，落实疫情管理．某高中学校，为此制定了很多防疫制度，新规章制度实施一段时间后，学校就新规章制度的执行、认知程度随机抽取100名学生进行问卷调查，调查卷共有20个问题，每个问题5分，调查结束后，发现这100名学生的成绩都在[75，100]内，按成绩分成5组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，绘制成如图所示的频率分布直方图，现在用分层抽样的方法在第3，4组共选取5人对新规章制度作深入学习，再从中选取2人深入的了解学习、执行的情况，则选取的2人来自于不同组的概率为 ．
12．从某校高一年级所有学生中随机选取100名学生，将他们参加知识竞赛的成绩的数据绘制成频率分布直方图，如图所示．从成绩在[70，80），[80，90]两组内的学生中，用分层抽样的方法选取了6人参加一项活动，若从这6人中随机选取两人担任正副队长，则这两人来自同一组的概率为
13．已知某地区中小学生人数如图所示，用分层抽样的方法抽取200名学生进行调查，则抽取的高中生人数为 ．
14．200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，则时速的众数、中位数的估计值分别为 ．
15．已知某地区中小学生的人数和近视率情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则抽取的高中生中近视的人数为 ．
16．某居民住宅小区图书室准备购买一定数量的书籍，为了满足不同年龄段居民的阅读需求，现随机抽取了40名阅读者进行调查，得到如图所示的频率分布直方图．则这40名阅读者的平均年龄为 ，中位数为 ．
（注：同一组中的数据用该组区间的中点值代表）
17．某学院为了调查学生2018年9月“健康使用手机”（健康使用手机指每天使用手机不超过3小时）的天数情况，随机抽取了80名学生作为样本，统计他们在30天内“健康使用手机”的天数，将所得数据分成以下六组：[0，5]，（5，10]，……，（25，30]，由此得到样本的频率分布直方图，如图所示，根据频率分布直方图，可计算出这80名学生中“健康使用手机”超过15天的人数为 ．
18．如图为某校1000名高一学生的体育测试成绩的频率分布直方图，如果要按照分层抽样方式抽取200名学生进行分析，则要抽取的[80，90）之间的学生人数是 ；估计这1000名学生的体育测试平均成绩为 ．
19．某小学为了解学生的身体素质情况，从1500名学生中随机抽取100名，测试他们一分钟跳绳的个数，统计数据得到样本的频率分布直方图如图．根据频率分布直方图估计，1500名学生中一分钟跳绳个数不少于80的学生数为 ．
20．已知某地区中小学学生人数和近视情况分别如图1和图2所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取20%的近视学生进行调查，则样本容量为 ，从中抽取的高中生近视人数为 ．
21．某高中为了解学生课外知识的积累情况，随机抽取200名同学参加课外知识测试，测试共5道题，每答对一题得20分，答错得0分．已知每名同学至少能答对2道题，得分不少于60分记为及格，不少于80分记为优秀，测试成绩百分比分布图如图所示，现有下列四个结论：
①该次课外知识测试及格率为92%；
②该次课外知识测试得满分的同学有30名；
③该次测试成绩的中位数大于测试成绩的平均数；
④若该校共有3000名学生，则课外知识测试成绩能得优秀的同学大约有1440名．
其中所有正确结论的序号是 ．
22．某调查机构调查了某地100个新生婴儿的体重，并根据所得数据画出了样本的频率分布直方图（如图所示），则新生婴儿的体重（单位：kg）在[3.6，4.4]的人数是 ．
23．为了解某市居民用水情况，通过抽样，获得了100位居民某年的月均用水量（单位：吨），将该数据按照[0，0.5），[0.5，1），…[4，4.5]分成9组，绘制了如图所示的频率分布直方图，政府要试行居民用水定额管理，制定了一个用水量标准a，使85%的居民用水量不超过a（假设a为整数），按平价收水费，超出a的部分按议价收费，则a的最小值为 ．
24．某校高三年级有400名学生，在一次数学测试中，成绩都在[80，130]（单位：分）内，其频率分布直方图如图，则这次测试数学成绩不低于100分的人数为
25．某妇产医院通过长期观察新生婴儿的体重，得到其频率分布直方图如图所示，则由此可以预测每1000名新生婴儿中，体重在[2700，3000）内的人数大约是 ．
26．某市高三数学抽样考试中，对90分以上（含90分）的成绩进行统计，其频率分布直方图如图所示，若130～140分数段的人数为90人，则90～100分数段的人数为 ．
三．解答题（共6小题）
27．由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》，某部门从参加创作的507名画师中随机抽出100名画师，得到画师年龄的频率分布表如下表所示．
（Ⅰ）求a，b的值；并补全频率分布直方图；
（Ⅱ）根据频率分布直方图估计这507名画师年龄的平均数；
（Ⅲ）在抽出的[20，25）岁的5名画师中有3名男画师，2名女画师．在这5名画师中任选两人去参加某绘画比赛，选出的恰好是一男一女的概率是多少？
28．某校为了解全校高中学生五一小长假参加实践活动的情况，抽查了100名学生，统计他们假期参加实践活动的时间，绘成的频率分布直方图如图所示．
（1）求这100名学生中参加实践活动时间在6～10小时内的人数；
（2）估计这100名学生参加实践活动时间的众数、中位数和平均数．
29．习近平同志在十九大报告中指出，要坚决打赢脱贫攻坚战，确保到2020年在我国现行标准下农村贫困人口实现脱贫，贫困是全部摘帽．某县在实施脱贫工作中因地制宜，着力发展枣树种核项目．该县种植的枣树在2020年获得大丰收，依据扶贫政策，所有红枣由经销商统一收购．为了更好的实现效益，县扶贫办从今年收获的红枣中随机选取100千克，进行质量检测，根据检测结果制成如图所示的频率分布直方图．如表是红枣的分级标准，其中一级品、二级品统称为优质品．
经销商与某农户签订了红枣收购协议，规定如下：从一箱红枣中任取4个进行检测，若4个均为优质品，则该箱红枣定为A类；若4个中仅有3个优质品，则再从该箱中任意取出1个，若这一个为优质品，则该箱红枣也定为A类；若4个中至多有一个优质品，则该箱红枣定为C类；其它情况均定为B类．已知每箱红枣重量为10千克，A类、B类、C类的红枣价格分别为每千克20元、16元、12元．现有两种装箱方案：
方案一：将红枣采用随机混装的方式装箱；
方案二：将红枣按一、二、三、四等级分别装箱，每箱的分拣成本为1元．
以频率代替概率解决下面的问题．
（1）如果该农户采用方案一装箱，求一箱红枣被定为A类的概率；
（2）根据所学知识判断，该农户采用哪种方案装箱更合适，并说明理由．
30．某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，并得到如图的频率分布直方图．
（1）若直方图中后四组的频数成等差数列，试估计全年级视力在5.0以下的人数；
（2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在1～50名和951～1000名的学生进行了调查，得到表中数据，根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系？
（3）在（2）中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好的护眼习惯，并且在这9人中任取3人，记名次在1～50的学生人数为X，求X的分布列和数学期望．
附：
K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)．
31．为了更好地刺激经济复苏，增加就业岗位，多地政府出台支持“地摊经济”的举措．某市城管委对所在城市约6000个流动商贩进行调查统计，发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等，各类商贩所占比例如图1．
（1）该市城管委为了更好地服务百姓，打算从流动商贩经营点中随机抽取100个进行政策问询．如果按照分层抽样的方式随机抽取，请问应抽取小吃类、果蔬类商贩各多少家？
（2）为了更好地了解商户的收入情况，工作人员还对某果蔬经营点最近40天的日收入进行了统计（单位：元），所得频率分布直方图如图2．
（ⅰ）请根据频率分布直方图估计该果蔬经营点的日平均收入（同一组中的数据用该组区间的中点值为代表）；
（ⅱ）若从该果蔬经营点的日收入超过200元的天数中随机抽取两天，求这两天的日收入至少有一天超过250元的概率．
32．已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下，抽出学生n人，成绩只有3、4、5三种分值，设x，y分别表示项目A与项目B成绩．例如：表中项目A成绩为5分的共7+9+4＝20人．已知x＝4且y＝5的概率是0.2．
（1）求n；
（2）若在该样本中，再按项目B的成绩分层抽样抽出20名学生，则y＝3的学生中应抽多少人？
（3）已知a≥9，b≥2，项目B为3分的学生中，求项目A得3分的人数比得4分人数多的概率．
人教版2022届一轮复习打地基练习 频率分布直方图
参考答案与试题解析
一．选择题（共8小题）
1．甲、乙、丙、丁四组人数分布如图所示，根据扇形统计图的情况可以知道丙、丁两组人数和为（ ）
A．150B．250C．300D．400
【分析】先根据甲组人数及其所占百分比可得总人数，再求出丙、丁两组人数占总人数的百分比，即可得解．
【解答】解：∵甲组人数为120人，占总人数的百分比为30%，
∴总人数为120÷30%＝400人，
∵丙、丁两组人数和占总人数的百分比为1﹣30%﹣7.5%＝62.5%
∴丙、丁两组人数和为400×62.5%＝250人．
故选：B．
2．某小区居民上网年龄分布图如图所示，现按照分层抽样的方法从该小区抽取一个容量为n的样本．若样本中90后比00后多52人，则n＝（ ）
A．400B．450C．500D．550
【分析】利用抽样比相等和比例的基本性质列式求解．
【解答】解：根据题意可知52n=21%−8%，解得n＝400．
故选：A．
3．近年来，我国继续大力发展公办幼儿园，积极扶持普惠性民办幼儿园，使得普惠性学前教育资源迅速增加．如图为国家统计局发布的2010～2019年幼儿园数量及学前教育毛入园率统计图．根据该统计图，下列说法不一定正确的是（ ）
注：毛入园率=适龄儿童入读幼儿园人数适龄儿童总人数．
A．2019年，全国共有幼儿园28.1万所
B．2019年的幼儿园数量比上一年大约增长了5.2%
C．2010～2019年我国适合入读幼儿园的人数在持续增加
D．2010～2019年我国幼儿园数量及学前教育毛入园率都在持续增加
【分析】适合入读幼儿园的人数不是该统计图表的研究对象，其变化规律不能在该图表中反映．
【解答】解：根据统计图表，A、D选项说法正确．
B选项，2019年幼儿园数量为28.1万所，2018年幼儿园数量为26.7万所，2019年增加28.1−26.726.7≈0.052，所以说法正确；
C选项，根据图表，学前教育毛入园率在增加，但是适合入读幼儿园的人数的变化不一定增加．
故选：C．
4．某班全体学生参加一次测试，将所得分数依次分组：[20，40），[40，60），[60，80），[80，100），绘制出如图所示的成绩频率分布直方图，若低于60分的人数是18，则该班的学生人数是（ ）
A．50B．54C．60D．64
【分析】根据频率分布直方图，求出得分低于60分的频率，再求该班的学生人数．
【解答】解：由频率分布直方图知，得分低于60分的频率为
（0.005+0.01）×20＝0.3，
∵低于60分的人数是18，
∴该班的学生人数是180.3=60
故选：C．
5．从某网络平台推荐的影视作品中抽取400部，统计其评分数据，将所得400个评分数据分为8组：[66，70），[70，74），…，[94，98），并整理得到如下的频率分布直方图，则评分在区间[82，86）内的影视作品数量是（ ）
A．20B．40C．64D．80
【分析】由频率分布直方图先求频率，再求频数，即评分在区间[82，86）内的影视作品数量即可．
【解答】解：由频率分布直方图知，
评分在区间[82，86）内的影视作品的频率为（86﹣82）×0.05＝0.2，
故评分在区间[82，86）内的影视作品数量是400×0.2＝80，
故选：D．
6．某校有200位教职员工，其每周用于锻炼所用时间的频率分布直方图如图所示．据图估计，每周锻炼时间在[10，12]小时内的人数为（ ）
A．18B．36C．54D．72
【分析】由频率分布直方图求出每周锻炼时间在[10，12]小时内的频率，由此能求出每周锻炼时间在[10，12]小时内的人数．
【解答】解：由频率分布直方图得：
每周锻炼时间在[10，12]小时内的频率为：1﹣（0.03+0.06+0.18+0.14）×2＝0.18，
∴每周锻炼时间在[10，12]小时内的人数为：200×0.18＝36．
故选：B．
7．已知某地区中小学生人数和近视情况分别如图（1）和图（2）所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则在抽取的高中生中，近视人数约为（ ）
A．1000B．40C．27D．20
【分析】根据分层抽样的定义建立比例关系即可得到结论．
【解答】解：由图1得样本容量为（3500+2000+4500）×2%＝10000×2%＝200，
抽取的高中生人数为2000×2%＝40人，
则近视人数为40×0.5＝20人，
故选：D．
8．某中学为了调查该校学生对于新冠肺炎防控的了解情况，组织了一次新冠肺炎防控知识竞赛，并从该学校1500名参赛学生中随机抽取了100名学生，并统计了这100名学生成绩情况（满分100分，其中80分及以上为优秀），得到了样本频率分布直方图（如图），根据频率分布直方图推测，这1500名学生中竞赛成绩为优秀的学生人数大约为（ ）
A．360B．420C．480D．540
【分析】由频率分布直方图求出样本中优秀的频率，由此根据频率分布直方图能推测这1500名学生中竞赛成绩为优秀的学生人数．
【解答】解：由频率分布直方图得：
样本中优秀的频率为（0.020+0.008）×10＝0.28，
∴根据频率分布直方图推测，这1500名学生中竞赛成绩为优秀的学生人数大约为：
1500×0.28＝420．
故选：B．
二．填空题（共18小题）
9．某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为[20，40），[40，60），[60，80），[80，100]．若低于60分的人数是6人，则参加该英语测试的学生人数是 20 ．
【分析】成绩低于60分有第一、二组数据，由频率分布直方图求出成绩低于60分的频率，再由低于60分的人数是6人，能求出参加该英语测试的学生人数．
【解答】解：∵成绩低于60分有第一、二组数据，
在频率分布直方图中，对应矩形的高分别为0.005，0.01，每组数据的组距为20，
则成绩低于60分的频率P＝（0.005+0.010）×20＝0.3，
∵低于60分的人数是6人，
∴参加该英语测试的学生人数是60.3=20．
故答案为：20．
10．某校100名学生期中考试数学成绩的频率分布直方图如所示，其中成绩分组区间是：[50，60]，[60，70]，[70，80]，[80，90]，[90，100]．
（1）a＝ 0.005 ；
（2）样本数据落在[70，80）的频率为 0.3 ；
（3）根据频率分布直方图，估计这100名学生数学成绩的平均分为 73 ．
【分析】（1）利用频率之和为1，列出关于a的方程，求解即可；
（2）利用频率分布直方图中小矩形的面积即为对应的概率，求解即可；
（3）利用频率分布直方图中平均数与中位数的计算方法进行分析求解，即可得到答案．
【解答】解：（1）由频率分布直方图可得，2a+0.04+0.03+0.02＝0.1，解得a＝0.005；
（2）样本数据落在[70，80）的频率为0.03×10＝0.3；
（3）根据频率分布直方图，平均数为55×0.05+65×0.4+75×0.3+85×0.2+95×0.05＝73．
11．为贯彻落实中央、自治区和南宁市关于新冠肺炎疫情防控工作的决策部署，严格落实联防联控机制、严格执行报告制度，落实疫情管理．某高中学校，为此制定了很多防疫制度，新规章制度实施一段时间后，学校就新规章制度的执行、认知程度随机抽取100名学生进行问卷调查，调查卷共有20个问题，每个问题5分，调查结束后，发现这100名学生的成绩都在[75，100]内，按成绩分成5组：第1组[75，80），第2组[80，85），第3组[85，90），第4组[90，95），第5组[95，100]，绘制成如图所示的频率分布直方图，现在用分层抽样的方法在第3，4组共选取5人对新规章制度作深入学习，再从中选取2人深入的了解学习、执行的情况，则选取的2人来自于不同组的概率为 35 ．
【分析】根据频率分布直方图，利用频率、频数与样本容量的关系即可解答．
【解答】解：由题可知第3组的人数为0.06×5×100＝30；第4组的人数为0.04×5×100＝20．
现在用分层抽样的方法在第3，4组共50人中选取5人对新规章制度作深入学习，即抽取比例为550=110，
则采用分层抽样在两组中选取的人数分别为3，2，
则选取的2人来自于不同组的概率为C31⋅C21C52=35，
故答案为：35．
12．从某校高一年级所有学生中随机选取100名学生，将他们参加知识竞赛的成绩的数据绘制成频率分布直方图，如图所示．从成绩在[70，80），[80，90]两组内的学生中，用分层抽样的方法选取了6人参加一项活动，若从这6人中随机选取两人担任正副队长，则这两人来自同一组的概率为 715
【分析】从成绩在[70，80）的学生中抽取4人，从成绩在[80，90）的学生中抽取2人，从这6人中随机选取两人担任正副队长，基本事件总数n=C62=15，这两人来自同一组包含的基本事件个数m=C42+C22=7，由此能求出这两人来自同一组的概率．
【解答】解：从成绩在[70，80），[80，90]两组内的学生中，用分层抽样的方法选取了6人参加一项活动，
则从成绩在[70，80）的学生中抽取：6×+0.010=4人，
从成绩在[80，90）的学生中抽取：6×+0.010=2人，
从这6人中随机选取两人担任正副队长，
基本事件总数n=C62=15，
这两人来自同一组包含的基本事件个数m=C42+C22=7，
∴这两人来自同一组的概率为p=mn=715．
故答案为：715．
13．已知某地区中小学生人数如图所示，用分层抽样的方法抽取200名学生进行调查，则抽取的高中生人数为 50 ．
【分析】由分层抽样的方法和扇形统计图，能求出抽取的高中生人数．
【解答】解：用分层抽样的方法抽取200名学生进行调查，
由扇形统计图得：
抽取的高中生人数为：
200×30004500+4500+3000=50．
故答案为：50．
14．200辆汽车通过某一段公路时的时速的频率分布直方图如图所示，则时速的众数、中位数的估计值分别为 65，62.5 ．
【分析】由频率分布直方图能估计时速的众数和中位数．
【解答】解：由频率分布直方图得：
时速的众数为：60+702=65，
[40，60）的频率为：（0.01+0.03）×10＝0.4，
[60，70）的频率为：0.04×10＝0.4，
∴时速的中位数为：60+0.5−0.40.4×10=62.5．
故答案为：65，62.5．
15．已知某地区中小学生的人数和近视率情况分别如图1和图2所示，为了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则抽取的高中生中近视的人数为 20 ．
【分析】先计算出高中生人数，再根据近视率求得结果．
【解答】解：用分层抽样的方法抽取2%的学生进行调查，抽取的高中生人数为10000×2%×420=40人，
则抽取的高中生中近视的人数为40×50%＝20人．
故答案为：20．
16．某居民住宅小区图书室准备购买一定数量的书籍，为了满足不同年龄段居民的阅读需求，现随机抽取了40名阅读者进行调查，得到如图所示的频率分布直方图．则这40名阅读者的平均年龄为 54 ，中位数为 55 ．
（注：同一组中的数据用该组区间的中点值代表）
【分析】由频率分布直方图的性质能求出这40名阅读者的平均年龄和中位数．
【解答】解：由频率分布直方图得：
这40名阅读者的平均年龄为：
25×0.005×10+35×0.010×10+45×0.020×10+55×0.030×10+65×0.025×10+75×0.010×10＝54．
[20，50）的频率为：（0.005+0.010+0.020）×10＝0.35，
[50，60）的频率为：0.030×10＝0.3，
∴中位数为：
50+0.5−0.350.3×10=55．
故答案为：54，55．
17．某学院为了调查学生2018年9月“健康使用手机”（健康使用手机指每天使用手机不超过3小时）的天数情况，随机抽取了80名学生作为样本，统计他们在30天内“健康使用手机”的天数，将所得数据分成以下六组：[0，5]，（5，10]，……，（25，30]，由此得到样本的频率分布直方图，如图所示，根据频率分布直方图，可计算出这80名学生中“健康使用手机”超过15天的人数为 54 ．
【分析】由频率分布直方图求出健康使用手机超过15天的频率，由此能求出这80名学生中“健康使用手机”超过15天的人数．
【解答】解：由频率分布直方图知，健康使用手机超过15天的频率为：
（0.07+0.05+0.015）×5＝0.675，
∴这80名学生中“健康使用手机”超过15天的人数为：
0.675×80＝54．
故答案为：54．
18．如图为某校1000名高一学生的体育测试成绩的频率分布直方图，如果要按照分层抽样方式抽取200名学生进行分析，则要抽取的[80，90）之间的学生人数是 40 ；估计这1000名学生的体育测试平均成绩为 73 ．
【分析】根据已知条件，结合频率与频数的关系，以及平均数公式，即可求解．
【解答】解：∵抽取的[80，90）之间的频率为10×0.02＝0.2，
∴抽取的[80，90）之间的学生人数是200×0.2＝40，
估计这1000名学生的体育测试平均成绩为55×0.005×10+65×0.04×10+75×0.02×10+95×0.005×10＝73．
故答案为：40，73．
19．某小学为了解学生的身体素质情况，从1500名学生中随机抽取100名，测试他们一分钟跳绳的个数，统计数据得到样本的频率分布直方图如图．根据频率分布直方图估计，1500名学生中一分钟跳绳个数不少于80的学生数为 420 ．
【分析】由频率分布直方图求出一分钟跳绳个数不少于80的频率，由此能求出1500名学生中一分钟跳绳个数不少于80的学生数．
【解答】解：由频率分布直方图得：
一分钟跳绳个数不少于80的频率为：（0.020+0.008）×10＝0.28，
∴1500名学生中一分钟跳绳个数不少于80的学生数为：
1500×0.28＝420．
故答案为：420．
20．已知某地区中小学学生人数和近视情况分别如图1和图2所示，为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取20%的近视学生进行调查，则样本容量为 4000 ，从中抽取的高中生近视人数为 400 ．
【分析】用分层抽样的方法抽取20%的近视学生进行调查，利用分层抽样、频数分布表、条形图的性质求出样本容量和从中抽取的高中生近视人数．
【解答】解：由题意得：
用分层抽样的方法抽取20%的近视学生进行调查，
则样本容量为：（9000+7000+4000）×20%＝4000．
从中抽取的高中生近视人数为：
4000×20%×50%＝400．
故答案为：4000，400．
21．某高中为了解学生课外知识的积累情况，随机抽取200名同学参加课外知识测试，测试共5道题，每答对一题得20分，答错得0分．已知每名同学至少能答对2道题，得分不少于60分记为及格，不少于80分记为优秀，测试成绩百分比分布图如图所示，现有下列四个结论：
①该次课外知识测试及格率为92%；
②该次课外知识测试得满分的同学有30名；
③该次测试成绩的中位数大于测试成绩的平均数；
④若该校共有3000名学生，则课外知识测试成绩能得优秀的同学大约有1440名．
其中所有正确结论的序号是 ①③ ．
【分析】利用测试成绩百分比分布图直接求解．
【解答】解：由图可知及格率＝1﹣8%＝92%，故①正确；
该次课外知识测试满分同学的百分比＝1﹣8%﹣32%﹣48%＝12%，12%×200＝24名，故②错误；
中位数为80分，平均数＝40×8%+60×32%+80×48%+100×12%＝72.8分，故③正确；
3000×（48%+12%）＝1800，故④错误．
故答案为：①③．
22．某调查机构调查了某地100个新生婴儿的体重，并根据所得数据画出了样本的频率分布直方图（如图所示），则新生婴儿的体重（单位：kg）在[3.6，4.4]的人数是 20 ．
【分析】求出[3.6，4.4]的概率，再求出即可．
【解答】解：根据图象，新生婴儿的体重（单位：kg）在[3.6，4.4]的概率为0.4（0.375+0.125）＝0.2，
由100×0.2＝20，
故答案为：20．
23．为了解某市居民用水情况，通过抽样，获得了100位居民某年的月均用水量（单位：吨），将该数据按照[0，0.5），[0.5，1），…[4，4.5]分成9组，绘制了如图所示的频率分布直方图，政府要试行居民用水定额管理，制定了一个用水量标准a，使85%的居民用水量不超过a（假设a为整数），按平价收水费，超出a的部分按议价收费，则a的最小值为 3吨 ．
【分析】求出[0，0.5）的频数为4，[0.5，1）的频数为8，[1.5，2）的频数为22，[2，2.5）的频数为25，[2.5，3）的频数为4，[3，3.5）的频数为4，[4，4.5）的频数为2，4+8+15+22+15+14＝86，由此能求出a的最小值．
【解答】解：[0，0.5）的频数为0.08×0.5×100＝4，
[0.5，1）的频数为0.16×0.5×100＝8，
[1.5，2）的频数为0.44×0.5×100＝22，
[2，2.5）的频数为0.5×0.5×100＝25，
[2.5，3）的频数为0.28×0.5×100＝4．
[3，3.5）的频数为0.08×0.5×100＝4，
[4，4.5）的频数为0.04×0.5×100＝2，
4+8+15+22+15+14＝86，
∴前6组占86%，a为3吨．
故答案为：3吨．
24．某校高三年级有400名学生，在一次数学测试中，成绩都在[80，130]（单位：分）内，其频率分布直方图如图，则这次测试数学成绩不低于100分的人数为 220
【分析】由频率分布直方图得（2a+0.040+0.030+0.020）×10＝1，求出a＝0.005，由此能求出这次测试数学成绩不低于100分的频率．
【解答】解：由频率分布直方图得：
（2a+0.040+0.030+0.020）×10＝1，
解得a＝0.005，
∴这次测试数学成绩不低于100分的频率为：
1﹣（0.005+0.040）×10＝0.55
∴这次测试数学成绩不低于100分的人数为：400×0.55＝220．
故答案为：220．
25．某妇产医院通过长期观察新生婴儿的体重，得到其频率分布直方图如图所示，则由此可以预测每1000名新生婴儿中，体重在[2700，3000）内的人数大约是 300 ．
【分析】由频率分布直方图计算体重在[2700，3000）内的人数频率，然后乘以1000可得所求．
【解答】解：体重在[2700，3000）内的人数大约是0.001×300×1000＝300．
故答案为：300．
26．某市高三数学抽样考试中，对90分以上（含90分）的成绩进行统计，其频率分布直方图如图所示，若130～140分数段的人数为90人，则90～100分数段的人数为 720 ．
【分析】由频率分布直方图得90～100分数段的频率为0.4，130～140分数段的人数为90人，130～140分数段频率为0.05，由此能求出90～100分数段的人数．
【解答】解：由频率分布直方图得90～100分数段的频率为0.4，
130～140分数段的人数为90人，130～140分数段频率为0.05，
∴90～100分数段的人数为：90×．
故答案为：720．
三．解答题（共6小题）
27．由507名画师集体创作的999幅油画组合而成了世界名画《蒙娜丽莎》，某部门从参加创作的507名画师中随机抽出100名画师，得到画师年龄的频率分布表如下表所示．
（Ⅰ）求a，b的值；并补全频率分布直方图；
（Ⅱ）根据频率分布直方图估计这507名画师年龄的平均数；
（Ⅲ）在抽出的[20，25）岁的5名画师中有3名男画师，2名女画师．在这5名画师中任选两人去参加某绘画比赛，选出的恰好是一男一女的概率是多少？
【分析】（Ⅰ）由频率分布表能求出a，b，能补全频率分布直方图．
（Ⅱ）利用频率分布直方图能求出507名画师中年龄的平均数的估计值．
（Ⅲ）三名男画师记为a，b，c，两名女画师记为1，2，利用列举法能求出选出的恰好是一男一女的概率．
【解答】（本小题满分12分）
解：（Ⅰ）由频率分布表得：a＝100×0.200＝20，
b=35100=0.35，
∴补全频率分布直方图如图所示：
（Ⅱ）507名画师中年龄的平均数的估计值为：
22.5×0.05+27.5×0.2+32.5×0.35+37.5×0.3+42.5×0.1＝33.5（岁）．
（Ⅲ）三名男画师记为a，b，c，两名女画师记为1，2，
五人中任选两人的所有基本事件如下：
（a，b），（a，c），（a，1），（a，2），（b，c），（b，1），（b，2），（c，1），（c，2），（1，2），共10个基本事件，
其中一男一女的是（a，1），（a，2），（b，1），（b，2），（c，1），（c，2），共6个基本事件，
∴选出的恰好是一男一女的概率p=610=35．
28．某校为了解全校高中学生五一小长假参加实践活动的情况，抽查了100名学生，统计他们假期参加实践活动的时间，绘成的频率分布直方图如图所示．
（1）求这100名学生中参加实践活动时间在6～10小时内的人数；
（2）估计这100名学生参加实践活动时间的众数、中位数和平均数．
【分析】（1）利用频率分布直方图能求出100名学生中参加实践活动的时间在6～10小时内的人数．
（2）由频率分布直方图可以看出最高矩形横轴上的中点为7，由此能求出这100名学生参加实践活动时间的众数的估计值；由（0.04+0.12+0.15+a+0.05）×2＝1，求出a＝0.14，由此利用频率分布直方图能求出这100名学生参加实践活动时间的中位数和平均数．
【解答】解：（1）依题意，100名学生中参加实践活动的时间在6～10小时内的人数为：
100×[1﹣（0.04+0.12+0.05）×2]＝58，
即这100名学生中参加实践活动时间在6～10小时内的人数为58．
（2）由频率分布直方图可以看出最高矩形横轴上的中点为7，
故这100名学生参加实践活动时间的众数的估计值为7小时，
由（0.04+0.12+0.15+a+0.05）×2＝1，解得a＝0.14，
则6+0.5−(0.04+0.12)×20.15=7.2，
即这100名学生参加实践活动时间的中位数为7.2小时，
这100名学生参加实践活动时间的平均数为：
0.04×2×3+0.12×2×5+0.15×2×7+0.14×2×9+0.05×2×11＝7.16小时．
29．习近平同志在十九大报告中指出，要坚决打赢脱贫攻坚战，确保到2020年在我国现行标准下农村贫困人口实现脱贫，贫困是全部摘帽．某县在实施脱贫工作中因地制宜，着力发展枣树种核项目．该县种植的枣树在2020年获得大丰收，依据扶贫政策，所有红枣由经销商统一收购．为了更好的实现效益，县扶贫办从今年收获的红枣中随机选取100千克，进行质量检测，根据检测结果制成如图所示的频率分布直方图．如表是红枣的分级标准，其中一级品、二级品统称为优质品．
经销商与某农户签订了红枣收购协议，规定如下：从一箱红枣中任取4个进行检测，若4个均为优质品，则该箱红枣定为A类；若4个中仅有3个优质品，则再从该箱中任意取出1个，若这一个为优质品，则该箱红枣也定为A类；若4个中至多有一个优质品，则该箱红枣定为C类；其它情况均定为B类．已知每箱红枣重量为10千克，A类、B类、C类的红枣价格分别为每千克20元、16元、12元．现有两种装箱方案：
方案一：将红枣采用随机混装的方式装箱；
方案二：将红枣按一、二、三、四等级分别装箱，每箱的分拣成本为1元．
以频率代替概率解决下面的问题．
（1）如果该农户采用方案一装箱，求一箱红枣被定为A类的概率；
（2）根据所学知识判断，该农户采用哪种方案装箱更合适，并说明理由．
【分析】（1）计算从红枣中任意取出一个为优质品的概率值，求出采用方案一装箱时一箱红枣被定为A类的概率值；
（2）计算该农户采用方案一装箱，每箱红枣收入的数学期望和采用方案二装箱，每箱红枣收入的数学期望值，比较即可．
【解答】解：（1）从红枣中任意取出一个，则该红枣为优质品的概率是12，
记“如果该农户采用方案一装箱，一箱红枣被定为A类”为事件A，
则P(A)=(12)4+C41(12)3(1−12)×12=316；
（2）记“如果该农户采用方案一装箱，一箱红枣被定为B类”为事件B，
“如果该农户采用方案一装箱，一箱红枣被定为C类”为事件C，
则P(C)=(1−12)4+C43×12⋅(1−12)3=516，
P(B)=1−P(A)−P(C)=12，
所以如果该农户采用方案一装箱，每箱红枣收入的数学期望为：
200×316+160×12+120×516=155（元）；
由题意可知，如果该农户采用方案二装箱，
则一箱红枣被定为A类的概率为12，被定为C类的概率也为12，
所以如果该农户采用方案二装箱，每箱红枣收入的数学期望为：
200×12+120×12−1=159（元）；
所以该农户采用方案二装箱更合适．
30．某学校研究性学习小组对该校高三学生视力情况进行调查，在高三的全体1000名学生中随机抽取了100名学生的体检表，并得到如图的频率分布直方图．
（1）若直方图中后四组的频数成等差数列，试估计全年级视力在5.0以下的人数；
（2）学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在1～50名和951～1000名的学生进行了调查，得到表中数据，根据表中的数据，能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系？
（3）在（2）中调查的100名学生中，按照分层抽样在不近视的学生中抽取了9人，进一步调查他们良好的护眼习惯，并且在这9人中任取3人，记名次在1～50的学生人数为X，求X的分布列和数学期望．
附：
K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)．
【分析】（1）由频率分布直方图求出对应的频数和频率；
（2）由列联表中数据计算K2，对照临界值得出结论；
（3）由题意知随机变量X的可能取值，计算对应的概率值，
写出X的分布列，求出数学期望值．
【解答】解：（1）设各组的频率为fi（i＝1，2，3，4，5，6），
由图可知，第一组有3人，第二组7人，第三组27人，
因为后四组的频数成等差数列，所以后四组频数依次为27，24，21，18；
所以视力在5.0以下的频数为3+7+27+24+21＝82人，
故全年级视力在5.0以下的人数约为1000×82100=820人；
（2）由列联表中数据，计算K2=100×(41×18−32×9)250×50×73×27=30073≈4.110＞3.841，
因此在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系；
（3）依题意9人中年级名次在1～50名和951～1000名分别有3人和6人，
则X可取值为0、1、2、3；
且P（X＝0）=C63C93=2084，P（X＝1）=C62⋅C31C93=4584，
P（X＝2）=C61⋅C32C93=1884，P（X＝3）=C33C93=184；
所以X的分布列为
X的数学期望为E（X）＝0×2084+1×4584+2×1884+3×184=1．
31．为了更好地刺激经济复苏，增加就业岗位，多地政府出台支持“地摊经济”的举措．某市城管委对所在城市约6000个流动商贩进行调查统计，发现所售商品多为小吃、衣帽、果蔬、玩具、饰品等，各类商贩所占比例如图1．
（1）该市城管委为了更好地服务百姓，打算从流动商贩经营点中随机抽取100个进行政策问询．如果按照分层抽样的方式随机抽取，请问应抽取小吃类、果蔬类商贩各多少家？
（2）为了更好地了解商户的收入情况，工作人员还对某果蔬经营点最近40天的日收入进行了统计（单位：元），所得频率分布直方图如图2．
（ⅰ）请根据频率分布直方图估计该果蔬经营点的日平均收入（同一组中的数据用该组区间的中点值为代表）；
（ⅱ）若从该果蔬经营点的日收入超过200元的天数中随机抽取两天，求这两天的日收入至少有一天超过250元的概率．
【分析】（1）由扇形统计图求出小吃类所占比例为40%，由此按照分层抽样的方式随机抽取，能求出应抽取小吃类、果蔬类商贩各多少家．
（2）（i）由频率分布直方图能求出该果蔬经营点的日平均收入．
（ⅱ）该果蔬经营点的日收入超过200元的天数为6，其中超过250元的有2天，记日收入超过250元的2天为a1，a2，其余4天为b1，b2，b3，b4，随机抽取两天，利用列举法能求出这两天的日收入至少有一天超过250元的概率．
【解答】解：（1）由题意知，小吃类所占比例为：
1﹣25%﹣15%﹣10%﹣5%﹣5%＝40%，
按照分层抽样的方式随机抽取，
应抽取小吃类商贩：100×40%＝40（家），
果蔬类商贩100×15%＝15（家）．
（2）（i）该果蔬经营点的日平均收入为：
（75×0.002+125×0.009+175×0.006+225×0.002+275×0.001）×50＝152.5（元）．
（ⅱ）该果蔬经营点的日收入超过200元的天数为6，其中超过250元的有2天，
记日收入超过250元的2天为a1，a2，其余4天为b1，b2，b3，b4，
随机抽取两天的所有可能情况为：
（a1，a2），（a1，b1），（a1，b2），（a1，b3），（a1，b4），（a2，b1），（a2，b2），（a2，b3），
（a2，b4），（b1，b2），（b1，b3），（b1，b4），（b2，b3），（b2，b4），（b3，b1），共15种，
其中至少有一天超过250元的所有可能情况为：
（a1，a2），（a1，b1），（a1，b2），（a1，b3），（a1，b4），（a2，b1），（a2，b2），（a2，b3），（a2，b4），共9种．
所以这两天的日收入至少有一天超过250元的概率为P=915=35．
32．已知某职业技能培训班学生的项目A与项目B成绩抽样统计表如下，抽出学生n人，成绩只有3、4、5三种分值，设x，y分别表示项目A与项目B成绩．例如：表中项目A成绩为5分的共7+9+4＝20人．已知x＝4且y＝5的概率是0.2．
（1）求n；
（2）若在该样本中，再按项目B的成绩分层抽样抽出20名学生，则y＝3的学生中应抽多少人？
（3）已知a≥9，b≥2，项目B为3分的学生中，求项目A得3分的人数比得4分人数多的概率．
【分析】（1）利用频率、频数的关系：频率=频数数据总和即可求得n；
（2）由题意y＝3的学生总人数为100﹣（7+20+5+9+18+6），据20100=m35即可求得y＝3的学生中应抽多少人；
（3）由题意可知，满足条件的（a，b）的人数，再计算出b＞a的人数，最后算出它们的比值即可．
【解答】解：（1）由题意可知20n=0.2，
得n＝100人；（3分）
（2）由题意y＝3的学生总人数为100﹣（7+20+5+9+18+6）＝35，
设应在y＝3的学生抽m人，则20100=m35，m＝7人（7分）
（3）由题意可知a+b＝35﹣4＝31人，且a≥9，b≥2，
满足条件的（a，b）有（9，22），（10，21），（29，2），
共有21组，其中b＞a的有7组． （9分）
记C表示时间“项目A得（3分）的人数比得（4分）人数多”
则P（C）=721=13． （11分）
答：（1）n＝100人，（2）则y＝3的学生中应抽7人． （12分）小学
初中
高中
人数
9000
7000
4000
分组（岁）
频数
频率
[20，25）
5
0.050
[25，30）
a
0.200
[30，35）
35
b
[35，40）
30
0.300
[40，45）
10
0.100
合计
100
1.00
等级
四级品
三级品
二级品
一级品
红枣纵径/mm
[30，35）
[35，40）
[40，45）
[45，50]
年级名次
是否近视
1～50
951～1000
近视
41
32
不近视
9
18
P（K2≥k）
0.10
0.05
0.025
0.010
0.005
k
2.706
3.841
5.024
6.635
7.879
小学
初中
高中
人数
9000
7000
4000
分组（岁）
频数
频率
[20，25）
5
0.050
[25，30）
a
0.200
[30，35）
35
b
[35，40）
30
0.300
[40，45）
10
0.100
合计
100
1.00
等级
四级品
三级品
二级品
一级品
红枣纵径/mm
[30，35）
[35，40）
[40，45）
[45，50]
年级名次
是否近视
1～50
951～1000
近视
41
32
不近视
9
18
P（K2≥k）
0.10
0.05
0.025
0.010
0.005
k
2.706
3.841
5.024
6.635
7.879
X
0
1
2
3
P
2084
4584
1884
184