人教版2022届一轮复习打地基练习 茎叶图

这是一份人教版2022届一轮复习打地基练习 茎叶图，共35页。
人教版2022届一轮复习打地基练习 茎叶图
一．选择题（共16小题）
1．国庆70周年庆典磅礴而又欢快的场景，仍历历在目．已知庆典中某省的游行花车需要用到某类花卉，而该类花卉有甲、乙两个品种，花车的设计团队对这两个品种进行了检测．现从两个品种中各抽测了10株的高度，得到如下茎叶图．下列描述正确的是（　　）

A．甲品种的平均高度大于乙品种的平均高度，且甲品种比乙品种长的整齐
B．甲品种的平均高度大于乙品种的平均高度，但乙品种比甲品种长的整齐
C．乙品种的平均高度大于甲品种的平均高度，且乙品种比甲品种长的整齐
D．乙品种的平均高度大于甲品种的平均高度，但甲品种比乙品种长的整齐
2．某同学进入高三后，4次月考的数学成绩的茎叶图如图，则该同学数学成绩的方差是（　　）

A．125 B．45 C．5 D．35
3．如图是2013年中央电视台举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（　　）

A．85，1.6 B．84，4 C．84，1.6 D．85，4
4．如图是某运动员在某个赛季得分的茎叶图统计表，则该运动员得分的中位数是（　　）

A．2 B．24 C．23 D．26
5．某超市抽取13袋袋装食用盐，对其质量（单位：g）进行统计，得到如图茎叶图，若从这13袋食用盐中随机选取1袋，则该袋食用盐的质量在[499，501]内的概率为（　　）

A．513 B．613 C．713 D．813
6．某学校A、B两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下，

①A班数学兴趣小组的平均成绩高于B班的平均成绩；
②A班数学兴趣小组成绩的众数小于B班成绩的众数；
③A班数学兴趣小组成绩的极差小于B班成绩的极差；
④A班数学兴趣小组成绩的中位数大于B班成绩的中位数．
其中正确结论的编号为（　　）
A．①④ B．②③ C．②④ D．①③
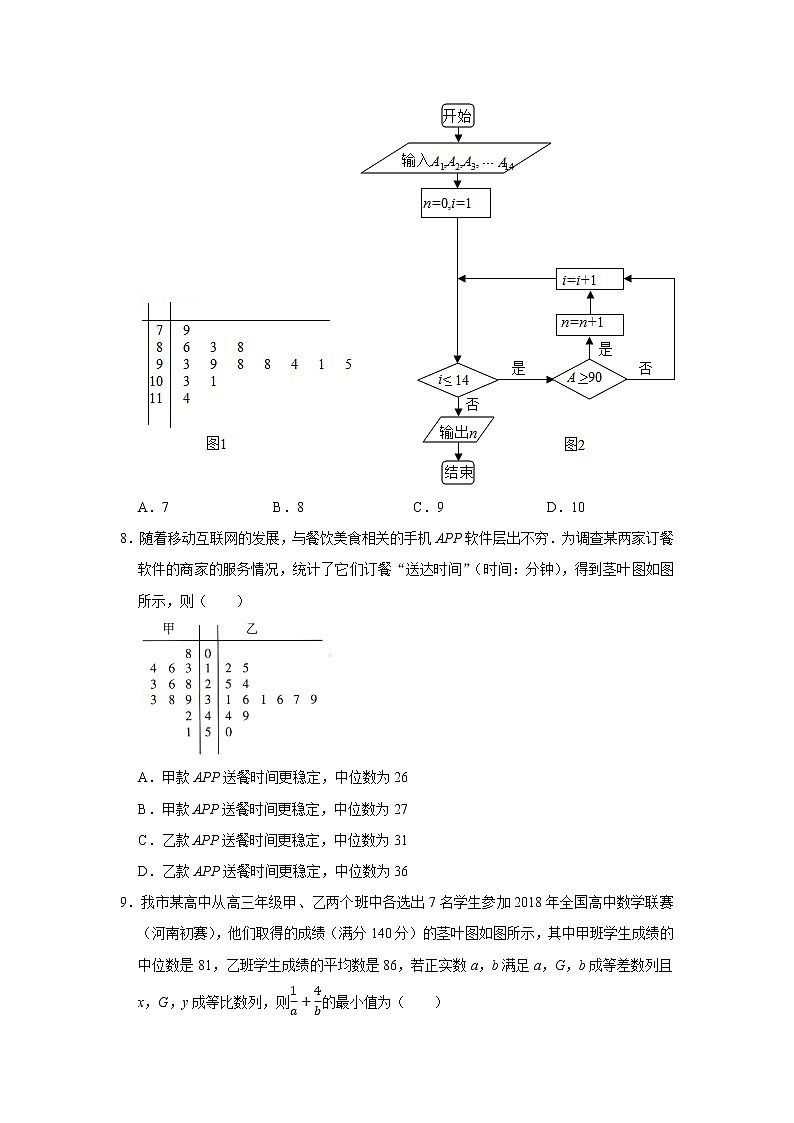
7．图1是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到14次的考试成绩依次记为A1，A2，…，A14．图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是（　　）

A．7 B．8 C．9 D．10
8．随着移动互联网的发展，与餐饮美食相关的手机APP软件层出不穷．为调查某两家订餐软件的商家的服务情况，统计了它们订餐“送达时间”（时间：分钟），得到茎叶图如图所示，则（　　）

A．甲款APP送餐时间更稳定，中位数为26
B．甲款APP送餐时间更稳定，中位数为27
C．乙款APP送餐时间更稳定，中位数为31
D．乙款APP送餐时间更稳定，中位数为36
9．我市某高中从高三年级甲、乙两个班中各选出7名学生参加2018年全国高中数学联赛（河南初赛），他们取得的成绩（满分140分）的茎叶图如图所示，其中甲班学生成绩的中位数是81，乙班学生成绩的平均数是86，若正实数a，b满足a，G，b成等差数列且x，G，y成等比数列，则1a+4b的最小值为（　　）

A．49 B．2 C．94 D．9
10．已知七位评委为某民族舞蹈参赛演员评定分数的茎叶图如图中左边为十位数，右边为个位数．去掉一个最高分和一个最低分，所剩数据的平均数和方差分别为（　　）

A．84，4.84 B．84，1.6 C．85，1.6 D．85，4
11．近几年，我国农村电子商务发展迅速，使得农副产品能够有效地减少流通环节，降低流通成本，直接提高了农民的收益．某农村电商对一个月内每天的顾客人数进行了统计，得到样本的茎叶图（如图所示），则该样本的中位数、众数、极差分别是（　　）

A．46.5，48，60 B．47，48，60 C．46.5，48，55 D．46.5，51，60
12．如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩（单位：分）．则甲组数据的中位数，乙组数据的平均数分别为（　　）

A．12，15 B．15，15 C．15，15.9 D．15，16.8
13．甲、乙两名篮球运动员最近五场比赛的得分如茎叶图所示，则（　　）

A．甲的中位数和平均数都比乙高
B．甲的中位数和平均数都比乙低
C．甲的中位数比乙的中位数高，但平均数比乙的平均数低
D．甲的中位数比乙的中位数低，但平均数比乙的平均数高
14．如图是某次比赛上七位评委为某选手打出的分数的茎叶图，若去掉一个最高分和最低分，则所剩数据的平均数为（　　）

A．84 B．85 C．86 D．87
15．某社区安置了15个体温检测点，每个检测点每天检测的人数都是随机的，不受位置等因素影响，如图是由某天检测人数绘制的茎叶图，则某个检测点某天检测人数达145及以上的概率是（　　）

A．715 B．815 C．13 D．23
16．如图是8位学生的某次数学测试成绩的茎叶图，则下列说法正确的是（　　）

A．众数为7 B．极差为18
C．中位数是64.5 D．平均数是64
二．多选题（共1小题）
17．某校举行学习党史知识比赛，甲、乙两个班各有10名同学参加，根据成绩绘制茎叶图如下，则（　　）

A．x甲＞x乙 B．x甲＜x乙 C．S2甲＜S2乙 D．S2甲＞S2乙
三．填空题（共17小题）
18．为调动我市学生参与课外阅读的积极性，我市制定了《进一步加强中小学课外阅读指导的实施方案》，有序组织学生开展课外阅读活动．某校语文老师在班里开展了一次诗词默写比赛，班里40名学生得分数据的茎叶图如图．若规定得分不低于85分的学生得到“诗词达人的”称号，低于85分且不低于70分的学生得到“诗词能手”的称号，其他学生得到“诗词爱好者”的称号．根据该次比赛的成绩，按照称号的不同，进行分层抽样抽选15名学生，则抽选的学生中获得“诗词能手”称号的人数为　 　．

19．如图所示的茎叶图记录了甲乙两位射箭运动员的5次比赛成绩（单位：环），若两位运动员平均成绩相同，则成绩较为稳定（方差较小）的那位运动员成绩的方差为　 　．

20．甲、乙两名学生的六次数学测验成绩（百分制）的茎叶图如图所示．
①甲同学成绩的中位数小于乙同学成绩的中位数；
②甲同学的平均分比乙同学的平均分高；
③甲同学的平均分比乙同学的平均分低；
④甲同学成绩的方差小于乙同学成绩的方差．
上面说法正确的是 　 　．

21．某学校开展了“国学”系列讲座活动，为了了解活动效果，用分层抽样的方法从高一年级所有学生中抽取10人进行国学素养测试，这10名同学的性别和测试成绩（百分制）的茎叶图如图所示．则男生成绩的75%分位数为　 　；已知高一年级中男生总数为80人，试估计高一年级学生总数为　 　．

22．随机抽取某班10名同学，测量他们的身高（单位：cm）获得身高数据的茎叶图（如图），则这个班的众数为　 　，极差　 　．

23．如图茎叶图记录了甲、乙两组各5名工人某日的产量数据（单位：件），若这两组数据的中位数和平均数都相等，则x+y的值为　 　．

24．如图所示的茎叶图记录了甲、乙两位学生5次体育测试的成绩，若这两组数据的平均值等，极差也相等，则学生乙体育测试的最高成绩为　 　．

25．从某工厂生产线上随机抽取16件零件，测量其内径数据从小到大依次排列如下（单位：mm）：1.12，1.15，1.21，1.23，1.25，1.25，1.26，1.30，1.30，1.32，1.34，1.35，1.37，1.38，1.41，1.42．据此可估计该生产线上大约有25%的零件内径小于等于　 　mm，大约有30%的零件内径大于　 　mm．
26．从甲、乙两个班中各随机选出15名同学进行随堂测验，成绩的茎叶图如图所示，则甲、乙两班的最高成绩分别是　 　，　 　.从图中看，　 　班的平均成绩较高．

27．一次体操比赛中，7位裁判为某运动员打出的分数如茎叶图所示（其中茎表示十位数，叶表示个位数），去掉一个最高分和一个最低分后，剩余数据的平均数为　 　．

28．甲、乙两位同学高三8次物理模拟考试成绩如图所示，甲同学的平均成绩与乙同学的众数相等，则m＝　 　．

29．在某社区举行的“讲文明，树新风”答题竞赛中，根据甲、乙两组选手的成绩，绘制的茎叶图如图所示，
甲组成绩的25%分位数为　 　；设甲、乙两组成的方差分别为s甲2，s乙2，那么s甲2　 　s乙2．（填“＞”或“＜”或“＝”）

30．甲、乙两位同学的5次考试成绩如茎叶图所示，则成绩较稳定的那位学生成绩的方差为　 　．

31．甲、乙两名篮球运动员在几场比赛中得分的茎叶图如图所示，则甲、乙两人在这几场比赛中得分的中位数之和为 　 　．

32．某次数学测验五位同学的成绩分布茎叶图如图，则这五位同学数学成绩的方差为　 　．

33．在某项技能测试中，甲乙两人的成绩（单位：分）记录在如图所示的茎叶图中，其中甲的某次成绩不清晰，用字母a代替．已知甲乙成绩的中位数相等，那么a的值为　 　．

34．在某项技能测试中，甲乙两人的成绩（单位：分）记录在如图所示的茎叶图中，其中甲的某次成绩不清晰，用字母a代替．已知甲乙成绩的平均数相等，那么甲成绩的中位数为　 　．

四．解答题（共5小题）
35．某电视台举办青年歌手大奖赛，有10名评委打分，已知甲、乙两名选手演唱后的打分情况如茎叶图所示：

（Ⅰ）从统计的角度，你认为甲与乙比较，演唱水平怎样？
（Ⅱ）现场有3名点评嘉宾A、B、C，每位选手可以从中选2位进行指导，若选手选每位点评嘉宾的可能性相等，求甲乙两选手选择的点评嘉宾恰重复一人的概率．
36．大城市往往人口密集，城市绿化在健康人民群众肺方面发挥着非常重要的作用，历史留给我们城市里的大山拥有品种繁多的绿色植物更是无价之宝．改革开放以来，有的地方领导片面追求政绩，对森林资源野蛮开发受到严肃查处事件时有发生．2019年的春节后，广西某市林业管理部门在“绿水青山就是金山银山”理论的不断指引下，积极从外地引进甲、乙两种树苗，并对甲、乙两种树苗各抽测了10株树苗的高度（单位：厘米）数据如茎叶图：
（1）据茎叶图求甲、乙两种树苗的平均高度；
（2）据茎叶图，运用统计学知识分析比较甲、乙两种树苗高度整齐情况，并说明理由．

37．如图茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩．乙组记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以a表示．
（Ⅰ）若甲、乙两组的数学平均成绩相同，求a的值；
（Ⅱ）求乙组平均成绩超过甲组平均成绩的概率；
（Ⅲ）当a＝3时，试比较甲、乙两组同学数学成绩的方差的大小．（结论不要求证明）

38．某市共有600个农村淘宝服务站，随机抽取6个服务站统计其“双十一”期间的网购金额（单位：万元）的茎叶图如图所示，其中茎为十位数，叶为个位数．
（1）根据茎叶图计算样本数据的平均数；
（2）若网购金额（单位：万元）不小于18的服务站定义为优秀服务站，其余为非优秀服务站，根据茎叶图推断这600个农村淘宝服务站中有几个优秀服务站？
（3）从随机抽取的6个服务站中再任取2个作网购商品的调查，求至少有1个是优秀服务站的概率．

39．某市为了考核甲、乙两部门的工作情况，随机询问了50位市民．根据这50位市民
甲部门

乙部门
4
97
97665332110
98877766555554443332100
6655200
632220
3
4
5
6
7
8
9
10
59
0448
122456677789
011234688
00113449
123345
011456
000
（1）分别估 计该市的市民对甲、乙部门评分的中位数；
（2）分别估计该市的市民对甲、乙部门的评分高于90的可能性有多少？
（3）根据茎叶图分析该市的市民对甲、乙两部门的评价．

人教版2022届一轮复习打地基练习 茎叶图
参考答案与试题解析
一．选择题（共16小题）
1．国庆70周年庆典磅礴而又欢快的场景，仍历历在目．已知庆典中某省的游行花车需要用到某类花卉，而该类花卉有甲、乙两个品种，花车的设计团队对这两个品种进行了检测．现从两个品种中各抽测了10株的高度，得到如下茎叶图．下列描述正确的是（　　）

A．甲品种的平均高度大于乙品种的平均高度，且甲品种比乙品种长的整齐
B．甲品种的平均高度大于乙品种的平均高度，但乙品种比甲品种长的整齐
C．乙品种的平均高度大于甲品种的平均高度，且乙品种比甲品种长的整齐
D．乙品种的平均高度大于甲品种的平均高度，但甲品种比乙品种长的整齐
【分析】根据茎叶图所反映出数据的分布情况进行判断即可．
【解答】解：通过茎叶图数据可知：
甲品种的平均高度为：x甲=19+20+21+23+25+29+37+33+32+3110=27，
乙品种的平均高度为：x乙=10+14+10+26+27+30+44+46+46+4710=30，
所以乙品种的平均高度大于甲品种的平均高度，
但是乙品种的10株高度在分散，没有甲品种10株的高度集中，都集中在25左右，
故乙品种的平均高度大于甲品种的平均高度，但甲品种比乙品种长的整齐．
故选：D．
2．某同学进入高三后，4次月考的数学成绩的茎叶图如图，则该同学数学成绩的方差是（　　）

A．125 B．45 C．5 D．35
【分析】已知茎叶图，读出数据114，126，128，132，代入方差计算公式，可得答案．
【解答】解：已知某同学进入高二后，四次月考的数学成绩的茎叶图
可得该同学四次考试成绩分别为114，126，128，132，
则该同学数学成绩的平均数为114+126+128+1324=125，
方差=14[（114﹣125）2+（126﹣125）2+（128﹣125）2+（132﹣125）2]＝45．
故选：B．
3．如图是2013年中央电视台举办的挑战主持人大赛上，七位评委为某选手打出的分数的茎叶统计图，去掉一个最高分和一个最低分后，所剩数据的平均数和方差分别为（　　）

A．85，1.6 B．84，4 C．84，1.6 D．85，4
【分析】去掉一个最高分和一个最低分后，所剩数据为84，84，86，84，87，由此能求出所剩数据的平均数和方差．
【解答】解：去掉一个最高分和一个最低分后，所剩数据为84，84，86，84，87，
∴所剩数据的平均数为：x=15(84+84+86+84+87)=85．
所剩数据的方差为：S2=15[（84﹣85）2+（84﹣85）2+（86﹣85）2+（84﹣85）2+（87﹣85）2]＝1.6．
故选：A．
4．如图是某运动员在某个赛季得分的茎叶图统计表，则该运动员得分的中位数是（　　）

A．2 B．24 C．23 D．26
【分析】利用茎叶图和中位数的定义求解．
【解答】解：由茎叶图知，运动员在某个赛季得分为：
12，15，22，23，25，26，31，
∴该运动员得分的中位数为：23．
故选：C．
5．某超市抽取13袋袋装食用盐，对其质量（单位：g）进行统计，得到如图茎叶图，若从这13袋食用盐中随机选取1袋，则该袋食用盐的质量在[499，501]内的概率为（　　）

A．513 B．613 C．713 D．813
【分析】由题意，分析茎叶图，找出质量在[499，501]的个数，再求其概率即可．
【解答】解：这13袋中位于[499，501]的个数为6，
故所求概率为613．
故选：B．
6．某学校A、B两个班的数学兴趣小组在一次数学对抗赛中的成绩绘制茎叶图如下，

①A班数学兴趣小组的平均成绩高于B班的平均成绩；
②A班数学兴趣小组成绩的众数小于B班成绩的众数；
③A班数学兴趣小组成绩的极差小于B班成绩的极差；
④A班数学兴趣小组成绩的中位数大于B班成绩的中位数．
其中正确结论的编号为（　　）
A．①④ B．②③ C．②④ D．①③
【分析】对于①，根据已知中茎叶图中数据，代入平均数公式，可得答案．
对于②，众数是在一组数据中，出现次数最多的数，由图可得．
对于③，极差指的是这些数字分开得有多远，计算方法是：用其中最大的数减去最小的数即可得解．
对于④，中位数是按顺序排列的一组数据中居于中间位置的数，注意：中位数和众数不同，众数指最多的数，众数有时不止一个，而中位数只能有一个．
【解答】解：对于①，由已知中的茎叶图可得：
xA=115（53+62+64+76+74+78+78+76+81+85+86+88+82+92+95）＝78，
xB=115（45+48+51+53+56+62+64+65+73+73+74+70+83+82+91）＝66，
可得：xA＞xB，故正确．
对于②，A班数学兴趣小组成绩的众数为：76，78，B班成绩的众数为73，故错误；
对于③，A班数学兴趣小组成绩的极差为：95﹣40＝55，大于B班成绩的极差为：91﹣45＝46，
B班成绩的极差小，故错误．
对于④，A班数学兴趣小组成绩的中位数为：78，大于B班成绩的中位数65，故正确．
故选：A．
7．图1是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到14次的考试成绩依次记为A1，A2，…，A14．图2是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是（　　）

A．7 B．8 C．9 D．10
【分析】根据流程图可知该算法表示统计14次考试成绩中大于等于90的人数，结合茎叶图可得答案．
【解答】解：分析程序中各变量、各语句的作用，
再根据流程图所示的顺序，可知：
该程序的作用是累加14次考试成绩超过90分的人数；
根据茎叶图的含义可得超过90分的人数为10个
故选：D．
8．随着移动互联网的发展，与餐饮美食相关的手机APP软件层出不穷．为调查某两家订餐软件的商家的服务情况，统计了它们订餐“送达时间”（时间：分钟），得到茎叶图如图所示，则（　　）

A．甲款APP送餐时间更稳定，中位数为26
B．甲款APP送餐时间更稳定，中位数为27
C．乙款APP送餐时间更稳定，中位数为31
D．乙款APP送餐时间更稳定，中位数为36
【分析】由茎叶图中数据分析两款APP送餐时间集中情况，从而得出正确的结论．
【解答】解：由茎叶图中数据知，乙款APP送餐时间大部分集中在30～40分钟之间，
甲款APP送餐时间相对比较分散，素养乙款APP送餐时间更稳定些．
乙款APP统计的送餐时间共有13个数据，
由小到大排列后处于中间的是36，所以中位数是36．
故选：D．
9．我市某高中从高三年级甲、乙两个班中各选出7名学生参加2018年全国高中数学联赛（河南初赛），他们取得的成绩（满分140分）的茎叶图如图所示，其中甲班学生成绩的中位数是81，乙班学生成绩的平均数是86，若正实数a，b满足a，G，b成等差数列且x，G，y成等比数列，则1a+4b的最小值为（　　）

A．49 B．2 C．94 D．9
【分析】由中位数和平均数的定义可得x，y的值，再由等差数列和等比数列中项的性质求得a+b＝4，利用基本不等式求出1a+4b的最小值．
【解答】解：甲班学生成绩的中位数是80+x＝81，得x＝1；
由茎叶图可知乙班学生的总分为76+80×3+90×3+（0+2+y+1+3+6）＝598+y，
乙班学生的平均分是86，且总分为86×7＝602，所以y＝4，
若正实数a、b满足：a，G，b成等差数列且x，G，y成等比数列，
则xy＝G2，2G＝a+b，即有a+b＝4，a＞0，b＞0，
则1a+4b=14（a+b）（1a+4b）=14（1+4+ba+4ab）≥14（5+2ba⋅4ab）=14×9=94，
当且仅当b＝2a=83时，1a+4b的最小值为94．
故选：C．
10．已知七位评委为某民族舞蹈参赛演员评定分数的茎叶图如图中左边为十位数，右边为个位数．去掉一个最高分和一个最低分，所剩数据的平均数和方差分别为（　　）

A．84，4.84 B．84，1.6 C．85，1.6 D．85，4
【分析】根据所给的茎叶图，看出七个数据，根据分数处理方法，去掉一个最高分93和一个最低分79后，把剩下的五个数字求出平均数和方差．
【解答】解：由茎叶图知，去掉一个最高分93和一个最低分79后，
所剩数据84，84，86，84，87的平均数为 84+84+86+84+875=85；
方差为 15[(84−85)2+(84−85)2+(86−85)2+(84−85)2+(87−85)2]=85．
故选：C．
11．近几年，我国农村电子商务发展迅速，使得农副产品能够有效地减少流通环节，降低流通成本，直接提高了农民的收益．某农村电商对一个月内每天的顾客人数进行了统计，得到样本的茎叶图（如图所示），则该样本的中位数、众数、极差分别是（　　）

A．46.5，48，60 B．47，48，60 C．46.5，48，55 D．46.5，51，60
【分析】利用茎叶图、中位数、众数、极差的定义直接求解．
【解答】解：由茎叶图得：
该样本的中位数为：46+472=46.5，
众数为：48，
极差为：72﹣12＝60．
故选：A．
12．如图茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩（单位：分）．则甲组数据的中位数，乙组数据的平均数分别为（　　）

A．12，15 B．15，15 C．15，15.9 D．15，16.8
【分析】根据茎叶图得出数据，分别计算即可．
【解答】解：由茎叶图得：
甲组数据为：
9，12，15，24，27，
乙组数据为：
8，15，18，19，24，
故甲组数据的中位数是15，
乙组数据的平均数是：8+15+18+19+245=16.8，
故选：D．
13．甲、乙两名篮球运动员最近五场比赛的得分如茎叶图所示，则（　　）

A．甲的中位数和平均数都比乙高
B．甲的中位数和平均数都比乙低
C．甲的中位数比乙的中位数高，但平均数比乙的平均数低
D．甲的中位数比乙的中位数低，但平均数比乙的平均数高
【分析】由茎叶图分别求出甲的中位数、平均数和乙的中位数、平均数，由此能求出甲的中位数和平均数都比乙低．
【解答】解：由茎叶图得：
甲的中位数是29，平均数为：15（25+28+29+31+32）＝29，
乙的中位数是30，平均数为：15（28+29+30+31+32）＝30，
∴甲的中位数和平均数都比乙低．
故选：B．
14．如图是某次比赛上七位评委为某选手打出的分数的茎叶图，若去掉一个最高分和最低分，则所剩数据的平均数为（　　）

A．84 B．85 C．86 D．87
【分析】由已知中的茎叶图，我们可以得到七位评委为某参赛选手打出的分数，及去掉一个最高分和一个最低分后的数据，代入平均数公式公式，即可得到所剩数据的平均数．
【解答】解：由已知的茎叶图可得七位评委为某参赛选手打出的分数为：79，84，84，86，84，87，93，
去掉一个最高分93和一个最低分79后，
所剩数据的平均数 x=84+84+86+84+875=85．
故选：B．
15．某社区安置了15个体温检测点，每个检测点每天检测的人数都是随机的，不受位置等因素影响，如图是由某天检测人数绘制的茎叶图，则某个检测点某天检测人数达145及以上的概率是（　　）

A．715 B．815 C．13 D．23
【分析】根据茎叶图中数据，计算所求的概率值即可．
【解答】解：由茎叶图中数据知，
在15个数据中，人数达到145及以上的有10个，
所以所求的概率为P=1015=23．
故选：D．
16．如图是8位学生的某次数学测试成绩的茎叶图，则下列说法正确的是（　　）

A．众数为7 B．极差为18
C．中位数是64.5 D．平均数是64
【分析】根据茎叶图中的数据，计算这组数据的中位数、众数、极差和平均数即可．
【解答】解：这组数据的众数是67，故A错误；
极差是75﹣58＝17，故B错误；
根据茎叶图中的数据知，这组数据的中位数是12×（62+67）＝64.5，故C正确；
平均数是 18×（58+59+61+62+67+67+71+75）＝65，故D错误．
故选：C．
二．多选题（共1小题）
17．某校举行学习党史知识比赛，甲、乙两个班各有10名同学参加，根据成绩绘制茎叶图如下，则（　　）

A．x甲＞x乙 B．x甲＜x乙 C．S2甲＜S2乙 D．S2甲＞S2乙
【分析】由茎叶图中的数据，分别计算甲班、乙班的平均分和方差，比较大小即可．
【解答】解：由茎叶图中的数据，计算甲班平均分为x甲=110×（73+74+77+82+84+85+88+88+94+95）＝84，
乙班平均分x乙=110×（66+68+68+68+74+76+77+86+88+89）＝76，
所以甲班的平均数大于乙班平均数，即x甲＞x乙；
计算甲班成绩的方差是s甲2=110×[（﹣11）2+（﹣10）2+（﹣7）2+（﹣2）2+02+12+42+42+102+112]＝52.8；
乙班成绩的方差是s乙2=110×[（﹣10）2+（﹣8）2+（﹣8）2+（﹣8）2+（﹣2）2+02+12+102+122+132]＝62；
所有甲的方差小于乙的方差，即s甲2＜s乙2．
故选：AC．
三．填空题（共17小题）
18．为调动我市学生参与课外阅读的积极性，我市制定了《进一步加强中小学课外阅读指导的实施方案》，有序组织学生开展课外阅读活动．某校语文老师在班里开展了一次诗词默写比赛，班里40名学生得分数据的茎叶图如图．若规定得分不低于85分的学生得到“诗词达人的”称号，低于85分且不低于70分的学生得到“诗词能手”的称号，其他学生得到“诗词爱好者”的称号．根据该次比赛的成绩，按照称号的不同，进行分层抽样抽选15名学生，则抽选的学生中获得“诗词能手”称号的人数为　6人　．

【分析】根据茎叶图中数据，按分层抽样原理抽选即可．
【解答】解：40名学生得分在低于85分且不低于70分的学生有16人，可或“诗词能手”称号；
按分层抽样抽选15名学生，抽选的学生中获得“诗词能手”称号的人数为15×1640=6（人）．
故答案为：6人．
19．如图所示的茎叶图记录了甲乙两位射箭运动员的5次比赛成绩（单位：环），若两位运动员平均成绩相同，则成绩较为稳定（方差较小）的那位运动员成绩的方差为　2　．

【分析】本题考查的是数据的稳定程度与茎叶图形状的关系，茎叶图中各组数据若大部分集中在某条线上或方差越小表示该组数据越稳定．
【解答】解：有题意可得：两位运动员平均成绩相同，
即88+89+90+91+90+x5=87+89+90+91+935=90，
可得x＝2，
所以S甲2=(88−90)2+(89−90)2+(90−90)2+(91−90)2+(92−90)25=2；
S乙2=(87−90)2+(89−90)2+(90−90)2+(91−90)2+(93−90)25=4；
所以S甲2＜S乙2
则成绩较为稳定（方差较小）的那位运动员成绩的方差为2，
故答案为：2，
20．甲、乙两名学生的六次数学测验成绩（百分制）的茎叶图如图所示．
①甲同学成绩的中位数小于乙同学成绩的中位数；
②甲同学的平均分比乙同学的平均分高；
③甲同学的平均分比乙同学的平均分低；
④甲同学成绩的方差小于乙同学成绩的方差．
上面说法正确的是 　①③④　．

【分析】根据茎叶图中的数据，对题目中的命题进行分析、判断正误即可．
【解答】解：根据茎叶图中数据知，
对于①，甲同学成绩的中位数是12×（80+82）＝81，乙同学成绩的中位数是12×（87+88）＝87.5，
所以甲的中位数小于乙的中位数，①正确；
对于②，甲同学的平均分为16×（72+76+80+82+86+90）＝81，
乙同学的平均分为16×（69+78+87+88+92+96）＝85，
所以甲同学的平均分比乙同学的平均分低，②错误；
对于③，甲同学的平均分比乙同学的平均分低，③正确；
对于④，计算甲的方差为16×[（﹣9）2+（﹣5）2+（﹣1）2+12+52+92]=1073，
乙的方差为16×[（﹣16）2+（﹣7）2+22+32+72+112]=2443，
所以甲的方差小于乙的方差，④正确．
所以正确的命题序号是①③④．
故答案为：①③④．
21．某学校开展了“国学”系列讲座活动，为了了解活动效果，用分层抽样的方法从高一年级所有学生中抽取10人进行国学素养测试，这10名同学的性别和测试成绩（百分制）的茎叶图如图所示．则男生成绩的75%分位数为　77.5　；已知高一年级中男生总数为80人，试估计高一年级学生总数为　200　．

【分析】根据75%分位数的求法，结合题中数据，即可得到答案；根据分层抽样的定义，即可求得高一年级学生总数．
【解答】解：将男生成绩从小到大排列可得：64、76、77、78，共4个数据，且4×75%＝3，所以男生成绩的75%分位数为77+782=77.5．
设高一年级学生总数为n，
因为用分层抽样的方法抽取10人中，男生有4人，且高一年级中男生总数为80人，
所以410=80n，解得n＝200．
故答案是：77.5；200．
22．随机抽取某班10名同学，测量他们的身高（单位：cm）获得身高数据的茎叶图（如图），则这个班的众数为　168，179　，极差　24　．

【分析】由众数和极差的定义求值即可．
【解答】解：这个班的众数为：168，179，
极差为：182﹣158＝24．
故答案为：168，179，24．
23．如图茎叶图记录了甲、乙两组各5名工人某日的产量数据（单位：件），若这两组数据的中位数和平均数都相等，则x+y的值为　12　．

【分析】由已知有中这两组数据的中位数相等，且平均值也相等，可得x，y的值．
【解答】解：由已知中甲组数据：43，51，56，64，60+x；的中位数为56，
故乙组数据：45，53，50+y，59，67；的中位数也为65，即y＝6，
将y＝6，代入乙组可得乙组数据的平均数为：56，
这两组数据的平均值也相等，故x＝6，
所以：x+y＝6+6＝12；
故答案为：12．
24．如图所示的茎叶图记录了甲、乙两位学生5次体育测试的成绩，若这两组数据的平均值等，极差也相等，则学生乙体育测试的最高成绩为　77　．

【分析】由平均值相等得56+65+62+74+70+x5=59+61+67+65+70+y5解得y﹣x＝5，又知道极差相等，因为y﹣x＝5，所以x≤4，所以74﹣56＝70+y﹣59，解方程即可．
【解答】解：依题意，由平均值相等得56+65+62+74+70+x5=59+61+67+65+70+y5，解得y﹣x＝5，
又知道极差相等，因为y﹣x＝5，所以x≤4，
所以74﹣56＝70+y﹣59，解得y＝7，
所以学生乙体育测试的最高成绩为77，
故答案为：77．
25．从某工厂生产线上随机抽取16件零件，测量其内径数据从小到大依次排列如下（单位：mm）：1.12，1.15，1.21，1.23，1.25，1.25，1.26，1.30，1.30，1.32，1.34，1.35，1.37，1.38，1.41，1.42．据此可估计该生产线上大约有25%的零件内径小于等于　1.23　mm，大约有30%的零件内径大于　1.35　mm．
【分析】利用16×25%＝4，16×30%＝4.8，据此可估计该生产线上大约有25%的零件内径小于等于1.23mm，大约有30%的零件内径大于1.35mm．
【解答】解：从某工厂生产线上随机抽取16件零件，
测量其内径数据从小到大依次排列如下（单位：mm）：
1.12，1.15，1.21，1.23，1.25，1.25，1.26，1.30，1.30，1.32，1.34，1.35，1.37，1.38，1.41，1.42．
16×25%＝4，
16×30%＝4.8，
据此可估计该生产线上大约有25%的零件内径小于等于1.23mm，
大约有30%的零件内径大于1.35mm．
故答案为：1.23，1.35．
26．从甲、乙两个班中各随机选出15名同学进行随堂测验，成绩的茎叶图如图所示，则甲、乙两班的最高成绩分别是　96　，　92　.从图中看，　乙　班的平均成绩较高．

【分析】由茎叶图的概念可知甲乙两班的最高分，由成绩的集中区域可判断哪个班的平均成绩更高．
【解答】解：由茎叶图可知，甲班的最高分是96，乙班的最高分是92．
甲班的成绩集中在（60，80）内，乙班的成绩集中在（70，90）内，故乙班的平均成绩较高．
故答案为：96；92；乙．
27．一次体操比赛中，7位裁判为某运动员打出的分数如茎叶图所示（其中茎表示十位数，叶表示个位数），去掉一个最高分和一个最低分后，剩余数据的平均数为　89　．

【分析】根据茎叶图写出这7个数据，计算去掉一个最高分和一个最低分后剩余数据的平均数．
【解答】解：根据茎叶图知，这7个数据从小到大排列为：79，86，87，90，91，91，92；
去掉一个最高分92，一个最低分79，剩余数据的平均数为
x=15×（86+87+90+91+91）＝89．
故答案为：89．
28．甲、乙两位同学高三8次物理模拟考试成绩如图所示，甲同学的平均成绩与乙同学的众数相等，则m＝　5　．

【分析】由茎叶图求出甲同学的平均成绩和乙同学的众数，列方程求出m的值．
【解答】解：由茎叶图知，甲同学的平均成绩与乙同学的众数相等，
即18×（73+79+82+85+80+m+83+92+93）＝84，
解得m＝5．
故答案为：5．
29．在某社区举行的“讲文明，树新风”答题竞赛中，根据甲、乙两组选手的成绩，绘制的茎叶图如图所示，
甲组成绩的25%分位数为　70　；设甲、乙两组成的方差分别为s甲2，s乙2，那么s甲2　＞　s乙2．（填“＞”或“＜”或“＝”）

【分析】由茎叶图得甲组成绩从小到大排列，由25%×12＝3，得到甲组成绩的25%分位数为第3个数和第4个数的平均数，由茎叶图得甲组成绩相对分散，乙组成绩相对集中，从而s甲2＞s乙2．
【解答】解：由茎叶图得甲组成绩从小到大为65，67，69，71，75，77，80，83，85，89，93，95，
25%×12＝3，
∴69+712=70，
由茎叶图得甲组成绩相对分散，乙组成绩相对集中，
∴s甲2＞s乙2．
故答案为：70，＞．
30．甲、乙两位同学的5次考试成绩如茎叶图所示，则成绩较稳定的那位学生成绩的方差为　2　．

【分析】利用茎叶图分别求出甲、乙二人的平均数、方差，由此能求出成绩较稳定的那位学生成绩的方差．
【解答】解：甲的平均数为x1=15（88+89+90+91+92）＝90，
甲的方差为S12=15[（88﹣90）2+（89﹣90）2+（90﹣90）2+（91﹣90）2+（92﹣90）2]＝2，
乙的平均数为x2=15（89+87+93+90+91）＝90，
乙的方差为S22=15[（89﹣90）2+（87﹣90）2+（93﹣90）2+（90﹣90）2+（91﹣90）2]＝4．
∴成绩较稳定的那位学生成绩的方差为2．
故答案为：2．
31．甲、乙两名篮球运动员在几场比赛中得分的茎叶图如图所示，则甲、乙两人在这几场比赛中得分的中位数之和为 　52　．

【分析】由已知中的茎叶图，分别求出甲、乙两人这几场比赛得分的中位数，可得答案．
【解答】解：由已知中的茎叶图可得：
甲、乙两人这几场比赛得分的中位数分别为：24和28，
甲、乙两人这几场比赛得分的中位数的和为：24+28＝52．
故答案是：52．
32．某次数学测验五位同学的成绩分布茎叶图如图，则这五位同学数学成绩的方差为　10　．

【分析】已知茎叶图，读出数据122，128，129，130，131，代入方差计算公式，可得答案．
【解答】解：由图可得这五位同学考试成绩分别为122，128，129，130，131；
则这五位同学数学成绩的平均数为：15（122+128+129+130+131）＝128，
方差=15[（122﹣128）2+（128﹣128）2+（129﹣128）2+（130﹣128）2+（131﹣128）2]＝10．
故答案为：10．
33．在某项技能测试中，甲乙两人的成绩（单位：分）记录在如图所示的茎叶图中，其中甲的某次成绩不清晰，用字母a代替．已知甲乙成绩的中位数相等，那么a的值为　2　．

【分析】由茎叶图求出乙的中位数，得出甲的中位数，从而求得a的值．
【解答】解：由茎叶图知，乙的成绩从小到大排列为：18，18，20，20，24，28，所以中位数是20；
所以甲的成绩按从低到高排列：16，18，18，20+a，24，28，
计算甲的中位数是12×（18+20+a）＝20，解得a＝2．
故答案为：2．
34．在某项技能测试中，甲乙两人的成绩（单位：分）记录在如图所示的茎叶图中，其中甲的某次成绩不清晰，用字母a代替．已知甲乙成绩的平均数相等，那么甲成绩的中位数为　21　．

【分析】根据平均数相等列方程求出a的值，再求甲的中位数．
【解答】解：由题意知，16(16+18+18+a+20+24+28)=16(18+18+20+20+24+28)，
解得a＝4．
所以甲的成绩按从低到高排列：16，18，18，24，24，28，
所以甲的中位数为18+242=21．
故答案为：21．
四．解答题（共5小题）
35．某电视台举办青年歌手大奖赛，有10名评委打分，已知甲、乙两名选手演唱后的打分情况如茎叶图所示：

（Ⅰ）从统计的角度，你认为甲与乙比较，演唱水平怎样？
（Ⅱ）现场有3名点评嘉宾A、B、C，每位选手可以从中选2位进行指导，若选手选每位点评嘉宾的可能性相等，求甲乙两选手选择的点评嘉宾恰重复一人的概率．
【分析】（Ⅰ）由茎叶图可得：X甲=87.5，X乙=86.7，X甲＞X乙，即可得出结论；
（Ⅱ）求出所有基本事件，其中，甲乙两选手选择的点评嘉宾恰重复一人包含6个基本事件，即可求出甲乙两选手选择的点评嘉宾恰重复一人的概率．
【解答】解：（Ⅰ）由茎叶图可得：X甲=87.5，X乙=86.7，X甲＞X乙，
所以甲演唱水平更高一点，但甲的方差较大，即评委对甲的水平认可存在较大的差异 …（5分）
（Ⅱ）依题意，共有9个基本事件：

其中，甲乙两选手选择的点评嘉宾恰重复一人包含6个基本事件．
所以，所求概率为P=69=23． …（12分）
36．大城市往往人口密集，城市绿化在健康人民群众肺方面发挥着非常重要的作用，历史留给我们城市里的大山拥有品种繁多的绿色植物更是无价之宝．改革开放以来，有的地方领导片面追求政绩，对森林资源野蛮开发受到严肃查处事件时有发生．2019年的春节后，广西某市林业管理部门在“绿水青山就是金山银山”理论的不断指引下，积极从外地引进甲、乙两种树苗，并对甲、乙两种树苗各抽测了10株树苗的高度（单位：厘米）数据如茎叶图：
（1）据茎叶图求甲、乙两种树苗的平均高度；
（2）据茎叶图，运用统计学知识分析比较甲、乙两种树苗高度整齐情况，并说明理由．

【分析】本题考查的是数据的稳定程度与茎叶图形状的关系，茎叶图中各组数据若大部分集中在某条线上，表示该组数据越稳定．
【解答】解：（1）如茎叶图数据分析，预估甲种树苗的平均高度x甲=19+21+20+29+23+25+37+31+32+3310=27（厘米），
预估乙种树苗的平均高度x乙=10+14+10+27+26+30+47+46+44+4610=30（厘米）；
（2）由茎叶图分析值甲种树苗高度较为集中，乙种树苗高度较为分散，
所以甲种树苗将会长得比较整齐，乙种树苗将会长得参差不齐．
37．如图茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩．乙组记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以a表示．
（Ⅰ）若甲、乙两组的数学平均成绩相同，求a的值；
（Ⅱ）求乙组平均成绩超过甲组平均成绩的概率；
（Ⅲ）当a＝3时，试比较甲、乙两组同学数学成绩的方差的大小．（结论不要求证明）

【分析】（Ⅰ）直接由甲、乙两个小组的数学平均成绩相等列式求解a的值；
（Ⅱ）由（Ⅰ）中求得的结果可得，当a＝2，…，9时，乙组平均成绩超过甲组平均成绩，然后由古典概率模型概率计算公式求概率；
（Ⅲ）直接计算方差，然后比较大小．
【解答】解：（Ⅰ）由甲、乙两个小组的数学平均成绩相等，得13（88+92+92）=13[90+91+（90+a）]，
解得a＝1；
（Ⅱ）设“乙组平均成绩超过甲组平均成绩”为事件A，
a的取值有：0，1，2，…，9共有10种可能．
由（Ⅰ）可知，当a＝1时甲、乙两个小组的数学平均成绩相同，
∴当a＝2，…，9时，乙组平均成绩超过甲组平均成绩，共有8种可能．
∴乙组平均成绩超过甲组平均成绩的概率P（A）=810=45；
（Ⅲ）当a＝3时，x甲=13（88+92+92）=2723，x乙=13（90+91+93）=2743，
所以s甲2=(88−2723)2+(92−2723)2+(92−2723)23=329，
s乙2=(90−2743)2+(91−2743)2+(93−2743)23=149，
因为329＞149，所以甲组同学数学成绩的方差比乙组同学数学成绩的方差大．
38．某市共有600个农村淘宝服务站，随机抽取6个服务站统计其“双十一”期间的网购金额（单位：万元）的茎叶图如图所示，其中茎为十位数，叶为个位数．
（1）根据茎叶图计算样本数据的平均数；
（2）若网购金额（单位：万元）不小于18的服务站定义为优秀服务站，其余为非优秀服务站，根据茎叶图推断这600个农村淘宝服务站中有几个优秀服务站？
（3）从随机抽取的6个服务站中再任取2个作网购商品的调查，求至少有1个是优秀服务站的概率．

【分析】（1）结合茎叶图求出数据的平均数即可；
（2）根据概率值，求出优秀服务站的个数即可；
（3）分别列举出所有的基本事件以及满足条件的事件，作商求出概率即可．
【解答】解：（1）样本数据的平均数x=16（8+9+15+16+18+24）＝15．………………（4分）
（2）样本中优秀服务站有2个，概率为26=13，
由此估计这600个村级服务站中有600×13=200个优秀服务站． ………………（8分）
（3）样本中优秀服务站有2个，分别记为a1，a2，
非优秀服务站有4个，分别记为b1，b2，b3，b4，
从随机抽取的6个村级服务站中再任取2个的可能情况有：
（a1，a2），（a1，b1），（a1，b2），（a1，b3），（a1，b4），
（a2，b1），（a2，b2），（a2，b3），（a2，b4），
（b1，b2），（b1，b3），（b1，b4），
（b2，b3），（b2，b3），
（b3，b4）共15种，且它们是等可能的．……………………（12分）
记“至少有1个是优秀服务站”为事件A，则事件A包含的可能情况有：
（a1，a2），（a1，b1），（a1，b2），（a1，b3），（a1，b4），
（a2，b1），（a2，b2），（a2，b3），（a2，b4），
共9种情况，……………………（14分）
所以P（A）=915=35，
答：至少有1个是优秀服务站的概率为35．……………………（16分）
39．某市为了考核甲、乙两部门的工作情况，随机询问了50位市民．根据这50位市民
甲部门

乙部门
4
97
97665332110
98877766555554443332100
6655200
632220
3
4
5
6
7
8
9
10
59
0448
122456677789
011234688
00113449
123345
011456
000
（1）分别估 计该市的市民对甲、乙部门评分的中位数；
（2）分别估计该市的市民对甲、乙部门的评分高于90的可能性有多少？
（3）根据茎叶图分析该市的市民对甲、乙两部门的评价．
【分析】（1）注意到两组数字是有序排列的，50个数的中位数为第25，26两个数．
（2）甲部门评分数高于90共有5个、乙部门评分数高于90共有8个，从而用频率估计概率；
（3）由中位数及标准差分析即可．
【解答】解：（1）两组数字是有序排列的，50个数的中位数为第25，26两个数．
由给出的数据可知道，市民对甲部门评分的中位数为75+752=75；
对乙部门评分的中位数为66+682=67；
所以，市民对甲、乙两部门评分的中位数分别为75，67．
（2）甲部门评分数高于90共有5个、乙部门评分数高于90共有8个，
因此，估计市民对甲、乙部门的评分大于90的概率分别为p甲=550=0.1，p乙=850=0.16，
所以，市民对甲、乙部门的评分大于90的可能性分别为0.1，0.16．
（3）由所给茎叶图知，市民对甲部门的评分的中位数高于对乙部门评分的中位数．
而且由茎叶图可以大致看出对甲部门的评分标准差要小于对乙部门评分的标准差，
说明该市民对甲部门的评分较高、评价较为一致，对乙部门的评价较低，评价差异较大．