初中数学北师大版八年级上册第一章 勾股定理综合与测试优质复习课件ppt

这是一份初中数学北师大版八年级上册第一章 勾股定理综合与测试优质复习课件ppt，共23页。PPT课件主要包含了常用勾股数，共8组，勾股定理，“勾股定理”的作用，回顾一长度，c2b2-a2，∴c2402，∴c40，回顾二面积，等面积法等内容，欢迎下载使用。

3n，4n，5n(n为正整数）
1、熟记勾股定理及勾股数内容，并能规范运用；(重点)2、掌握“等面积法”的运用；(重点)3、理解并掌握“方程思想”；(难点)4、掌握“SA+SB=SC”公式，并能灵活运用；(重点)
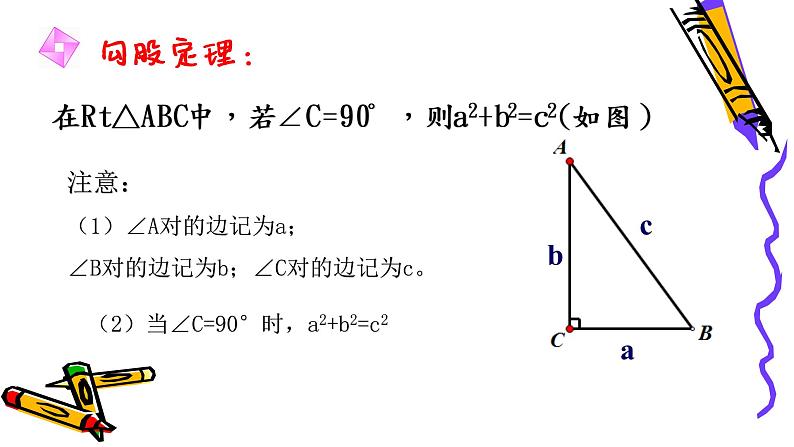
在Rt△ABC中，若∠C=90°，则a2+b2=c2(如图）
注意：（1）∠A对的边记为a；∠B对的边记为b；∠C对的边记为c。
（2）当∠C=90°时，a2+b2=c2
能解决图形中有关”长度、面积、距离”等数量问题；
在Rt△ABC中，AB=c,BC=a,AC=b,∠B=90°.(1)已知a=9，b=41,求c;
解：在Rt△ABC中，∠B=90°由勾股定理得
（2）已知a:c=3:4,且b=10,求a,c
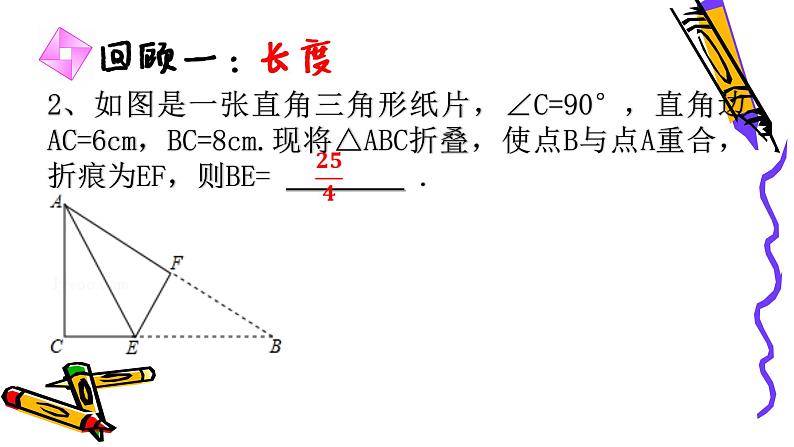
2、如图是一张直角三角形纸片，∠C=90°，直角边AC=6cm，BC=8cm.现将△ABC折叠，使点B与点A重合，折痕为EF，则BE= .
【例1】如图，已知在△ABC中，∠ACB=90°，AB=5cm，BC=3cm，CD⊥AB于D，求CD的长。
【例2】如图，在Rt△ABC中，∠B=90°，AB=7，BC=24，若在△ABC内存在一点P到各边的距离相等，即PM=PN=PL，则点P到各边的距离是 ．
【例3】如图，△ABC中，AB=15cm，AC=13cm，BC=14cm，求△ABC的面积．
注意：当要找一些未知长度时，要设x
【例4】等腰三角形底边上的高为8，周长为32，求这个三角形的面积。
解：如图高为AD，设BD为X，则AB为（16-X），
由勾股定理得：X2+82=(16-X)2
即X2+64=256-32X+X2
∴ S∆ABC=BC•AD/2=2 •6 •8/2=48
1、如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使AC恰好落在斜边AB上，且点C与点E重合，则CD的长为（ ）
回顾三：折叠问题(方程）
A.2 B.3 C.4 D.5
已知，如图，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（　　）　　　A．6cm2B．8cm2　　　C．10cm2D．12cm2
（2019-2020郑州）如图，把长方形纸片ABCD折叠，使其对角顶点C与A重合．若长方形的长BC为8，宽AB为4，则折痕EF的长度为（　　）
回顾四：毕氏图形再探究
两个小的面积之和等于最大的面积
【例1】下列三个图中字母B所代表图形面积都相同，面积是( )A．12 B．13 C．144 D．194
【例2】如图，已知半圆A的面积是3，半圆B的面积是4，则半圆C的面积是_______.
【例3】在 ， ,AC=3,BC=4分别以各边为直径作半圆，则阴影部分面积是多少 ？
如图，直线l上有三个正方形a，b，c，若a，c的面积分别为3和4，则b的面积为 . 　
【变式】在直线l上依次摆放着七个正方形（如图）；已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1+S2+S3+S4= ；