第6讲 二次函数中的双参数问题-2022年新高考数学二轮专题突破精练

第6讲 二次函数中的双参数问题

一．选择题（共3小题）

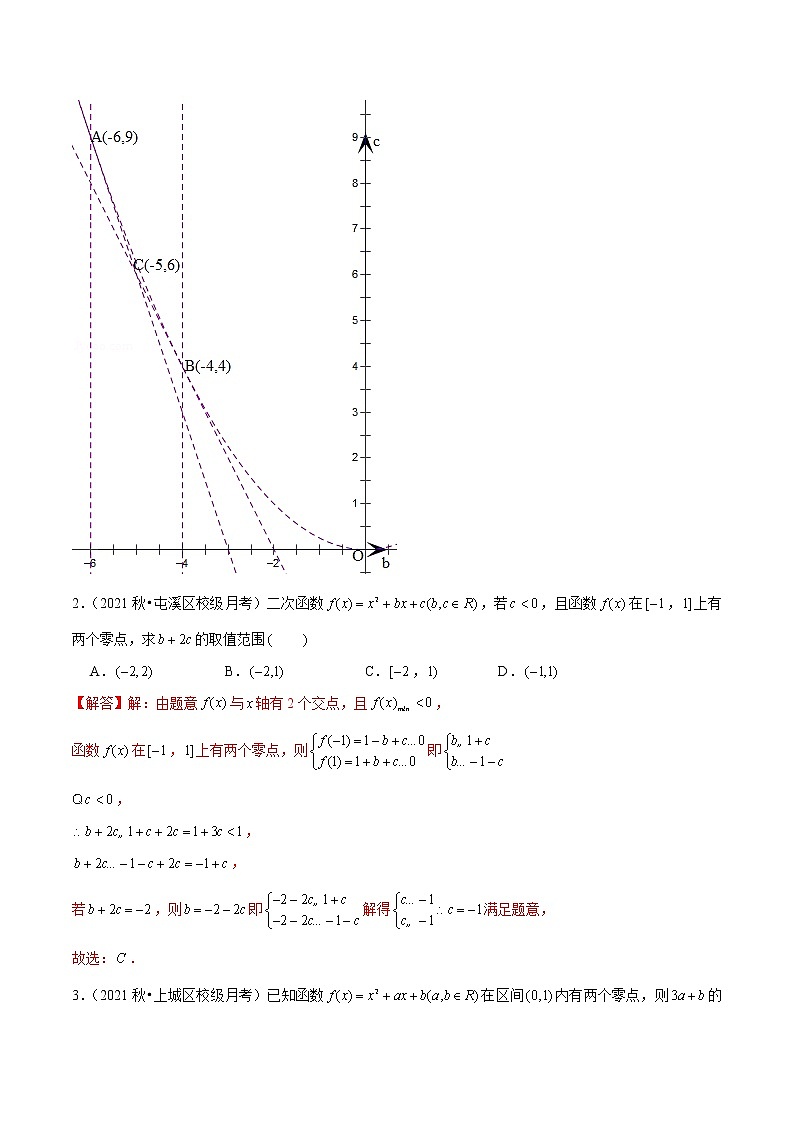
1．（2021春•湖州期中）已知二次函数，若在区间上有两个零点，则的取值范围为　　

A． B． C．， D．，

2．（2021秋•屯溪区校级月考）二次函数，若，且函数在，上有两个零点，求的取值范围　　

A． B． C．， D．

3．（2021秋•上城区校级月考）已知函数在区间内有两个零点，则的取值范围是　　

A． B． C． D．

二．填空题（共11小题）

4．（2021秋•灌云县校级期中）已知函数，，满足，（1），方程在区间上有两个实数根，则实数的取值范围为　　．

5．（2021春•沛县校级月考）若函数、在区间上有两个零点，则的取值范围是　　．

6．（2021•镇海区校级模拟）若函数在，上有零点，则的最小值为　　．

7．（2021•绍兴一模）已知，且，函数在，上至少存在一个零点，则的取值范围为　　．

8．（2021秋•西湖区校级期中）已知函数在，上存在零点，且对任意的，，，则的取值范围为　　．

9．已知关于的方程，在，上有实根，且，则的最大值为　 　．

10．（2021春•宁波期末）已知函数在区间，上有零点，则的最大值是　 　．

11．（2021•湖州模拟）已知关于的方程在，上有实数根，，则的取值范围是　　．

12．（2021秋•海陵区校级期末）设，为整数，方程在区间内有两个不同的根，则的最小值为　　．

13．设，为整数．方程在区间上有两个不同的根，则的取值范围是　　．

14．（2021•浙江模拟）设，，，对任意满足的实数，都有，则的最大可能值为　 　．

三．解答题（共8小题）

15．已知，，二次函数．

对任意的实数，存在，，使得，求正数的取值范围；

（2）若在上与轴有两个不同的交点，求的取值范围．

16．（2014秋•乐清市校级月考）已知二次函数．

（Ⅰ）当时，函数定义域和值域都是，，求的值；

（Ⅱ）若函数在区间上与轴有两个不同的交点，求的取值范围．

17．（2015•浙江）设函数．

（Ⅰ）当时，求函数在，上的最小值（a）的表达式．

（Ⅱ）已知函数在，上存在零点，，求的取值范围．

18．已知函数．

（1）（1）成立，求的取值范围；

（2）若在区间上有两个零点，求证：．

19．（2015秋•银川校级月考）已知二次函数．

（Ⅰ）若（2），（1），且不等式对所有，都成立，求函数的解析式；

（Ⅱ）若，且函数在，上有两个零点，求的取值范围；

（Ⅲ）在（Ⅰ）的条件下，当时，都有成立，求证：关于的方程有实根．

20．（2021秋•长安区校级月考）已知二次函数．

若（2），且函数的值域为，，求函数的解析式；

（Ⅱ）若，且函数在，上有两个零点，求的取值范围．

21．已知二次函数

（1）若且方程有整数解，，试求：，的值；

（2）若在上与轴有两个不同的交点，求的取值范围；

（3）若时，，且在区间，上的最大值为1，试求的最大值与最小值．

22．（2015•杭州校级模拟）（Ⅰ）定义在上的奇函数，当时，．另一个函数的定义域为，，值域为，其中，，．在，上，．求，．

（Ⅱ），，二次函数在上与轴有两个不同的交点，求的取值范围．