2021年上海市静安高三一模数学试卷及答案

这是一份2021年上海市静安高三一模数学试卷及答案，共12页。试卷主要包含了01等内容，欢迎下载使用。
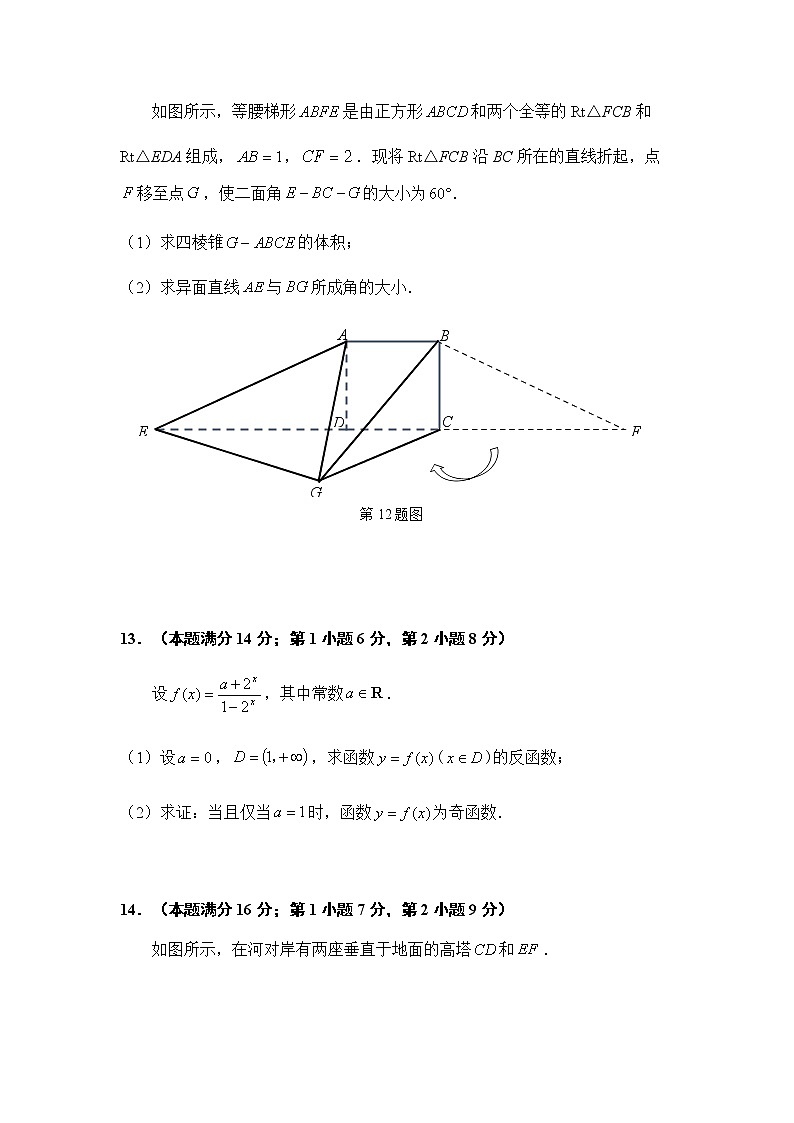
静安区2020学年第一学期教学质量检测                 高三数学试卷           2021.01一. 填空题（本大题共8题，每题6分，共48分）1．命题“若，则且”的逆否命题为   ▲   ．2．的二项展开式的常数项是   ▲   ．3．如图所示，弧长为，半径为1的扇形（及其内部）绕所在的直线旋转一周，所形成的几何体的表面积为   ▲  ．4．设是虚数单位，若是纯虚数，则实数   ▲  ．5．在△ABC中，，．是边上的中点，则的值为   ▲   ．6．某校的“希望工程”募捐小组在假期中进行了一次募捐活动．他们第一天得到15元，从第二天起，每一天收到的捐款数都比前一天多10元．要募捐到不少于1100元，这次募捐活动至少需要   ▲   天．（结果取整）7．某校开设9门选修课程，其中A，B，C三门课程由于上课时间相同，至多选一门，若规定每位学生选修4门，则一共有   ▲   种不同的选修方案．8. 如图所示，在平面直角坐标系中，动点   以每秒的角速度从点出发，沿半径为2的上半圆逆时针移动到，再以每秒的角速度从点沿半径为1的下半圆逆时针移动到坐标原点，则上述过程中动点的纵坐标关于时间的函数表达式为   ▲   ．二、选择题（本大题共3题，每题6分，共18分）9．若，，则下列不等式中必然成立的一个是         （    ）．A．； B．；  C．； D．．10．下列四个选项中正确的是                                （    ）．A．关于的方程（）的曲线是圆；B．设复数是两个不同的复数，实数，则关于复数的方程的所有解在复平面上所对应的点的轨迹是椭圆；C．设为两个不同的定点，为非零常数，若，则动点的轨迹为双曲线的一支；D．双曲线与椭圆有相同的焦点． 11．在平面直角坐标系中，、是位于不同象限的任意角，它们的终边交单位圆（圆心在坐标原点）于、两点．若、两点的纵坐标分别为正数、，且，则的最大值为          （    ）．A．； B．；        C．；        D．不存在．三、解答题（本大题共有5题，共84分）12．（本题满分14分，第1小题7分，第2小题满分7分）如图所示，等腰梯形是由正方形和两个全等的Rt△FCB和Rt△EDA组成，，．现将Rt△FCB沿BC所在的直线折起，点移至点，使二面角的大小为．（1）求四棱锥的体积；（2）求异面直线与所成角的大小．       13．（本题满分14分；第1小题6分，第2小题8分）设，其中常数．（1）设，，求函数()的反函数；（2）求证：当且仅当时，函数为奇函数． 14．（本题满分16分；第1小题7分，第2小题9分）如图所示，在河对岸有两座垂直于地面的高塔和．张明在只有量角器（可以测量从测量人出发的两条射线的夹角）和直尺（可测量步行可抵达的两点之间的直线距离）的条件下，为了计算塔的高度，他在点A测得点的仰角为，，又选择了相距100米的点，测得．（1）请你根据张明的测量数据求出塔CD高度；（2）在完成（1）的任务后，张明测得，并且又选择性地测量了两个角的大小（设为、）．据此，他计算出了两塔顶之间的距离DF．请问：①张明又测量了哪两个角？（写出一种测量方案即可）②他是如何用、表示出DF的？（写出过程和结论）          15．（本题满分19分，第1小题6分，第2小题6分，第3小题7分）个正数排成行列方阵，其中每一行从左至右成等差数列，每一列从上至下都是公比为同一个实数的等比数列．已知，，．（1）设，求数列的通项公式；（2）设，求证：()；（3）设，请用数学归纳法证明：．16．（本题满分21分，第1小题6分，第2小题7分，第3小题8分）如图所示，定点到定直线的距离．动点到定点的距离等于它到定直线距离的2倍．设动点的轨迹是曲线．（1）请以线段所在的直线为轴，以线段上的某一点为坐标原点，建立适当的平面直角坐标系，使得曲线经过坐标原点，并求曲线的方程；（2）请指出（1）中的曲线的如下两个性质：①范围；②对称性．并选择其一给予证明．（3）设（1）中的曲线除了经过坐标原点，还与轴交于另一点，经过点的直线交曲线于，两点，求证：．           静安区2020学年第一学期教学质量检测高三数学试卷答案与评分参考标准一.  1．若或，则    2．60；   3．；  4．；5. ；    6．14；    7．75；   8. 二、9．C； 10．D； 11．B．三、12．      解：（1）由已知，有所以         （1分）联结，由，，有①（1分）由有所以，②        （1分）由①②知，所以就是四棱锥的高     （1分）在Rt中，                            （1分）故，                            （2分）（2）取的中点，联结、，                         （1分）则，故既是与所成角或其补角.             （1分）在中，，,            （2分）则                                              （2分）故，异面直线与所成角的大小为.                  （1分）13．解：（1）由已知，设,得．             （2分）又，所以，函数()单调递增. （2分）故，，；                      （2分）（2）i)函数的定义域为．            （1分）若，，对于任意的，有．所以，是奇函数．                                 （3分）ii) 方法1：由是奇函数，有，解得．   （4分）方法2：若，则，，（否则），不是奇函数．                  （4分）方法3：若为奇函数，则，对于任意的，有，即，．即．．                              （4分）14．解：（1）在中，， （1分）由正弦定理，有，（3分）所以，米．   （2分）米．      （1分）（2）由（1）有米． 测得，．  （2分）                     由已知，有，，所以，，得． 所以，．（2分）在中，由余弦定理，有       （3分）米．（2分）【另解1】测得，．解得，，，．在中，由余弦定理，有米．（同样给分）【另解2】测得，．                    （2分）由已知，有，，所以，，得． 所以，．                                    （2分）在中，由余弦定理，有米．         （2分）米．                                   （1分）截取，则，米．  （2分）【另解3】测得，．                     （2分）由已知，有，，所以，，得． 解得，．                                     （2分）在中，由余弦定理，有米．          （2分）米．                                    （1分）截取，则，米．   （2分）             15．解：（1）由题意，数列是等差数列，设首项为，公差为，由，得解得，．                           （3分）故，数列的通项公式为．             （3分） （2）由（1）可得，再由已知，得，解得，由题意舍去．                   （3分）．由指数函数的性质，有()．                      （3分）（3）（i）当时，，等式成立．                       （1分）（ii）假设当时等式成立，即，     （1分）当时，，  等式成立．                                               （4分）根据（i）和（ii）可以断定，对任何的都成立.（1分）16．解：（1）在线段上取点，使得，以点为原点，以线段所在的直线为轴建立平面直角坐标系．        （2分）设动点的坐标为，则有，，由题意，有，整理得：． ①    （4分）（2）①范围：或，曲线位于直线与两侧．      （1分）②对称性：曲线关于成轴对称；                               （1分）曲线关于成轴对称；                              （1分）曲线关于成中心对称．                            （1分）范围证明：，                （3分）对称性证明：在方程①中，把换成，方程①不变，所以，曲线关于成轴对称；                             （1分）在方程①中，把换成，方程①不变，所以，曲线关于成轴对称；                            （1分）在方程①中，把换成，或把换成，方程①不变，所以，曲线关于成中心对称；                          （1分）（3）将代入，解得，（舍）．所以．                                           （1分）（i）若直线垂直于轴:将代入，解得，此时，、．所以，，．．                                （2分）（ii）若直线不垂直于轴: 设、，，．直线的方程为，将其代入，整理得，．                     （1分）所以，，．                   （1分）． （1分）． （1分）故，．                                          （1分）