初中浙教版3.4 一元一次不等式组教案及反思

这是一份初中浙教版3.4 一元一次不等式组教案及反思，共4页。
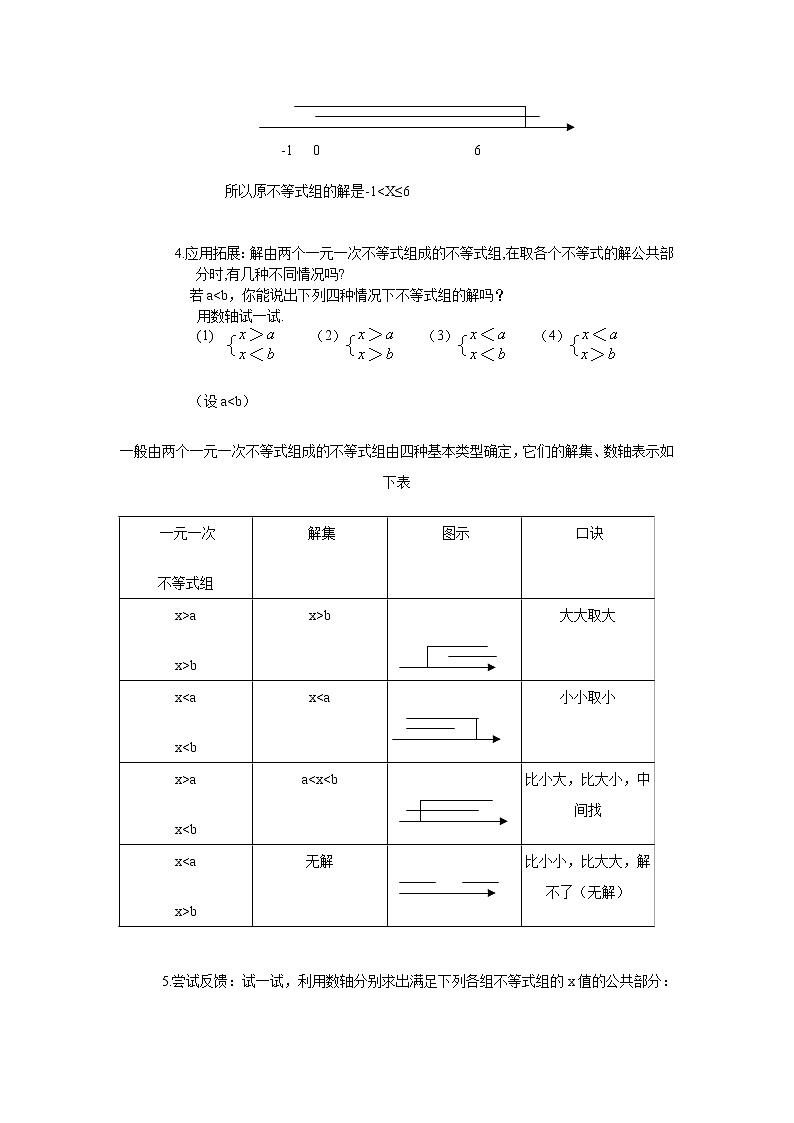
 3.4一元一次不等式组 1、理解一元一次不等式组的概念. 2、理解不等式组的解的概念．3、会解由两个一元一次不等式组成的不等式组，并会用数轴确定解. 4、培养学生类比推理能力．教学重点一元一次不等式组的解法.教学难点例2较为复杂，几乎包括了解一元一次不等式的全部步骤，是本节教学的难点，用数轴表示一元一次不等式组的解也是难点。         一.导入新课      1．想一想：某单位从超市购买了墨水笔和圆珠笔共15桶，所付金额超过570元，但不到580元。已知这两种笔每桶的单价为圆珠笔34.90元/支，墨水笔44.90元/支。设购买圆珠笔Ｘ桶，你能列出几个不等式？2．学生活动：找出已知条件，列出所有不等关系式，互相讨论，类推概念，鼓励学生通过观察，分析，补充解决问题。3．最后教师总结两个不等式。如设购买圆珠笔的桶数为Ｘ，则 ：二.探究新知1．一元一次不等式组：一般地，由几个同一个未知数的一元一次不等式所组成的一组不等式，叫做一元一次不等式组。像上面就是一元一次不等式组，再例如： 都是一元一次不等式组.2. 不等式组解的概念：组成不等式组的各个不等式的解的公共部分就是不等式组的解.当它们没有公共部分时.我们称这个不等式组无解.3.做一做：例1.解一元一次不等式组 解：解不等式①,  得: X>-1解不等式②,  得: X≤6把 ①  ②两个不等式的解表示在数轴上,如下图:                                  -1   0                      6                所以原不等式组的解是-1<X≤6       21世纪教育网21世纪教育网 4.应用拓展：解由两个一元一次不等式组成的不等式组,在取各个不等式的解公共部分时,有几种不同情况吗?          若a<b，你能说出下列四种情况下不等式组的解吗？           用数轴试一试.           (1)       （2）    （3）    （4）          （设a<b）一般由两个一元一次不等式组成的不等式组由四种基本类型确定，它们的解集、数轴表示如下表 一元一次不等式组 解集 图示 口诀x>ax>bx>b21世纪教育网大大取大x<ax<bx<a 小小取小x>ax<ba<x<b 比小大，比大小，中间找x<ax>b无解 比小小，比大大，解不了（无解）        5.尝试反馈：试一试，利用数轴分别求出满足下列各组不等式组的x值的公共部分：          (1)                   (2)             (3)                 (4)                                                    6．探索较复杂的不等式组的解法：例2. 解一元一次不等式组            解:由不等式①,去扩号得  3-5X>X-4X+2                 移项,整理得  -2X>-1   所以X<             解不等式②,去分母得  3X-2>10-2X                 移项,整理得  5X>12              所以X>            把①,②两个不等式的解表示在数轴上.                    0  1   2  3 所以原不等式组无解. 7.通过范例,帮助学生总结解一元一次不等式组的步骤:         (1)依次解各个一元一次不等式.         (2)把各个一元一次不等式的解分别表示在同一数轴上.         (3)根据解在数轴上的表示确定不等式组的解.21世纪教育网  三.巩固练习 （学生活动，与同伴交流自己的问题和解决问题的过程）1. 解下列一元一次不等式组:          (1)       (2)                                                   2. 分别求出本节开头问题中购买墨水笔和圆珠笔的桶数四．课堂小结         1．学生谈本节课的收获：优等生谈学到什么知识，上进生谈体会；21世纪教育网         2．教师小结：这节课主要学习了一元一次不等式组及不等式组的解的有关概念，要求会解有两个一元一次不等式组成的一元一次不等式组，并会用数轴确定解集；也可以利用口诀“大大取大，小小取小，比小大比大小取中间，比大大比小小无解”来求不等式组的解。请完成本课时对应练习！