初中浙教版2.3 用频率估计概率教学设计

这是一份初中浙教版2.3 用频率估计概率教学设计，共5页。教案主要包含了导入新课，探索新知，归纳小结等内容，欢迎下载使用。
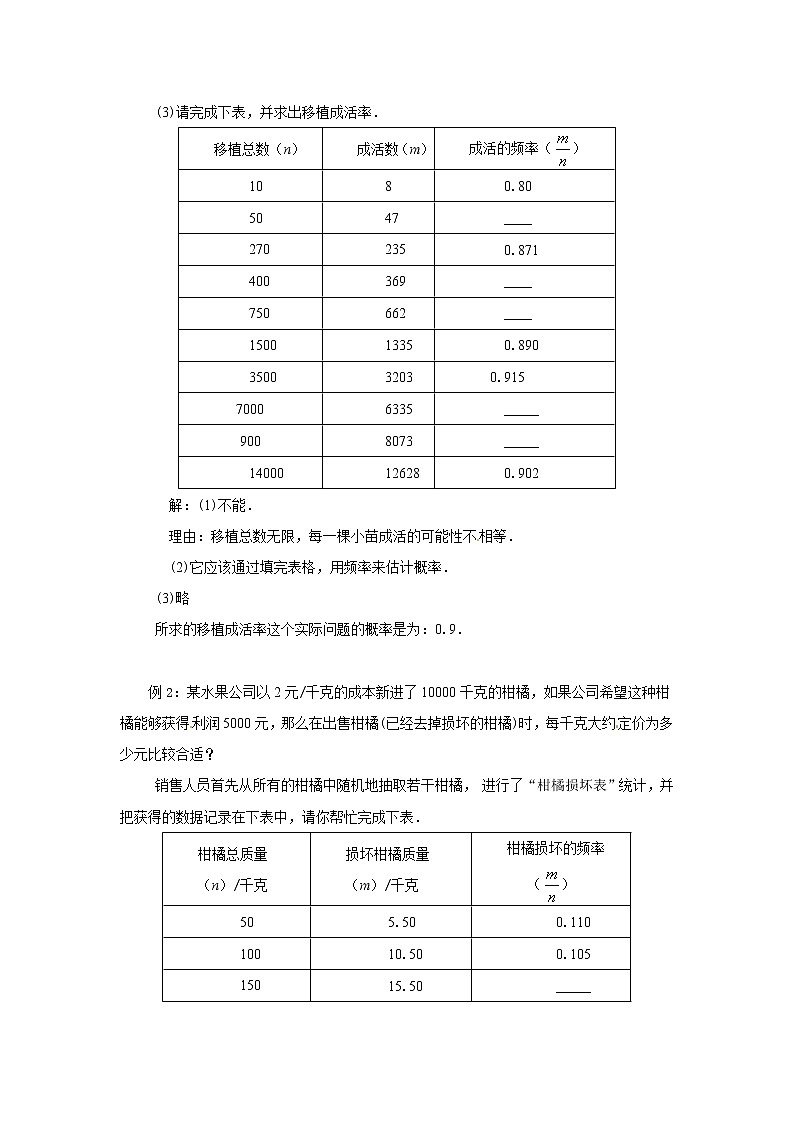
2.3 用频率估计概率1.理解每次试验可能结果不是有限个，或各种可能结果发生的可能性不相等时，用频率估计概率的方法；能应用模拟实验求概率及其它们的应用．2.通过复习列举法求概率的条件和方法，引入相反方向的：每次试验的所有可能结果不是有限个，或各种可能结果发生的可能性不相等时，利用频率求概率的方法，同时也介绍利用模拟试验求概率的方法．教学重点用频率估计概率的条件及方法.教学难点频率与概率的关系. 一、导入新课教师提出问题：周末市体育场有一场精彩的篮球比赛，老师手中只有一张球票，小强与小明都是班里的篮球迷，两人都想去.我很为难，真不知该把球给谁.请大家帮我想个办法来决定把球票给谁.学生：抓阄、抽签、猜拳、投硬币，……教师对同学的较好想法予以肯定.（学生肯定有许多较好的想法，在众多方法中推举出大家较认可的方法.如抓阄、投硬币）追问，为什么要用抓阄、投硬币的方法呢？ 由学生讨论：这样做公平.能保证小强与小明得到球票的可能性一样大在学生讨论发言后，教师评价归纳.用抛掷硬币的方法分配球票是个随机事件，尽管事先不能确定“正面朝上”还上“反面朝上”，但同学们很容易感觉到或猜到这两个随机事件发生的可能性是一样的，各占一半，所以小强、小明得到球票的可能性一样大.质疑：那么，这种直觉是否真的是正确的呢？引导学生以投掷壹元硬币为例，不妨动手做投掷硬币的试验来验证一下.说明：现实中不确定现象是大量存在的， 新课标指出：“学生数学学习内容应当是现实的、有意义、富有挑战的”，设置实际生活问题情境贴近学生的生活实际，很容易激发学生的学习热情，教师应对此予以肯定，并鼓励学生积极思考，为课堂教学营造民主和谐的气氛，也为下一步引导学生开展探索交流活动打下基础. 二、探索新知 例1：某林业部门要考查某种幼树在一定条件的移植成活率． (1)它能够用列举法求出吗？为什么？ (2)它应用什么方法求出？  (3)请完成下表，并求出移植成活率．移植总数（n）成活数（m）成活的频率（）     10    8     0.80     50    47     ____     270    235     0.871     400    369     ____     750    662     ____     1500    1335     0.890     3500    3203   0.9157000    6335     _____900    8073     _____     14000    12628     0.902   解：(1)不能．   理由：移植总数无限，每一棵小苗成活的可能性不相等．   (2)它应该通过填完表格，用频率来估计概率． (3)略 所求的移植成活率这个实际问题的概率是为：0.9． 例2：某水果公司以2元/千克的成本新进了10000千克的柑橘，如果公司希望这种柑橘能够获得利润5000元，那么在出售柑橘(已经去掉损坏的柑橘)时，每千克大约定价为多少元比较合适？ 销售人员首先从所有的柑橘中随机地抽取若干柑橘，进行了“柑橘损坏表”统计，并把获得的数据记录在下表中，请你帮忙完成下表．柑橘总质量（n）/千克损坏柑橘质量（m）/千克柑橘损坏的频率（）      50      5.50       0.110      100      10.50       0.105      150      15.50       _____      200      19.42       _____      250      24.25       _____      300      30.93       _____      350[来源:      35.32       _____      400      39.24       _____      450      44.57       _____      500      51.54       _____   解：从填完表格，我们可得，柑橘损坏的概率为0.1，则柑橘完成的概率为0.9．   因此：在10000千克柑橘中完好柑橘的质量为10000×0.9=9000千克．   完好柑橘的实际成本为：   =2.22(元/千克) www.xkb1.com   设每千克柑橘的销价为x元，则应有：   (x-2.22)×9000=5000   解得：x≈2.8   因此，出售柑橘时每千克大约定价为2.8元可获利润5000元．   例3：一个学习小组有6名男生3名女生，老师要从小组的学生中先后随机地抽取3人参加几项测试，并且每名学生都可被重复抽取，你能设计一种试验来估计“被抽取的3人中有2名男生1名女生”的概率吗？ 分析：因为要做从这9人中，抽取3人的试验确实工作量很大，为了简便这种试验，我们可用下面两种方法来简便． 1．取9张形状完全相同的卡片，在6张卡片上分别写上1～6的整数表示男生，在其余的3张卡片上分别写上7～9的整数表示女生，把9张卡片混合起来并洗均匀． 从卡片中放回的抽3次，随机抽取，每次抽取1张，并记录结果，经重复大量试验，就能够计算相关频率，估计出三人中两男一女的概率．  2．用计算器也能产生你指定的两个整数之间(包括这两个整数)的随机整数，也同样能够估计概率． 以上这两种试验我们把它称为模拟实验．从模拟实验中产生的一串串的数为“随机数”．  例4：在车站、街旁、旅游点、学校门口常常看到以下的博彩游戏：玩法（1）记分卡共20张，其中5分、10分各10张；（2）记分卡反放，每次任意摸10张，总分在下列分数中的可以得到与该分数对应的奖品；（3）每次摸奖付1元。分数100 95 90 85 80 75 70 65 60 55 50奖品彩电文曲星钢笔圆珠笔空门空门空门气球香皂计算器[来源:手表   奖品丰厚，围观者蠢蠢欲动，但也奇怪，有数十个人参加摸奖，摸到空门的居多，根本没有人摸到价值高的奖品，是偶数还是必然，你认为呢？以摸到100分为例说明．   分析：摸奖者摸10张卡片，总分在50至100之间，除了70、75、80三个分数没有外，其余的分数都有奖，并且奖品大都远远超过1元，所以人们觉得赢的机会非常大，可是事实恰恰相反，得到贵一点的奖品几乎没有人，是什么原因呢？    原来在50至100之间的11个分数中，摸10张卡总分最有可能是70、75、80，而相应的奖品是空的，其余分数虽然都有奖品，甚至在两边的得分可得到高额奖品，但这些分数很难得到． 解：是必然．理由：以摸到100分为例，需连续摸到10张卡片都是10分的，第一次摸到10分的机会是，再摸第二次摸到10分卡片的机会是，第三次摸到的卡片是10分的机会是，……依次类推，连续摸十次都是10分的机会只有，接近于二十万分之，以每次一元计算，需要近二十万元才能得到一台彩电! 三、归纳小结    1．用频率估计概率的条件及方法．    2．随机数的概念．    3．模拟实验的概念及它的各种方法．    4．应用以上的内容解决一些实际问题．请完成本课时对应练习！