数学第十单元 概率与统计初步10.5 总体与样本教案
展开章节
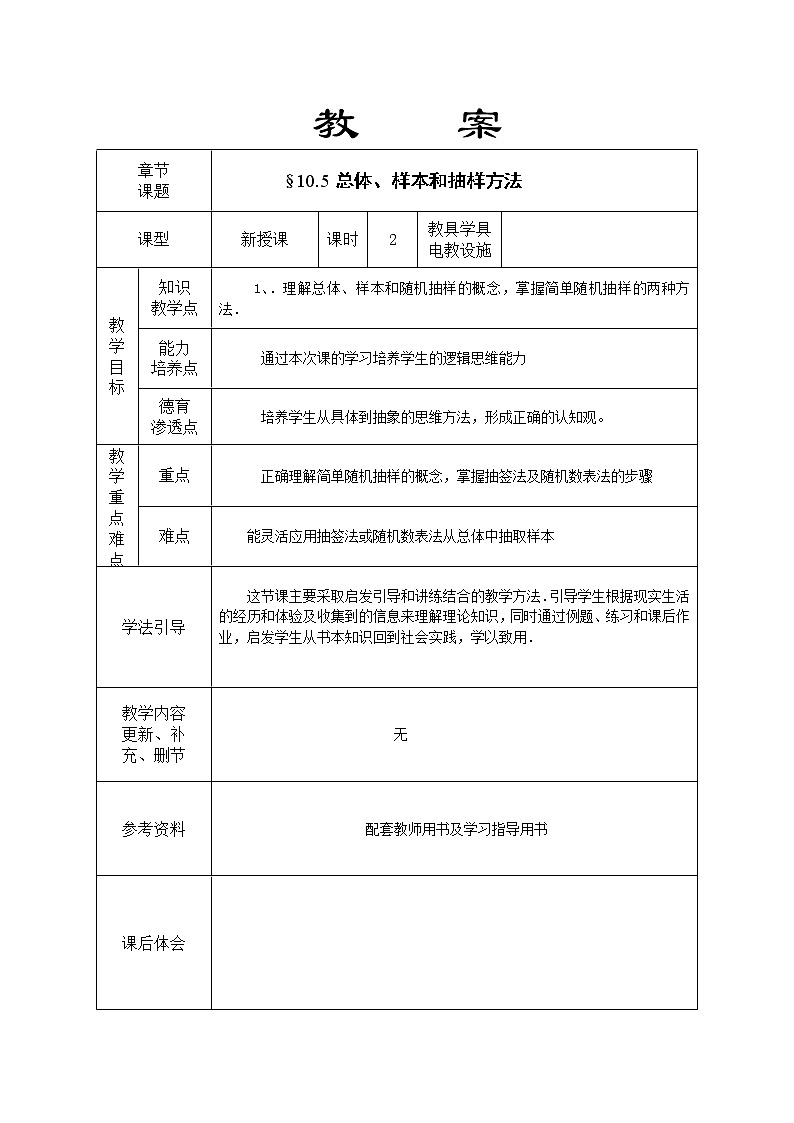
课题
§10.5总体、样本和抽样方法
课型
新授课
课时
2
教具学具电教设施
教学目标
知识
教学点
1、.理解总体、样本和随机抽样的概念,掌握简单随机抽样的两种方法.
能力
培养点
通过本次课的学习培养学生的逻辑思维能力
德育
渗透点
培养学生从具体到抽象的思维方法,形成正确的认知观。
教学重点难点
重点
正确理解简单随机抽样的概念,掌握抽签法及随机数表法的步骤
难点
能灵活应用抽签法或随机数表法从总体中抽取样本
学法引导
这节课主要采取启发引导和讲练结合的教学方法.引导学生根据现实生活的经历和体验及收集到的信息来理解理论知识,同时通过例题、练习和课后作业,启发学生从书本知识回到社会实践,学以致用.
教学内容
更新、补
充、删节
无
参考资料
配套教师用书及学习指导用书
课后体会
教 与 学 互 动 设 计
教 师 活 动 内 容
学生活动内容
时间
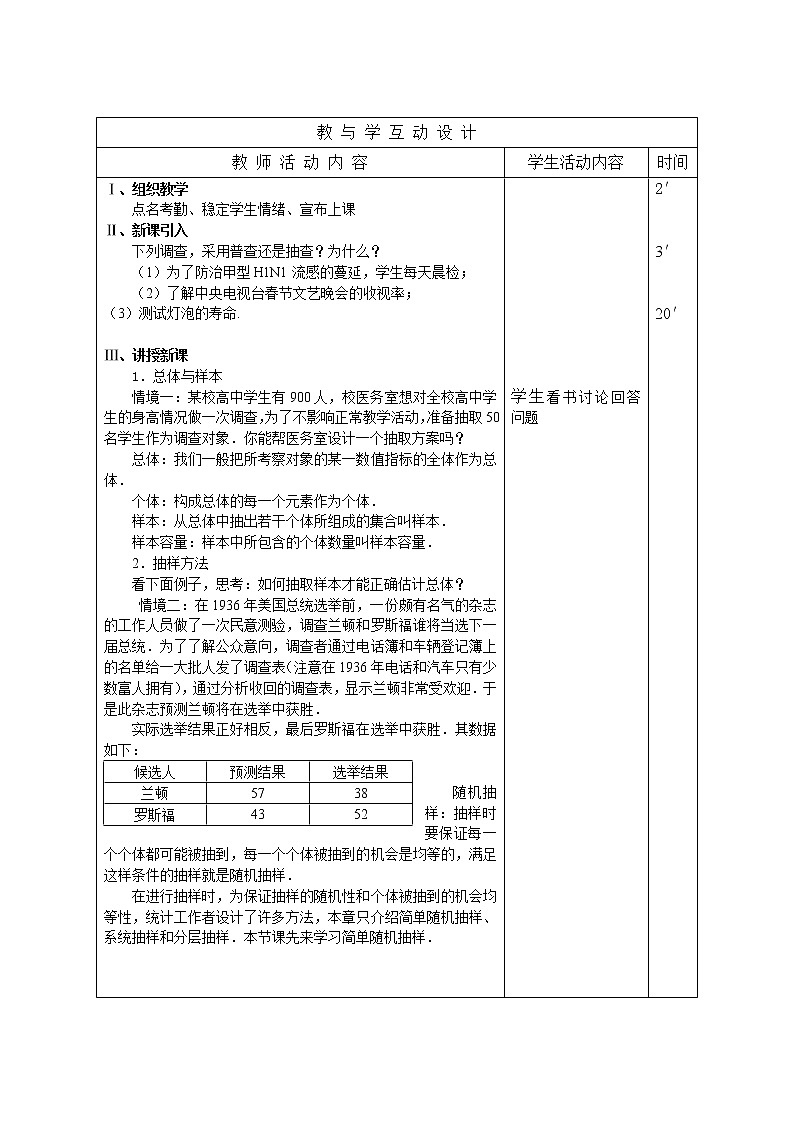
Ⅰ、组织教学
点名考勤、稳定学生情绪、宣布上课
Ⅱ、新课引入
下列调查,采用普查还是抽查?为什么?
(1)为了防治甲型H1N1流感的蔓延,学生每天晨检;
(2)了解中央电视台春节文艺晚会的收视率;
(3)测试灯泡的寿命.
Ⅲ、讲授新课
1.总体与样本
情境一:某校高中学生有900人,校医务室想对全校高中学生的身高情况做一次调查,为了不影响正常教学活动,准备抽取50名学生作为调查对象.你能帮医务室设计一个抽取方案吗?
总体:我们一般把所考察对象的某一数值指标的全体作为总体.
个体:构成总体的每一个元素作为个体.
样本:从总体中抽出若干个体所组成的集合叫样本.
样本容量:样本中所包含的个体数量叫样本容量.
2.抽样方法
看下面例子,思考:如何抽取样本才能正确估计总体?
情境二:在1936年美国总统选举前,一份颇有名气的杂志的工作人员做了一次民意测验,调查兰顿和罗斯福谁将当选下一届总统.为了了解公众意向,调查者通过电话簿和车辆登记簿上的名单给一大批人发了调查表(注意在1936年电话和汽车只有少数富人拥有),通过分析收回的调查表,显示兰顿非常受欢迎.于是此杂志预测兰顿将在选举中获胜.
实际选举结果正好相反,最后罗斯福在选举中获胜.其数据如下:
候选人
预测结果
选举结果
兰顿
57
38
罗斯福
43
52
随机抽样:抽样时要保证每一个个体都可能被抽到,每一个个体被抽到的机会是均等的,满足这样条件的抽样就是随机抽样.
在进行抽样时,为保证抽样的随机性和个体被抽到的机会均等性,统计工作者设计了许多方法,本章只介绍简单随机抽样、系统抽样和分层抽样.本节课先来学习简单随机抽样.
学生看书讨论回答问题
2′
3′
20′
教 与 学 互 动 设 计
教 师 活 动 内 容
学生活动内容
时间
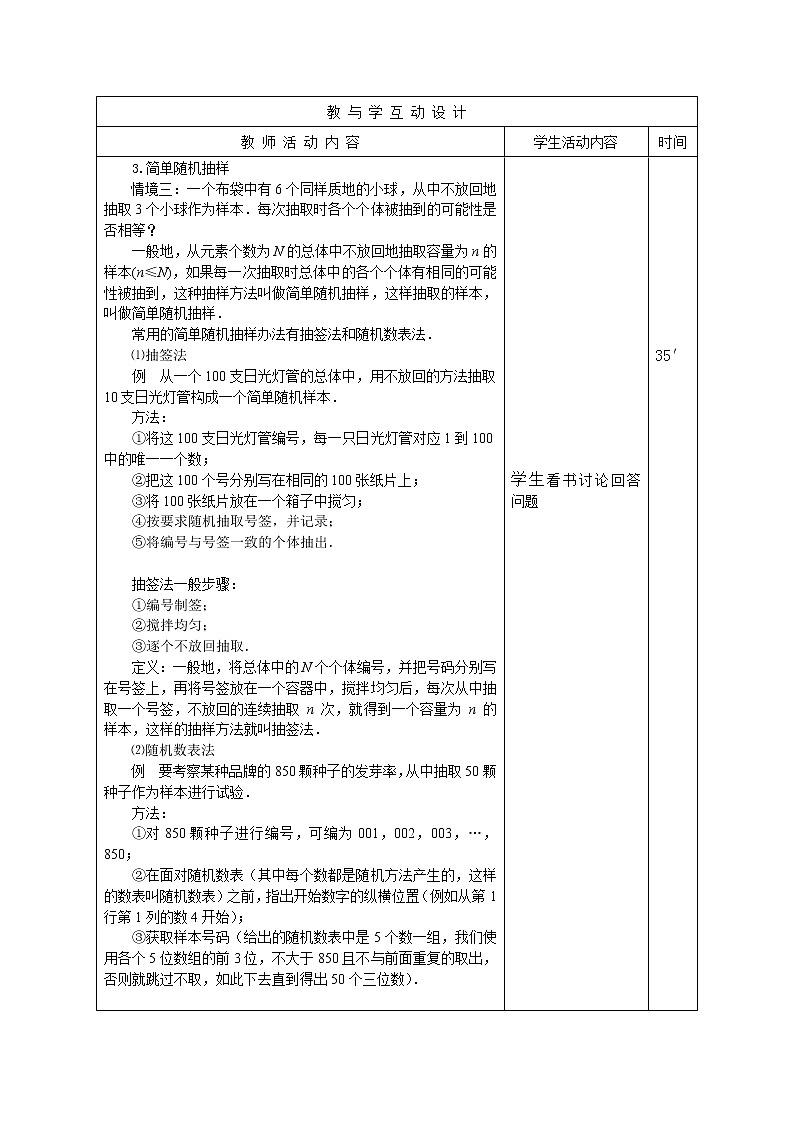
3.简单随机抽样
情境三:一个布袋中有6个同样质地的小球,从中不放回地抽取3个小球作为样本.每次抽取时各个个体被抽到的可能性是否相等?
一般地,从元素个数为N的总体中不放回地抽取容量为n的样本(n≤N),如果每一次抽取时总体中的各个个体有相同的可能性被抽到,这种抽样方法叫做简单随机抽样,这样抽取的样本,叫做简单随机抽样.
常用的简单随机抽样办法有抽签法和随机数表法.
⑴抽签法
例 从一个100支日光灯管的总体中,用不放回的方法抽取10支日光灯管构成一个简单随机样本.
方法:
①将这100支日光灯管编号,每一只日光灯管对应1到100中的唯一一个数;
②把这100个号分别写在相同的100张纸片上;
③将100张纸片放在一个箱子中搅匀;
④按要求随机抽取号签,并记录;
⑤将编号与号签一致的个体抽出.
抽签法一般步骤:
①编号制签;
②搅拌均匀;
③逐个不放回抽取.
定义:一般地,将总体中的N个个体编号,并把号码分别写在号签上,再将号签放在一个容器中,搅拌均匀后,每次从中抽取一个号签,不放回的连续抽取 n 次,就得到一个容量为 n 的样本,这样的抽样方法就叫抽签法.
⑵随机数表法
例 要考察某种品牌的850颗种子的发芽率,从中抽取50颗种子作为样本进行试验.
方法:
①对850颗种子进行编号,可编为001,002,003,…,850;
②在面对随机数表(其中每个数都是随机方法产生的,这样的数表叫随机数表)之前,指出开始数字的纵横位置(例如从第1行第1列的数4开始);
③获取样本号码(给出的随机数表中是5个数一组,我们使用各个5位数组的前3位,不大于850且不与前面重复的取出,否则就跳过不取,如此下去直到得出50个三位数).
学生看书讨论回答问题
35′
教 与 学 互 动 设 计
教 师 活 动 内 容
学生活动内容
时间
随机数表法抽样的一般步骤:
①编号;
②在随机数表上确定起始位置;
③取数.
1.系统抽样的定义
情境一:了解某省农村家庭年平均收入情况.
情境二:检测某电视机厂生产的某种型号的电视机的质量是否合格.
定义:将总体分成均衡的若干部分,然后按照预先制定的规则,从每一部分抽取一个个体,得到所需要的样本,这种抽样叫做系统抽样(也称为等距抽样).
2.系统抽样的方法
例 为了解某地区近年高一学生期末考试数学成绩,拟从参加考试的15 000名学生的数学成绩中抽取容量为150的样本.
抽取方法:
⑴对全体学生进行编号,号码为1~15 000;
⑵k = EQ \F(N,n) = EQ \F(15000,150) =100 (即可以将总体平均分为150个部分,其中每一部分包含100个个体) ;
⑶从1号到100号进行简单随机抽样,抽取一个号码,比如是56.
⑷按照确定的规则,接下来顺次取出的号码为156,256, …,14 956的学生.
3.系统抽样的一般步骤
从元素个数为N总体中抽取容量为n的样本:
采用随机的方式将总体中的个体编号 (为简便起见,有时可直接采用个体所带有的号码,如考生的准考证号、街道上各户的门牌号,等等)
(2)将整个的编号分段(即分成若干部分),确定分段的间隔k = EQ \F(N,n) ;
25′
3′
2′
教 与 学 互 动 设 计
教 师 活 动 内 容
学生活动内容
时间
(3)在第一段用简单随机抽样确定起始的个体编号s;
(4)按照事先确定的规则抽取样本(通常是s,s+k,s+2k,s+3k,…,s+(n-1)k获取整个样本).
注意:当 EQ \F(N,n)是整数时,k= EQ \F(N,n);当 EQ \F(N,n)不是整数时,可随机地从总体中剔除余数,使剩下的总体中个体的数量N' 能被n整除,这时k = EQ \F(N',n) .然后再用系统抽样方法进行抽样.
练习
1.请从参加考试的15 000名学生的数学成绩中,抽取容量为100的样本.
2.某批产品共有1 563件,产品按出厂顺序编号,号码为1~1 563.检测员要从中抽取15件产品作检测,请你给出一个系统抽样方案.
情境一:某高中学生有900名.为了考察他们的体重状况,打算抽取容量为45的一个样本.已知高一有400名学生,高二有300名学生,高三有200名学生.
试问:能在900人中任意取45个吗?能将45个份额均匀分到这三部分中吗?应用什么方法抽取?
1.分层抽样的定义
当总体由差异明显的几部分组成时,为了使抽取的样本更好地反映总体的情况,常将总体中各个个体按照某种特征分成若干个互不重叠的部分,每一部分叫做“层”,在各层中按层在总体中所占的比例进行抽样,这种抽样叫做“分层抽样”.
情境一的抽样方法:
(1)确定样本容量与总体的个体数之比45 :900 = 1 :20;
(2)利用抽样比确定各年级应抽取的个体数,依次为 EQ \F(400,20), EQ \F(300,20), EQ \F(200,20),即20,15,10;
(3)利用简单随机抽样或系统抽样的方法,从各年级分别抽取20,15,10人,然后合在一起,就是所抽取的样本.
学生阅读分层抽样的概念.
教师对概念作强调说明:(1)分层需遵循不重复、不遗漏的原则;(2)抽取比例由每层个体占总体的比例确定;(3)各层抽样按简单随机抽样进行.
25′
3′
2′
教 与 学 互 动 设 计
教 师 活 动 内 容
学生活动内容
时间
2.分层抽样的一般步骤
分层抽样的一般步骤是:
(1)分层:按某种特征将总体分成若干层.
(2)按比例确定每层抽取个体的个数.
(3)各层分别按简单随机抽样的方法抽取.
(4)综合每层抽样,组成样本.
练习
某公司有员工 500 人,其中不到 35 岁的有125 人,35 到 49 岁的有 280 人,50 岁以上的有 95 人.为了调查员工的身体状况,从中抽取一个容量为 100 的样本,用分层抽样应当怎样抽取?
解 (1)确定样本容量与总体的个体数之比100 :500=1 :5;
(2)利用抽样比确定各年龄段应抽取的个体数,依次为 EQ \F(125,5), EQ \F(280,5), EQ \F(95,5),即25,56,19;
(3)利用简单随机抽样或系统抽样的方法,从各年龄段分别抽取25,56,19人,然后合在一起,就是所抽取的样本.
小结
填表:
类别
共同点
适用范围
步骤
简单随机抽样
系统抽样
分层抽样
作业教材P179练习A组第1,3题,B组题.
学生看书讨论回答问题
2′
3′
20′
语文版(中职)基础模块下册10.2 随机事件与概率教案及反思: 这是一份语文版(中职)基础模块下册10.2 随机事件与概率教案及反思,共6页。教案主要包含了复习引入,课堂活动,课堂检测等内容,欢迎下载使用。
语文版(中职)基础模块下册第七单元 数列7.1 数列的概念教学设计: 这是一份语文版(中职)基础模块下册第七单元 数列7.1 数列的概念教学设计,共5页。教案主要包含了学习目标,自主学习,合作探究,课堂总结,检测巩固等内容,欢迎下载使用。
语文版(中职)基础模块下册8.6 圆的方程教案: 这是一份语文版(中职)基础模块下册8.6 圆的方程教案,共4页。教案主要包含了圆的方程的建立等内容,欢迎下载使用。












