

高中数学湘教版(2019)必修 第一册3.1 函数综合训练题
展开绝密★启用前
3.1函数同步练习
湘教版(2019)高中数学必修第一册
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
一、单选题(本大题共12小题,共60.0分)
- 下列各组函数的图象相同的是
A.
B.
C.
D.
- 给出四个命题:
函数是其定义域到值域的映射;是函数;
函数的图象是一条直线;与是同一个函数.
其中正确的有
A. 个 B. 个 C. 个 D. 个
- 给出下列四个命题:
函数是定义域到值域的映射;
是函数;
函数的图象是一条直线;
与表示同一个函数.
其中正确的个数为
A. B. C. D.
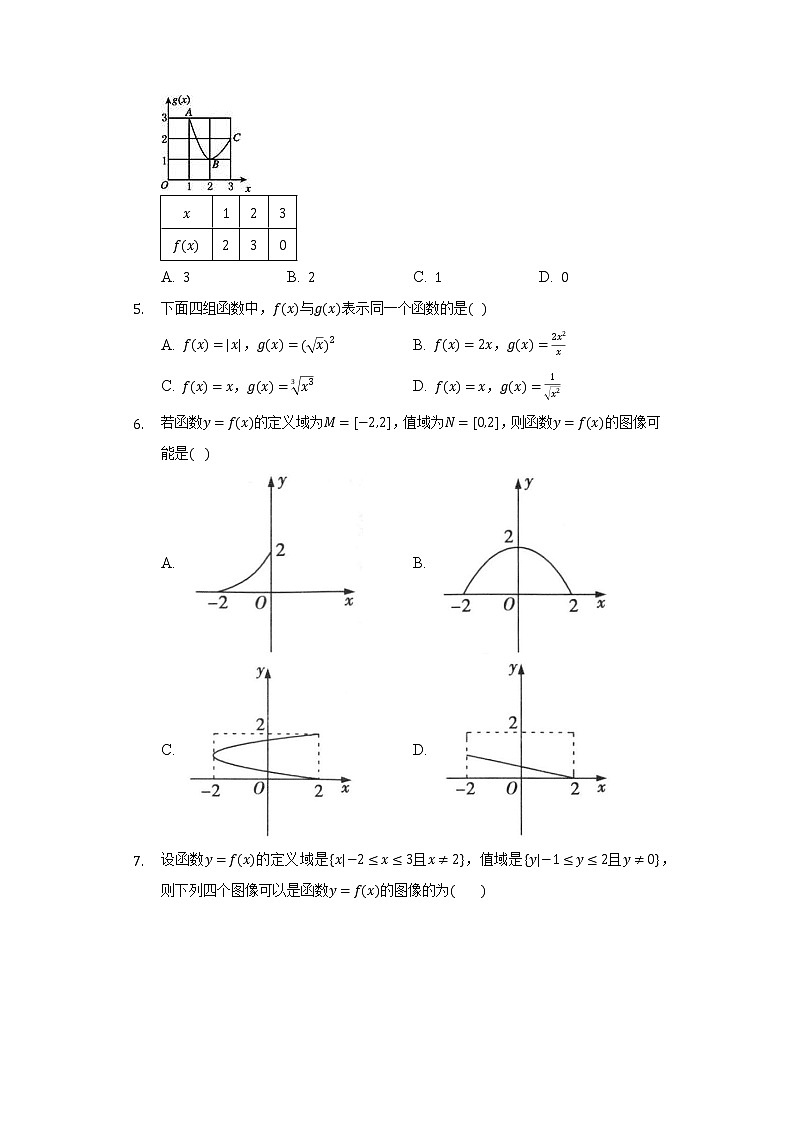
- 已知函数的对应关系如下表,函数的图像是如图所示的曲线,其中,,,则的值为
A. B. C. D.
- 下面四组函数中,与表示同一个函数的是
A. , B. ,
C. , D. ,
- 若函数的定义域为,值域为,则函数的图像可能是
A. B.
C. D.
- 设函数的定义域是且,值域是且,则下列四个图像可以是函数的图像的为
A. B.
C. D.
- 下列各组函数是同一函数的是
A. 与 B. 与
C. 与 D. 与
- 下列各组函数中,与表示同一函数的是
A. , B. ,
C. , D. ,
- 已知,,下列图形能表示以为定义域,为值域的函数的是
A. B.
C. D.
- 下列函数中,与函数是相等函数的是
A. B. C. D.
- 下列各组函数中,表示同一函数的是
A. 与
B. 与
C. 与
D. 与
二、多空题(本大题共5小题,共25.0分)
- 已知函数、分别由下表给出:
则的值为 ,满足的值是 . - 已知函数,分别由下表给出.
则 ; .
- 设表示不超过的最大整数,已知函数,则 ;其值域为 .
- 已知函数,分别由下表给出.
则 ; .
- 已知,分别是定义在上的偶函数和奇函数,且,则 , .
三、解答题(本大题共8小题,共96.0分)
- 已知函数.
求,的值
求证:是定值
求的值.
- 已知函数和,设.
求函数;
求和的值;
求的值;
若函数,试判断与是否为同一函数,并说明理由.
- 求下列函数的定义域、值域:
某种新药在试验药效时得到每毫升血液中含药量随时间变化的图像如图所示.从中发现,如果成人按规定剂量服用,服药后血液中的含药量最高,达到;接着逐步衰减,血液中的含药量为;
某个居民月份使用煤气情况如下表:
- 判断下列各组中两个函数是否为同一函数.
与;
与;
与.
- 已知二次函数的最小值为,且关于的不等式的解集为.求函数的解析式;
当时,求函数的值域.
- 已知函数.
求函数的定义域和值域
分别求,,.
- 已知函数是定义在上的偶函数,且当时,.
现已画出函数在轴左侧的图像,请补全函数的图像,并根据图像写出函数的单调递增区间;
写出函数的值域;
求出函数的解析式.
- 已知函数.
求函数的定义域;
求,的值.
答案和解析
1.【答案】
【解析】
【分析】
本题考查函数的概念,是基础题.
两个函数图象相同,则要求对应法则相同,定义域相同、值域相同,逐项判断即可得.
【解答】
解:对于,函数的定义域为,值域为,
而 的定义域为,值域为,故A不合题意;
对于,函数的定义域为,值域为,
而 ,则与的定义域、值域均相同,解析式相同,故B符合题意;
对于,函数的定义域为,但的定义域为,定义域不同,故
不合题意;
对于,两个函数的解析式不同,故D不合题意;
故选B.
2.【答案】
【解析】
【分析】
本题考查函数、映射及相等函数的概念、函数的图象,逐一判断即可.
【解答】
解:函数是其定义域到值域的映射,正确;
由,解得,所以,故不是函数;
函数的图象是离散的点,故不正确;
函数 与的定义域不同,不是同一函数,故不正确.
故选A.
3.【答案】
【解析】
【分析】
本题考查函数、映射及相等函数的概念、函数的图象,逐一判断即可.
本题考查了函数的定义及其性质,属于基础题.
【解答】
解:函数是其定义域到值域的映射,正确;
由,解得,所以定义域为空集,故不是函数;
函数的图象是离散的点,故不正确;
函数 与的定义域不同,不是同一函数,故不正确.
故选A.
4.【答案】
【解析】
【分析】
本题考查函数求值问题,涉及函数的基本概念,函数定义域与值域,函数的表示方法,属于基础题.
先根据函数的图象求出,再由函数的对应关系表求可得.
【解答】
解:由函数的图像过点,可知,
由表格可知,
所以.
故选B.
5.【答案】
【解析】
【分析】
本题考查了判断两函数是否为同一函数的方法,属于基础题.
由函数的定义域及对应关系是否相同分别判断四个选项得答案.
【解答】
解:函数的定义域为,的定义域为,定义域不同,不是同一函数;
函数的定义域为,的定义域为,定义域不同,不是同一函数;
,,定义域均为,对应法则也相同,两函数为同一函数;
的定义域为,的定义域为,定义域不同,不是同一函数.
故选C.
6.【答案】
【解析】
【分析】
本题考查函数的概念及图像,属于基础题.
解题时,根据函数的定义及定义域与值域,逐一判断即可求解
【解答】
解:选项A,定义域为,与条件不符,故A错误;
选项B,定义域、值域均与条件相符,故B正确;
选项C,不符合函数的定义,在内的任一的值,在内并非只有唯一的与之对应,故C错误;
选项D,值域与条件不符,故D错误.
综上所述,正确选项为.
故选:
7.【答案】
【解析】
【分析】
本题考查了函数的定义域和值域,函数图象,属于中档题.
根据函数的定义,结合图象逐一分析判断即可.
【解答】
解:观察发现,每一个图中都是一个对应一个,故都是函数图像.
对于,定义域是且,值域是,值域不满足
对于,定义域不满足
对于,定义域是且,值域是且,满足
对于,定义域不满足.
故选C.
8.【答案】
【解析】
【分析】
分别判断两个函数的定义域和对应法则是否一致,即可.
本题主要考查判断两个函数是否为同一函数,判断的主要标准是判断两个函数的定义域和对应法则是否一致,否则不是同一函数.
【解答】
解:定义域为,而定义域为且,两个函数的定义域不一样,所以不是同一函数.
B.与,两个函数的定义域和对应法则都一样,所以是同一函数.
C.与,两个函数的定义域和对应法则都不一样,所以不是同一函数.
D.与的对应法则不一致,所以不是同一函数.
故选B.
9.【答案】
【解析】
【分析】
本题考查函数概念,函数三要素,同一函数概念,属于基础题.
两函数是同一函数的条件是定义域和对应法则均相同即可.
【解答】
解:两函数的解析式不相同,所以不是同一函数,此选项错误;
B.的定义域是,的定义域为,定义域不同,不是同一函数,此选项错误;
C.与定义域均为,且解析式相同,是同一函数,此选项正确;
D.的定义域为,的定义域为,定义域不同,不是同一函数,此选项不正确.
故选C .
10.【答案】
【解析】
【分析】
本题考查函数的概念和定义域、值域,属于基础题.
由题意结合函数的概念逐个选项进行分析即可.
【解答】
解:是函数图象,其值域为,故不符合题意;
是函数的图象,定义域为,值域为,故符合题意;
是函数图象,值域为,故不符合题意;
是函数图象,值域为,故不符合题意.
故选B.
11.【答案】
【解析】
【分析】
本题考查判断两个函数是否为同一个函数的问题,解题时应判断它们的定义域,值域和对应关系是否相同,是基础题.
根据同一函数的概念对选项一一判断即可.
【解答】
解:对于,函数的定义域为
而函数的定义域为,不是同一个函数;
对于,,定义域也相同,是同一个函数;
对于,,与已知函数的定义域不同,不是同一个函数;
对于,,与已知函数对应关系不同,不是同一个函数.
故选.
12.【答案】
【解析】
【分析】
本题考查同一函数概念,属于基础题.
根据函数的定义域,解析式是否相同逐个检验即可.
【解答】
解: 的定义域为,的定义域为,定义域不同,不是同一函数, A错误
的定义域为,的定义域为,定义域不同,不是同一函数, B错误
C.定义域为,定义域, 定义域不同,不是同一函数, C错误
D. ,两个函数的定义域都是不等于的实数,定义域和解析式都相同,是同一函数,D正确.
故选D.
13.【答案】
【解析】
【分析】
本题主要考查函数的表格表示方法,及复合函数求值问题,属于基础题.
按照由内到外的原则计算,即可得到答案.
【解答】
解:因为,
又,
,
,
,
,
满足的值只有.
故答案为.
14.【答案】
【解析】
【分析】
本题考查函数的概念,列表表示函数的方法,根据表求函数值的方法.
由条件分别求出和,进而可求得结果.
【解答】
解:,所以;
,所以.
故答案为;.
15.【答案】
【解析】
【分析】
本题考查了新定义的函数的值域问题,解题时要充分理解的含义.
由是不超过的最大整数,代入可得答案,由的定义域是,分析出,从而得出值域.
【解答】
解:是不超过的最大整数,,
因为,
又因为函数的定义域是,
,
,
即的值域是;
故答案为.
16.【答案】
【解析】
【分析】
本题考查函数的表示方法,考查根据列表法求函数值,属于基础题.
由条件分别求出和,进而可求得结果.
【解答】
解:,所以;
,所以.
故答案为;.
17.【答案】
【解析】
【分析】
根据,的奇偶性即可得出,,从而得出,从而可求出,而联立即可解出.
本题考查奇函数和偶函数的定义,以及联立方程组求函数解析式的方法,属于基础题.
【解答】
解:,分别是定义在上的偶函数和奇函数;
,;
又;
,且;
联立解得.
故答案为:,.
18.【答案】解:函数,
,
.
因为,,
所以.
.
【解析】本题考查函数值的计算,函数解析式的化简,属于一般题.
直接代入计算,的值;
根据函数解析式,计算得到定值;
运用第问中结论计算即可得到答案.
19.【答案】解:.
的定义域为的定义域为
的定义域为与的定义城的交集,即.
;
,.
,不存在;
当时,即当时,;
当时,即当时,不存在;
和,虽然函数解析式相同,但是定义域不同,
前者定义域,后者定义域为.
和不是同一函数.
【解析】本题考查函数的基本概念,函数解析式的求解,函数的定义域,属于基础题.
由,即可求得函数;
先判断,是否在的定义域上,再进行求解;
对是否在的定义域上分类讨论,即可得解;
根据函数的定义,由和的定义域不同,即可判断两者不是同一函数.
20.【答案】解:根据图像,设以后的函数解析式为,
由题意知图像过点,
,解得,
,
由得,
函数的定义域为,值域为;
根据表格,得定义域为,值域为.
【解析】本题考查函数的定义域和值域、函数的解析式以及函数的表示方法,属于基础题.
先求出以后的函数解析式,再求出与轴的交点,即可求出结果;
利用表格直接求即可.
21.【答案】解:因为与的函数解析式,定义域和值域都相同,所以为同一函数
的定义域为,的定义域为,两函数的定义域不相同,所以不是同一函数
,,两函数的解析式不相同,所以不是同一函数.
【解析】本题考查函数的基本概念.
因为与的函数解析式,定义域和值域都相同,所以为同一函数
的定义域为,的定义域为,两函数的定义域不相同,所以不是同一函数
,,两函数的解析式不相同,所以不是同一函数.
22.【答案】解:设,
的解集为,
和为的两根,且,
,即
,
最小值为,是开口向上的抛物线,且对称轴为,
,
解得:,
由知,为开口向上,对称轴为的二次函数,
,
当时,;
当时,,
在上的值域为.
【解析】本题考查二次函数及一元二次不等式与相应函数和方程的关系,属于中档题.
设的解析式,由已知得,为方程的两根,从而得,,的关系,然后利用最小值为求解即可
利用二次函数求解即可.
23.【答案】解:函数的定义域为,
因为,
所以的值域为
,
,
.
【解析】本题主要考查函数的定义域、值域,考查函数值的求解,属于基础题.
使函数有意义的的取值范围就是定义域,利用配方法求值域即可;
分别把,,带入求解即可.
24.【答案】解:函数的图象补充完整后,图象如下图所示:
由图可得,递增区间为,;
结合函数的图象可得,
当或时,函数取得最小值为,
函数没有最大值,
故函数的值域为;
当时,,
再根据时,,
可得,
再根据函数为偶函数,
可得,
函数的解析式为.
【解析】本题考查函数图象的作法、函数解析式的确定与函数的单调性,考查了学生的计算能力,培养了学生分析问题与解决问题的能力.
根据偶函数的图象关于轴对称,可作出的图象,由图象可得的单调递增区间;
结合函数的图象可得值域.
令,则,根据条件可得,利用函数是定义在上的偶函数,可得,从而可得函数的解析式.
25.【答案】解:使根式有意义的实数的集合是,
使分式有意义的实数的集合是,
所以这个函数的定义域是且;
,.
【解析】本题考查函数的定义域,函数的求值,属于基础题.
分别列出使与有意义的不等式,解不等式组即可;
分别令和代入解析式即可得函数值.
湘教版(2019)必修 第一册3.1 函数课后作业题: 这是一份湘教版(2019)必修 第一册3.1 函数课后作业题,共26页。试卷主要包含了0分),2]=1,[−2,【答案】C,【答案】B,【答案】ACD,【答案】AD等内容,欢迎下载使用。
高中数学湘教版(2019)必修 第一册4.4 函数与方程课后测评: 这是一份高中数学湘教版(2019)必修 第一册4.4 函数与方程课后测评,共27页。试卷主要包含了4函数与方程同步练习,0分),25)B,【答案】C,【答案】B等内容,欢迎下载使用。
高中数学湘教版(2019)必修 第一册4.3 对数函数课后复习题: 这是一份高中数学湘教版(2019)必修 第一册4.3 对数函数课后复习题,共22页。试卷主要包含了3对数函数同步练习,0分),6,lg25≈2,【答案】B,【答案】C,【答案】A,【答案】D等内容,欢迎下载使用。













