



专题43抛物线-2022年(新高考)数学高频考点+重点题型学案
展开专题43抛物线--2022年(新高考)数学高频考点+重点题型
知识点一 抛物线的定义
平面内与一个定点F和一条定直线l(l不经过点F)距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
知识点二 抛物线的标准方程与几何性质
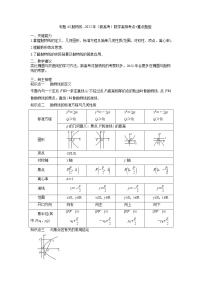
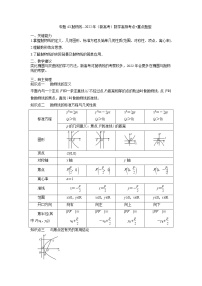
标准方程 | y2=2px (p>0) | y2=-2px (p>0) | x2=2py (p>0) | x2=-2py (p>0) |
p的几何意义:焦点F到准线l的距离 | ||||
图形 | ||||
顶点 | O(0,0) | |||
对称轴 | x轴 | y轴 | ||
焦点 | F | F | F | F |
离心率 | e=1 | |||
准线 | x=- | x= | y=- | y= |
范围 | x≥0,y∈R | x≤0,y∈R | y≥0,x∈R | y≤0,x∈R |
开口方向 | 向右 | 向左 | 向上 | 向下 |
焦半径(其中P(x0,y0)) | = x0+ | = -x0+ | = y0+ | = -y0+ |
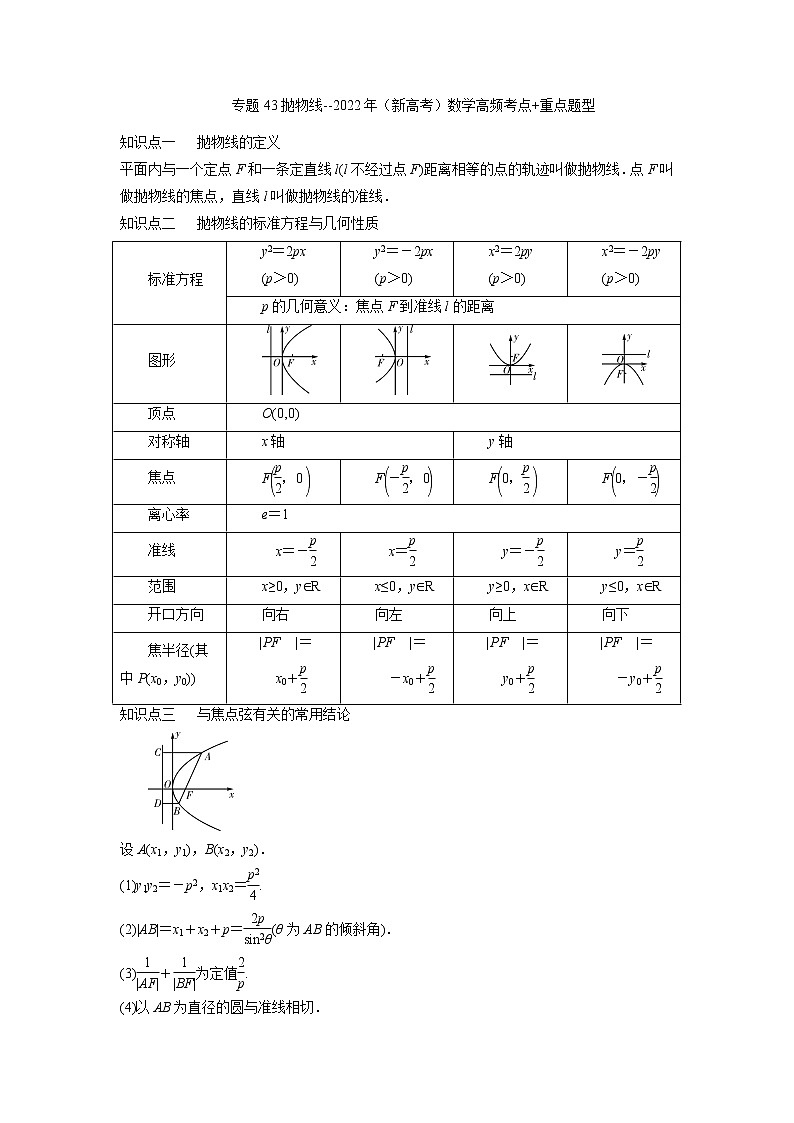
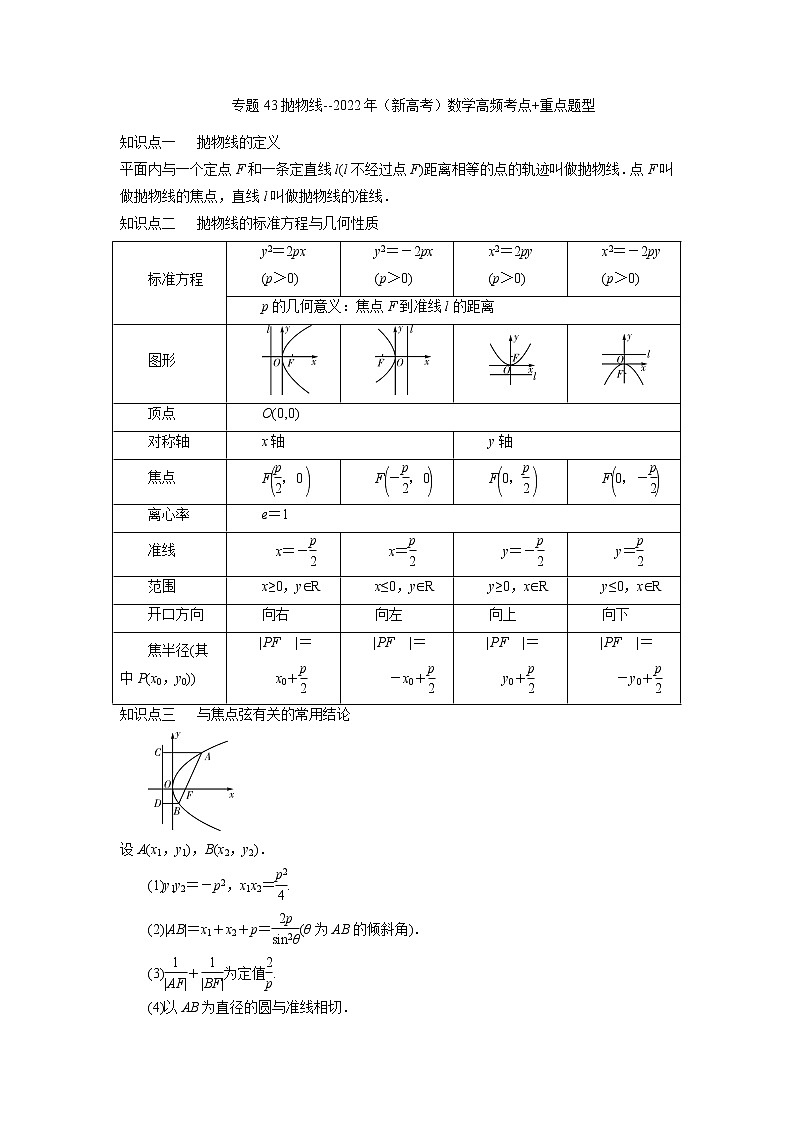
知识点三 与焦点弦有关的常用结论
设A(x1,y1),B(x2,y2).
(1)y1y2=-p2,x1x2=.
(2)|AB|=x1+x2+p=(θ为AB的倾斜角).
(3)+为定值.
(4)以AB为直径的圆与准线相切.
(5)以AF或BF为直径的圆与y轴相切.
【知识必备】
设AB是过抛物线y2=2px(p>0)焦点F的弦,若A(x1,y1),B(x2,y2),则
(1)x1x2=,y1y2=-p2;
(2)|AF|=,|BF|=,弦长|AB|=x1+x2+p=(α为弦AB的倾斜角);
(3)+=;
(4)以弦AB为直径的圆与准线相切;
(5)以AF或BF为直径的圆与y轴相切;
(6)过焦点弦的端点的切线互相垂直且交点在准线上.
四、高频考点+重点题型
考点一.双曲线的定义及其应用
1.(2020·新课标Ⅰ)已知A为抛物线C:y2=2px(p>0)上一点,点A到C的焦点的距离为12,到y轴的距离为9,则p=( )
A. 2 B. 3 C. 6 D. 9
2.(2017· 全国卷Ⅱ)已知F是抛物线C:y2=8x的焦点,M是C上一点,FM的延长线交y轴于点N.若M为FN的中点,则|FN|=________.
3.若抛物线y2=4x上一点P到其焦点F的距离为2,O为坐标原点,则△OFP的面积为( )
A. B.1 C. D.2
4.设P是抛物线y2=4x上的一个动点,F是抛物线的焦点.若B(3,2),则|PB|+|PF|的最小值为________.
5.抛物线y2=8x的焦点为F,点A(6,3),P为抛物线上一点,且P不在直线AF上,则△PAF周长的最小值为______.
6.已知F是抛物线y2=x的焦点,A、B是该抛物线上的两点,AF+BF=3,则线段AB的中点到y轴的距离为__________.
7.(2019·襄阳测试)已知抛物线y=x2的焦点为F,准线为l,M在l上,线段MF与抛物线交于N点,若|MN|=|NF|,则|MF|=________.
8.如图,点F是抛物线y2=8x的焦点,点A,B分别在抛物线y2=8x及圆(x-2)2+y2=16的实线部分上运动,且AB始终平行于x轴,则△ABF的周长的取值范围是________.
考点二.抛物线的标准方程及其几何性质
1.(2020·新课标Ⅲ)设O为坐标原点,直线x=2与抛物线C:y2=2px(p>0)交于D,E两点,若OD⊥OE,则C的焦点坐标为( )
A. (,0) B. (,0) C. (1,0) D. (2,0)
2.【2019·全国Ⅱ卷】若抛物线y2=2px(p>0)的焦点是椭圆的一个焦点,则p=
A.2 B.3
C.4 D.8
3.(2021·衡水中学调研)若抛物线y2=2px(p>0)上一点到焦点和到抛物线对称轴的距离分别为10和6,则抛物线的方程为( )
A.y2=4x B.y2=36x C.y2=4x或y2=36x D.y2=8x或y2=32x
4.如图所示,过抛物线y2=2px(p>0)的焦点F的直线依次交拋物线及准线于点A,B,C,若|BC|=2|BF|,且|AF|=4,则拋物线的方程为( )
A.y2=8x B.y2=4x C.x2=2x D.y2=x
5.设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点A(0,2),则C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x
6.如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A,B,交其准线于点C,若|BC|=2|BF|,且|AF|=6,则此抛物线方程为( )
A.y2=9x B.y2=6x
C.y2=3x D.y2=x
7.已知抛物线x2=2py(p>0)的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,若△FPM为边长是4的等边三角形,则此抛物线的方程为________.
考点三、焦点弦探究
1.(2020·山东卷)斜率为的直线过抛物线C:y2=4x的焦点,且与C交于A,B两点,则=________.
2.已知抛物线C的顶点是原点O,焦点F在x轴的正半轴上,经过F的直线与抛物线C交于A,B两点,如果•12,那么抛物线C的方程为( )
A.x2=8y B.x2=4y C.y2=8x D.y2=4x
3.已知直线y=k(x+2)(k>0)与抛物线C:y2=8x相交于A、B两点,F为C的焦点,若|FA|=2|FB|,则k=( )
A. B. C. D.
4.(2020•青岛模拟)过抛物线y2=2px(p>0)的焦点F作倾斜角为60°的直线l交抛物线于A,B两点,且|AF|>|BF|,则的值为( )
A.3 B.2 C. D.
5.已知直线l:x﹣y﹣m=0经过抛物线C:y2=2px(p>0)的焦点,l与C交于 A、B两点.若|AB|=6,则p的值为( )
A. B. C.1 D.2
6.已知抛物线C:y2=4x的焦点为F,过点F分别作两条直线l1,l2,直线l1与抛物线C交于A、B两点,直线l2与抛物线C交于D、E两点,若l1与l2的斜率的平方和为1,则|AB|+|DE|的最小值为( )
A.16 B.20 C.24 D.32
考点四、非焦点弦探究
1.(2019·全国卷Ⅰ)已知抛物线C:y2=3x的焦点为F,斜率为的直线l与C的交点为A,B,与x轴的交点为P.
①若|AF|+|BF|=4,求l的方程;
②若=3,求|AB|.
2.(2018·全国卷Ⅰ)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点.
(1)当l与x轴垂直时,求直线BM的方程;
(2)证明:∠ABM=∠ABN.
考点五.抛物线中的范围与最值问题
1.设P是抛物线y2=4x上的一个动点,则点P到点A(-1,1)的距离与点P到直线x=-1的距离之和的最小值为________.
2.(2020·广东省珠海模拟)已知抛物线y2=4x,过点P(4,0)的直线与抛物线相交于A(x1,y1),B(x2,y2)两点,则y+y的最小值为( )
A.12 B.24 C.16 D.32
3.已知抛物线E:y2=2px(p>0)的焦点为F,过点F且倾斜角为的直线l被E截得的线段长为8.
(1)求抛物线E的方程;
(2)已知点C是抛物线上的动点,以C为圆心的圆过点F,且圆C与直线x=-相交于A,B两点. 求FA·FB的取值范围.
4.(2021春•孝南区校级月考)已知曲线M上任意一点P到点F(0,2)的距离比到x轴的距离大2,直线l:y=kx+2与曲线M交于A,D两点,与圆N:x2+y2﹣4y+3=0交于B,C两点(A,B在第一象限),则|AC|+4|BD|的最小值为 .
考点六 直线与抛物线的位置关系
1.设A,B为曲线C:y=上两点,A与B的横坐标之和为2.
(1)求直线AB的斜率;
(2)设M为曲线C上一点,曲线C在点M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.
达标测试
一、单项选择题
1.(2021·山东菏泽模拟)过抛物线C:x2=2y的焦点F的直线l交抛物线C于A,B两点,若抛物线C在点B处的切线斜率为1,则|AF|=( )
A.1 B.2 C.3 D.4
2. 抛物线y2=x上一点P到焦点的距离是2,则P点坐标为( )
A. B. C. D.
3. 已知点A(-2,3)在抛物线C:y2=2px的准线上,记C的焦点为F,则直线AF的斜率为( )
A. B. C. D.
4.(2021·模拟)已知F是抛物线C1:y2=2px(p>0)的焦点,曲线C2是以F为圆心,为半径的圆,直线4x-3y-2p=0与曲线C1,C2从上到下依次相交于点A,B,C,D,则=( )
A.16 B.4 C. D.
5. 圆心在第一象限,且半径为1的圆与抛物线y2=2x的准线和双曲线-=1的渐近线都相切,则圆心的坐标是( )
A. B. C.或 D.
6.直线4kx-4y-k=0与拋物线y2=x交于A、B两点,若|AB|=4,则弦AB的中点到直线x+=0的距离等于( )
A. B. C. D.
二、多项选择题
7.已知抛物线C:的焦点为F,其准线l与x轴交于点P,过C上一点M作l的垂线,垂足为Q,若四边形MQPF为矩形,则( )
A. 准线l的方程为 B. 矩形MQPF为正方形
C. 点M的坐标为 D. 点M到原点O的距离为
8.已知抛物线与双曲线有相同的焦点,点在抛物线上,则下列结论正确的有
A. 双曲线的离心率为2 B. 双曲线的渐近线为
C. D. 点P到抛物线的焦点的距离为4
三、填空题
9. 直线y=x-3与抛物线y2=4x交于A、B两点,过A、B两点向抛物线的准线作垂线,垂足分别为P、Q,则梯形APQB的面积为________.
10.(2021·山东省滨州模拟)已知抛物线x2=2py(p>0)的焦点为F,点P为抛物线上的动点,点M为其准线上的动点,若△FPM为边长是4的等边三角形,则此抛物线的方程为________.
11.在直角坐标系xOy中,直线l过抛物线y2=4x的焦点F,且与该抛物线相交于A、B两点,其中点A在x轴上方.若直线l的倾斜角为60°,则△OAF的面积为________.
12.已知拋物线C:y2=4x的焦点为F,准线为l,过拋物线C上的点A作准线l的垂线,垂足为M,若△AMF与△AOF(其中O为坐标原点)的面积之比为3∶1,则点A的坐标为________.
四、解答题
13.抛物线的焦点F是圆x2+y2-4x=0的圆心.
(1) 求该抛物线的标准方程;
(2) 直线l的斜率为2,且过抛物线的焦点,若l与抛物线、圆依次交于A、B、C、D,
求|AB|+|CD|.
14.(2021·广东省韶关模拟)设A,B为曲线C:y=上两点,A与B的横坐标之和为4.
(1)求直线AB的斜率;
(2)设M为曲线C上一点,C在M处的切线与直线AB平行,且AM⊥BM,求直线AB的方程.
专题42双曲线-2022年(新高考)数学高频考点+重点题型学案: 这是一份专题42双曲线-2022年(新高考)数学高频考点+重点题型学案,文件包含专题42双曲线--2022年新高考数学高频考点+重点题型原卷版docx、专题42双曲线--2022年新高考数学高频考点+重点题型解析版docx等2份学案配套教学资源,其中学案共37页, 欢迎下载使用。
专题11函数图像--2022年(新高考)数学高频考点+重点题型(解析版)学案: 这是一份专题11函数图像--2022年(新高考)数学高频考点+重点题型(解析版)学案,共23页。学案主要包含了关键能力,教学建议,自主梳理,高频考点+重点题型,利用图像研究函数性质等内容,欢迎下载使用。
专题41椭圆--2022年(新高考)数学高频考点+重点题型(解析版)学案: 这是一份专题41椭圆--2022年(新高考)数学高频考点+重点题型(解析版)学案,共21页。学案主要包含了关键能力,教学建议,自主梳理,高频考点+重点题型,焦点三角形等内容,欢迎下载使用。