2022届高考一轮复习第五章三角函数专练_三角函数大题（Word含答案解析）

这是一份2022届高考一轮复习第五章三角函数专练_三角函数大题（Word含答案解析），文件包含2022届高考一轮复习第五章三角函数专练_三角函数大题专练1含答案doc、2022届高考一轮复习第五章三角函数专练_三角函数大题专练2含答案doc、2022届高考一轮复习第五章三角函数专练_三角函数大题专练3含答案doc、2022届高考一轮复习第五章三角函数专练_三角函数大题专练4含答案doc等4份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
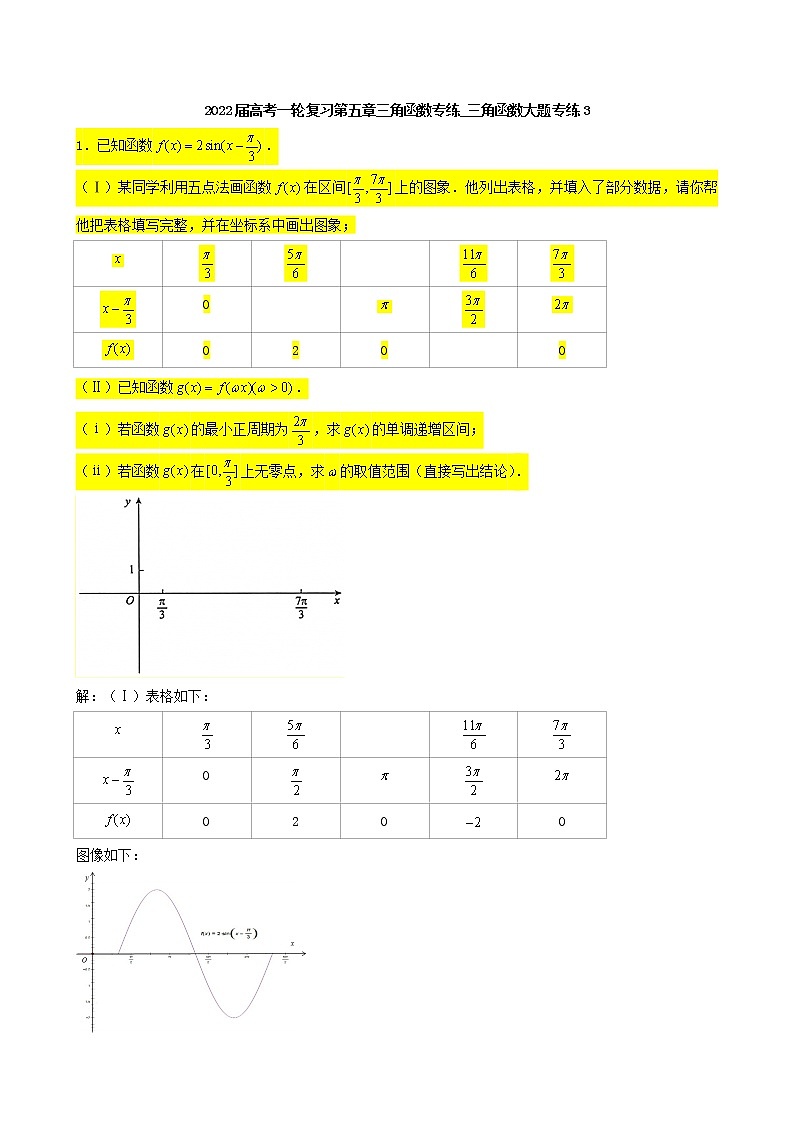
（Ⅰ）某同学利用五点法画函数在区间上的图象．他列出表格，并填入了部分数据，请你帮他把表格填写完整，并在坐标系中画出图象；
（Ⅱ）已知函数．
（ⅰ）若函数的最小正周期为，求的单调递增区间；
（ⅱ）若函数在上无零点，求的取值范围（直接写出结论）．
解：（Ⅰ）表格如下：
图像如下：
（Ⅱ）已知函数．
（ⅰ），．
，
函数的最小正周期为，解得，
，
令，，解得，，
可得的单调递增区间为，，；
（ⅱ）在上无零点，且，
，解得，
又，
，
又，即，可得，，解得，，
，
综上的取值范围为，，．
2．已知函数的最小正周期为．
（1）求的值；
（2）将图象上所有的点向右平移个单位长度，得到函数的图象，求的解析式；
（3）在（2）的条件下，若对于任意的，，当时，恒成立，求的取值范围．
解：（1），
因为函数的最小正周期为，所以，解得，所以的值为1．
（2）因为图象上所有的点向右平移个单位长度，得到函数的图象又，
所以，，
所以，的解析式为．
（3）令，
因为对于任意的，，当时，恒成立，
所以，在严格单调递增，
由，，
整理可得，，
所以，，严格单调递增去区间是，，
所以，，解得，
所以，的取值范围是．
3．已知函数其中为常数，，若，对任意恒成立，且．
（1）求的值；
（2）若不等式，在上恒成立，求实数的取值范围．
解：（1）函数其中为常数，，若，
所以，
即，
解得或，
由于，
故，
故，
故．
由于，，
故．
（2）由（1）得：，
由于，所以，
故．
由于在上恒成立，
故
整理得．
4．已知．
（1）求的单调区间；
（2）已知，对总存在，，使得成立，求的取值范围．
解：（1），
令，，
，，
的单调递减区间为，，，
令，，
，，
的单调递增区间为，，，
（2）由题意得，值域值域，
，，，，，，，，
，，，
①当时，，，
，，
②当时，（1），，
，，
③当时，（1），，
，不等式组无解，
综上，的取值范围为，．
5．已知函数．
（1）求的最小正周期及在区间上的最大值
（2）在锐角中，，且，求取值范围．
解：（1）函数．
所以函数的最小正周期为．
当，
所以，
当时，函数的最大值为．
（2）由于在锐角中，，
所以，解得．
利用正弦定理，
所以，，
由于，
所以．
所以，
由于，
所以，
故，
故．
即的取值范围为，．
6．已知函数．
（1）当时，求的单调递增区间；
（2）当，时，的值域为，，求、的值．
解：（1）时，，
，，
，；
所以的单调递增区间为，，；
（2），
当，时，，；
当时，由，解得；
当时，由，解得；
综上知，，；或，．
0
0
2
0
0
0
0
2
0
0