2022届高考一轮复习第六章解三角形专练_取值范围最值问题（Word含答案）

这是一份2022届高考一轮复习第六章解三角形专练_取值范围最值问题（Word含答案），文件包含2022届高考一轮复习第六章解三角形专练_取值范围最值问题1大题含答案doc、2022届高考一轮复习第六章解三角形专练_取值范围最值问题2大题含答案doc等2份试卷配套教学资源，其中试卷共12页， 欢迎下载使用。
这三个条件中任选一个，补充到下面的问题中并作答．
问题：在中，角，，的对边分别为，，，且 ____．
（1）求角；
（2）若，求的取值范围．
解：若选①：（1），
则，
，
，，
，，．
（2）由正弦定理得，
，，
则
，
，，，，，
，即的取值范围为．
若选②：，
由正弦定理得，，
，，．
下面步骤同①．
若选③：，
则，
由正弦定理得，，
，，．
下面步骤同①．
2．在锐角中，角，，的对边分别为，，，且．．
（Ⅰ）求角的大小；
（Ⅱ）当时，求的取值范围．
解：（Ⅰ）由，
得，
化简，
由于为锐角三角形，所以，得，
又，
故，
（Ⅱ）由正弦定理得，
得，
又，
所以，，
所以
故，
由余弦定理得，
所以．
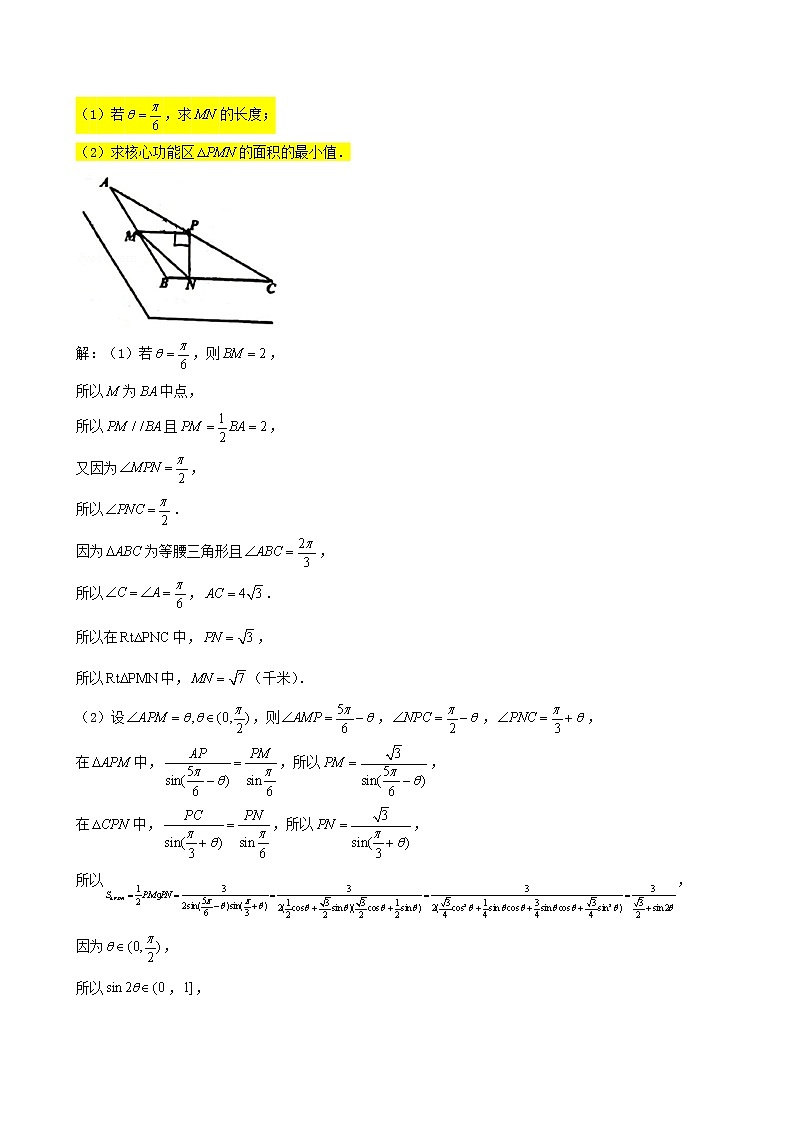
3．某规划部门拟在一条河道附近建设一个如图所示的“创新产业园区”．已知整个可用建筑用地可抽象为，其中折线为河岸，经测量河岸拐弯处，千米，且为等腰三角形．根据实际情况需要在该产业园区内再规划一个核心功能区，其中、分别在、（不包括端点）上，为中点，且，设．
（1）若，求的长度；
（2）求核心功能区的面积的最小值．
解：（1）若，则，
所以为中点，
所以且，
又因为，
所以．
因为为等腰三角形且，
所以，．
所以在中，，
所以中，（千米）．
（2）设，则，，，
在中，，所以，
在中，，所以，
所以，
因为，
所以，，
所以时，的面积的最小值为．
4．在中，内角，，所对的边分别为，，，已知，．
（1）求角的大小；
（2）若是锐角三角形，求的取值范围．
解：（1）由及正弦定理得，得，，
因为，
所以，
所以，即，
由余弦定理得，
由为三角形内角得；
（2）由（1）知，
，
，
，
，
，
由题意可知且，
解得，
所以，
所以，
所以，
故求的取值范围，．
5．已知的三个内角，，对应的边分别为，，，．
（1）求角的大小；
（2）如图，设为内一点，，，且，求的最大值．
解（1）．
．
．
整理得．
易知，，
又为三角形内角，
．
（2）由（1）与，得，
在中，由余弦定理，，
又在中，，
，当且仅当时取等“”所以的最大值为．
6．已知中，内角，，的对边分别为，，，，．
（1）求；
（2）若点与点在两侧，且满足，，求四边形面积的最大值．
解：（1）由以及正弦定理可知，
，
即．
，，
，．
，
，可得，可得．
（2）设，由余弦定理，可得，
可得四边形的面积
，（其中，
故四边形面积的最大值为．