江苏省无锡市华庄中学2021-2022学年八年级上学期期中考试数学【试卷+答案】

这是一份江苏省无锡市华庄中学2021-2022学年八年级上学期期中考试数学【试卷+答案】，共11页。试卷主要包含了11， 2等内容，欢迎下载使用。
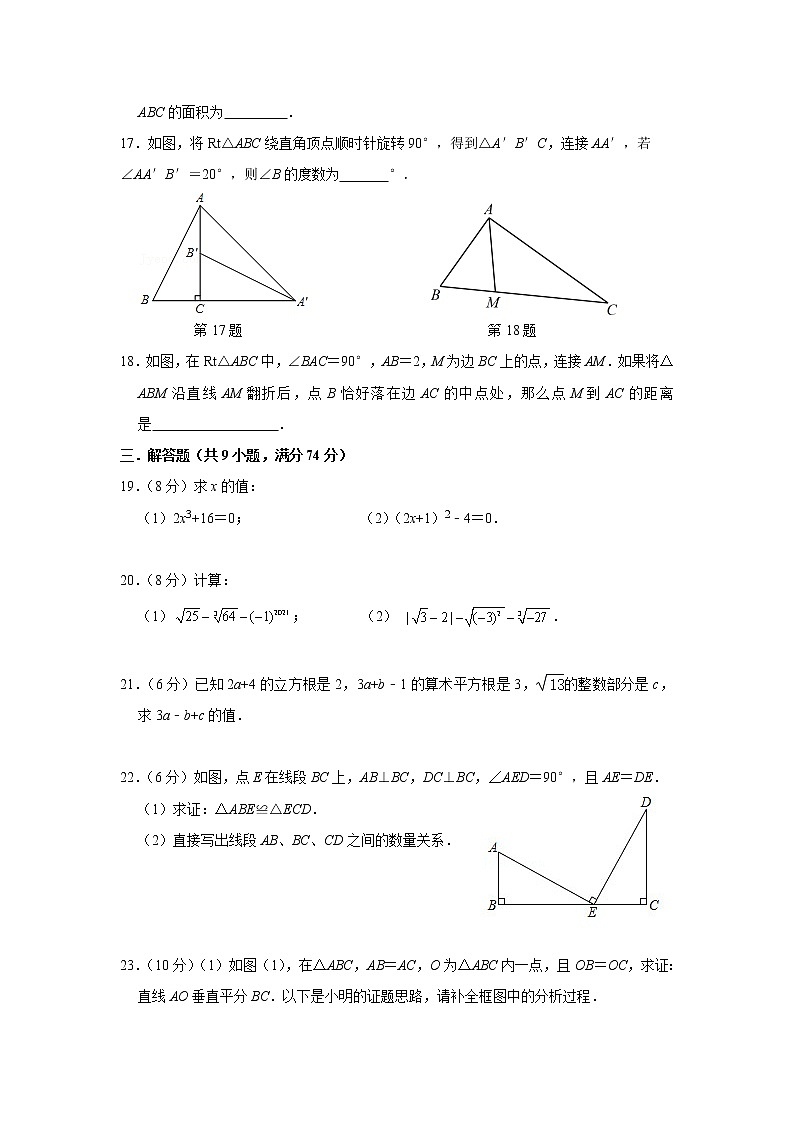
无锡市华庄中学2021秋学期期中考试试卷         初二数学            2021.11命题人：                  审卷人：       注意事项及说明：本卷分试题和答卷两部分，所有答案一律写在答卷上。本学科考试时间为100分钟，满分120分。一．选择题（共10小题，满分30分，每小题3分）1．下列图形：①两个点；②线段；③角；④长方形；⑤三角形，其中一定是轴对称图形的有（　　）A．2个 B．3个 C．4个 D．5个2．下列四个数中无理数是（　　）A． B． C． D．3．下列关于的说法中，错误的是（　　）A．是无理数 B．10的平方根是C． D．是10的算术平方根4．如图，AD、BC相交于点E．若△ABE≌△DCE，则下列结论中不正确的是（　　）A．∠A＝∠C B．AB∥CD C．E为BC中点 D．AB＝DC5．已知，则a的取值范围是（　　）A．a≤0 B．a＜0 C．0＜a≤1 D．a＞06．已知等腰三角形的周长为29，其中一边长为7，则该等腰三角形的底边长为（　　）A．11 B．7 C．15 D．15或77．如图，某同学把一块三角形的玻璃打破成了三块，现要到玻璃店去配一块大小、形状完全相同的玻璃，那么他可以（　　）A．带①去 B．带②去 C．带③去 D．带①和②去8．将一张宽为4cm的长方形纸片（足够长）折叠成如图所示图形，重叠部分是一个三角形，则这个三角形面积的最小值是（　　） A． cm2   B． 16cm2   C．cm2    D．8cm29．如图，△ABC中，E，F分别在AB，AC上，DE⊥DF，D是边BC的中点，则BE+CF（　　）A．大于EF B．等于EF C．小于EF D．与EF的大小关系不能确定10．如图，已知△ABC是等边三角形，点D、E在AB上，将△ACD、△BCE分别沿CD、CE翻折，点A、B分别落在点A′、B′的位置，再将△A′CD、△B′CE分别沿A′C、B′C翻折，点D与点E恰好重合于点O，则∠A′OB′的度数是（　　）A．120°  B．135°  C．140°  D．150°二．填空题（共8小题，满分16分，每小题2分）11．﹣27的立方根是 　   　．12．有理数205510，精确到万位，用科学记数法表示成的近似数是　        　．13．在镜子中看到时钟显示的时间          ，则实际时间是 　           　．14．已知：如图，∠CAB＝∠DBA，只需补充条件　      　，就可以根据“SAS”得到△ABC≌△BAD．                   第14题                                第15题15．如图，在△ABC中，∠C＝27°，∠ABC的平分线BD交AC于点D，如果DE垂直平分BC，那么∠A＝　   　°．16．若△ABC的周长为12，∠A和∠B的平分线相交于点P，点P到边AB的距离为1，则△ABC的面积为　     　．17．如图，将Rt△ABC绕直角顶点顺时针旋转90°，得到△A′B′C，连接AA′，若∠AA′B′＝20°，则∠B的度数为　   　°．                 
        第17题                                   第18题   18．如图，在Rt△ABC中，∠BAC＝90°，AB＝2，M为边BC上的点，连接AM．如果将△ABM沿直线AM翻折后，点B恰好落在边AC的中点处，那么点M到AC的距离是　              　．三．解答题（共9小题，满分74分）19．（8分）求x的值：（1）2x3+16＝0；                （2）（2x+1）2﹣4＝0． 20．（8分）计算：（1）；        （2） ． 21．（6分）已知2a+4的立方根是2，3a+b﹣1的算术平方根是3，的整数部分是c，求3a﹣b+c的值． 22．（6分）如图，点E在线段BC上，AB⊥BC，DC⊥BC，∠AED＝90°，且AE＝DE．（1）求证：△ABE≌△ECD．（2）直接写出线段AB、BC、CD之间的数量关系．   23．（10分）（1）如图（1），在△ABC，AB＝AC，O为△ABC内一点，且OB＝OC，求证：直线AO垂直平分BC．以下是小明的证题思路，请补全框图中的分析过程．  （2）如图（2），在△ABC中，AB＝AC，点D、E分别在AB、AC上，且BD＝CE．请你只用无刻度的直尺画出BC边的垂直平分线（不写画法，保留画图痕迹）．（3）如图（3），在五边形ABCDE中，AB＝AE，BC＝DE，∠B＝∠E，请你只用无刻度的直尺画出CD边的垂直平分线（不写画法，保留画图痕迹），并证明． 24．（8分）如图，在△ABC中，点D在AB上，且CD＝CB，E为BD的中点，F为AC的中点，连接EF交CD于点M，连接AM．（1）求证：（2）若EF⊥AC，求证：AM+DM＝CB．25．（10分）如图，△ABC中，点D在BC边上，∠BAD＝100°，∠ABC的平分线交AC于点E，过点E作EF⊥AB，垂足为F，且∠AEF＝50°，连接DE．（1）求∠CAD的度数；（2）求证：DE平分∠ADC；（3）若AB＝7，AD＝4，CD＝8，且S△ACD＝15，求△ABE的面积． 26．（8分）阅读理解：如图1，在△ABC的边AB上取一点P，连接CP，可以把△ABC分成两个三角形，如果这两个三角形都是等腰三角形，我们称点P是△ABC的边AB上的完美点．解决问题：（1）如图2，△ABC中，∠ACB＝90°，试找出边AB上的完美点P，并说明理由．（2）如图3，已知∠A＝36°，△ABC的顶点B在射线l上，点P是边AB上的完美点，请认真分析所有符合要求的点B，直接写出相应的∠B的度数．   27．（10分）在△ABC中，∠BAC＝90°，AB＝AC，∠ABC＝∠ACB＝45°，在△ABC外侧作∠ACM，使得∠ACM＝∠ABC，点D是射线CB上的动点，过点D作直线CM的垂线，垂足为E，交直线AC于F．（1）当点D与点B重合时，如图1所示，线段DF与EC的数量关系是什么？并说明理由；（2）当点D运动到CB延长线上某一点时，线段DF和EC是否保持上述数量关系？请在图2中画出图形，并说明理由．
  初二数学期中试卷参考答案   2021.11一、选择题（本大题共10小题，每小题3分，共30分．）1-10．CDBAC BCDAC   二、填空题（本大题共8小题，每空2分，共16分）11．﹣3    12. 2.1×105   13．21：05     14．AC＝BD 15．99     16．6        17．65         18． 三、解答题（本大题共有8小题，共74分）
19．（本题满分8分）解：（1）2x3+16＝0，          （2）（2x+1）2﹣4＝0，2x3＝﹣16，             （2x+1）2＝4，x3＝﹣8，                2x+1＝±2，x＝﹣2；                2x+1＝2  或  2x+1＝﹣2，…………4’        x1＝， x2＝﹣．    …………4’（只有1个答案2分）              20．（本题满分8分）计算：（1）原式  …………2’                （2）原式…………2’ ；         …………4’                 ． …………4’  21.（本题满分6分）解：∵2a+4的立方根是2，3a+b﹣1的算术平方根是3，∴2a+4＝8，3a+b﹣1＝9，   …………2’∴a＝2，b＝4，             …………4’∵c是的整数部分，∴c＝3，                  …………5’∴3a﹣b+c＝3×2﹣4+3＝5．  …………6’ 22．（本题满分6分）证明：（1）∵AB⊥BC，DC⊥BC，∴∠B＝∠C＝∠AED＝90°，∴∠A+∠AEB＝90°，∠AEB+∠DEC＝90°，∴∠A＝∠DEC，在△ABE和△ECD中∴△ABE≌△ECD（AAS）；                …………4’（2）∵△ABE≌△ECD∴CE＝AB，BE＝CD，∴BC＝BE+CE＝AB+CD．                 …………6’23．（本题满分10分）解：（1）AB＝AC，OB＝OC         ………2’（2）………4’      ………6’                                           （AC、AD可不连）证明略  ………10’24. （本题满分8分）（1）证明：连接CE，如图， ∵CD＝CB，E为BD的中点，∴CE⊥BD， ∵F为AC的中点，∴；………4’ （2）证明：∵EF⊥AC，F为AC的中点∴EF为AC中垂线∴AM＝CM，          ∵CD＝DM+MC，∴CD＝DM+AM，∵BC＝DC，∴AM+DM＝CB．       ………8’（其他证法，酌情给分）25. （本题满分10分）（1）解：∵EF⊥AB，∠AEF＝50°，∴∠FAE＝90°﹣50°＝40°，∵∠BAD＝100°，∴∠CAD＝180°﹣100°﹣40°＝40°；………3’（2）证明：过点E作EG⊥AD于G，EH⊥BC于H，∵∠FAE＝∠DAE＝40°，EF⊥BF，EG⊥AD，∴EF＝EG，∵BE平分∠ABC，EF⊥BF，EH⊥BC，∴EF＝EH，∴EG＝EH，∵EG⊥AD，EH⊥BC，∴DE平分∠ADC；………6’（3）解：∵S△ACD＝15，∴×AD×EG+×CD×EH＝15，即×4×EG+×8×EG＝15，解得，EG＝EH＝，∴EF＝EH＝，∴△ABE的面积＝×AB×EF＝×7×＝．………10’26. （本题满分8分）解：（1）取AB的中点P，连接PC即可如图①………1’∵∠ACB＝90°，P是AB的中点，∴CP＝AB，AP＝BP＝AB，∴AP＝PB＝CP．∴△APC，△PBC是等腰三角形．………3’∴点P是边AB上的完美点.………4’（2）满足条件的点B如图所示：②③④⑤⑥  ∠B=18o、36o、54o、72o        ………8’   （1种情况1分，全部答对得5分）27. （本题满分10分）（1）DF＝2EC： ………1’ 证明略  ………4（2）仍然成立，DF＝2EC； ………5’ 法一：作∠PDE＝22.5，交CE的延长线于P点，交CA的延长线于N。法二：过点D作交CE的延长线于点P，交CA的延长线于N。作图    ………7                                证明略      ………10’