人教版八年级上册13.3.1 等腰三角形学案及答案

这是一份人教版八年级上册13.3.1 等腰三角形学案及答案，共7页。学案主要包含了学习目标，要点梳理，典型例题，总结升华，思路点拨，答案与解析等内容，欢迎下载使用。
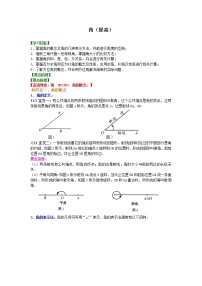
等腰三角形性质及判定（提高） 【学习目标】1. 掌握等腰三角形的性质，并能利用它证明两个角相等、两条线段相等以及两条直线垂直．2. 掌握等腰三角形的判定定理．3. 熟练运用等腰三角形的判定定理与性质定理进行推理和计算．【要点梳理】要点一、等腰三角形的定义有两条边相等的三角形，叫做等腰三角形，其中相等的两条边叫做腰，另一边叫做底，两腰所夹的角叫做顶角，底边与腰的夹角叫做底角.如图所示，在△ABC中，AB＝AC，则它叫等腰三角形，其中AB、AC为腰，BC为底边,∠A是顶角，∠B、∠C是底角．　　要点诠释：等腰直角三角形的两个底角相等，且都等于45°.等腰三角形的底角只能为锐角，不能为钝角（或直角），但顶角可为钝角（或直角）.∠A＝180°－2∠B，∠B＝∠C＝ .【高清课堂：389301 等腰三角形的性质及判定，知识要点】要点二、等腰三角形的性质1.等腰三角形的性质性质1：等腰三角形的两个底角相等（简称“等边对等角”）．性质2：等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合（简称“三线合一”）．2.等腰三角形的性质的作用性质1证明同一个三角形中的两角相等.是证明角相等的一个重要依据．性质2用来证明线段相等，角相等，垂直关系等．3.等腰三角形是轴对称图形等腰三角形底边上的高（顶角平分线或底边上的中线）所在直线是它的对称轴，通常情况只有一条对称轴．要点三、等腰三角形的判定如果一个三角形中有两个角相等，那么这两个角所对的边也相等（简称“等角对等边”）.    要点诠释：等腰三角形的判定是证明两条线段相等的重要定理，是将三角形中的角的相等关系转化为边的相等关系的重要依据.等腰三角形的性质定理和判定定理是互逆定理.【典型例题】类型一、等腰三角形中的分类讨论【高清课堂：389301 等腰三角形的性质及判定：例2（1）】 1、等腰三角形一腰上的高与另一腰的夹角为30°，则顶角的度数为(    )．        A．60°    B．120°    C．60°或150°    D．60°或120°【答案】D；【解析】由等腰三角形的性质与三角形的内角和定理可知，等腰三角形的顶角可以是锐角、直角、钝角，然而题目没说是什么三角形，所以分类讨论，画出图形再作答．(1)顶角为锐角如图①，按题意顶角的度数为60°；    (2)顶角为直角，一腰上的高是另一腰，夹角为0°不符合题意；    (3)顶角为钝角如图②，则顶角度数为120°，故此题应选D．【总结升华】这是等腰三角形按顶角分类问题，对于等腰三角形按顶角分：等腰锐角三角形、等腰直角三角形和等腰钝角三角形，故解此题按分类画出相应的图形再作答.举一反三：【变式】（2015•杭州校级二模）等腰三角形有一个外角是100°，这个等腰三角形的底角是　          　．【答案】50°或80°．解：①若100°的外角是此等腰三角形的顶角的邻角，则此顶角为：180°﹣100°=80°，则其底角为：（180°﹣80°）÷2=50°；②若100°的外角是此等腰三角形的底角的邻角，则此底角为：180°﹣100°=80°；故这个等腰三角形的底角为：50°或80°．故答案为：50°或80°．类型二、等腰三角形的操作题2、根据给出的下列两种情况，请用直尺和圆规找到一条直线，把△ABC恰好分割成两个等腰三角形（不写做法，但需保留作图痕迹，在图中标注分割后的角度）；并根据每种情况分别猜想：∠A与∠B有怎样的数量关系时才能完成以上作图？（1）如图①△ABC中，∠C＝90°，∠A＝24°；猜想：（2）如图②△ABC中，∠C＝84°，∠A＝24°；猜想：【思路点拨】在等腰三角形中，“等边对等角”与“等角对等边”，本题应从角度入手进行考虑.【答案与解析】（1）作图：猜想：∠A＋∠B＝90°，（2）作图：猜想：∠B＝3∠A.                              【总结升华】对图形进行分割是近年来出现的一类新题型，主要考查对基础知识的掌握情况以及动手实践能力，本类题目的答案有时不唯一.举一反三：【变式】直角三角形纸片ABC中，∠ACB＝90°，AC≤BC，如图，将纸片沿某条直线折叠，使点A落在直角边BC上，记落点为D，设折痕与AB、AC边分别交于点E、F，探究：如果折叠后的△CDF与△BDE均为等腰三角形，那么纸片中的∠B的度数是多少？写出你的计算过程，并画出符合条件的折叠后的图形．【答案】解：若△CDF是等腰三角形，则一定是等腰直角三角形.设∠B为度   ∠1＝45°，∠2＝∠A＝90°－①当BD＝BE时                                   ∠3＝  ，45°＋90°－＋＝180°，＝30° .                                          ②经计算ED＝EB不成立.③当DE＝DB时∠3＝180°－245°＋90°－＋180°－2＝180°，＝45°.综上所述，∠B＝30°或45°. 类型三、等腰三角形性质判定综合应用3、如图，△ABC中，∠C=2∠A，BD平分∠ABC交AC于D，求证：AB=CD+BC．（用两种方法）【思路点拨】方法一：先在AB上取BE=BC，根据SAS证出△CBD≌△EBD，得出CD=ED，∠C=∠BED，再证明∠A=∠ADE，得出AE=DE=CD，最后根据AB=BE+AE，即可得出答案；方法二：先延长BC至F，使CF=CD，得出∠F=∠CDF，再利用AAS证出△ABD≌△FBD，得出AB=BF，最后根据BF=BC+CF=BC+CD，即可得出答案．【答案与解析】解；方法一：在AB上取BE=BC，∵BD平分∠ABC交AC于D，∴∠CBD=∠EBD，∵在△CBD和△EBD中，，∴△CBD≌△EBD（SAS），∴CD=ED，∠C=∠BED，∵∠C=2∠A，∴∠BED=2∠A，∵∠BED=∠A+∠ADE，∴∠A=∠ADE，∴AE=DE，∴AE=CD，∵AB=BE+AE，∴AB=CD+BC；方法二：延长BC至F，使CF=CD，则∠F=∠CDF，∵∠ACB=∠F+∠CDF，∴∠ACB=2∠F，∴∠ACB=2∠A，∴∠A=∠F，在△ABD和△FBD中，，∴△ABD≌△FBD（AAS），∴AB=BF，∵BF=BC+CF，∴BF=BC+CD，∴AB=BC+CD．【总结升华】此题考查了等腰三角形的判定与性质，用到的知识点是三角形的外角、全等三角形的判定与性质、等腰三角形的判定与性质，关键是作出辅助线，构造全等三角形．举一反三：【变式】如图，已知AD是△ABC的中线，BE交AC于E，交AD于F，且AE＝EF．求证：AC＝BF．【答案】 证明：延长AD至点G，使DG＝AD，连接BG.                                4、如图，AC＝BC，∠ACB＝90°，∠A的平分线AD交BC于点D，过点B作BE⊥AD于点E.求证：BE＝AD. 【答案与解析】            证明：如图，延长BE、AC交于点F.∵∠1＝∠2，AE＝AE，∠AEB＝∠AEF＝90°，∴△AEB≌△AEF（ASA）.∴BE＝FE＝BF.∵∠3＝90°－∠F＝∠2，BC＝AC,∴△BCF≌△ACD（ASA）∴BF＝AD，BE＝AD.【总结升华】在几何解题的过程中，当遇到角分线或线段垂线时常考虑使用翻折变换，可保留原有图形的性质，且使原来分散的条件相对集中，以利于问题的解决．举一反三：【变式】已知，如图，AD为△ABC的内角平分线，且AD＝AB，CM⊥AD于M. 求证：AM＝(AB＋AC) ．【答案】证明：延长AM至点E，使ME＝AM，连接CE.                                       ∴