高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数多媒体教学课件ppt

这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.3 对数多媒体教学课件ppt，共37页。PPT课件主要包含了必备知识·探新知，nlogaM，关键能力·攻重难等内容，欢迎下载使用。

4.3.2　对数的运算
思考1：在积的对数运算性质中，三项的乘积式lga(MNQ)是否适用？你能得到一个怎样的结论？提示：适用，lga(MNQ)＝lgaM＋lgaN＋lgaQ，积的对数运算性质可以推广到真数是n个正数的乘积．
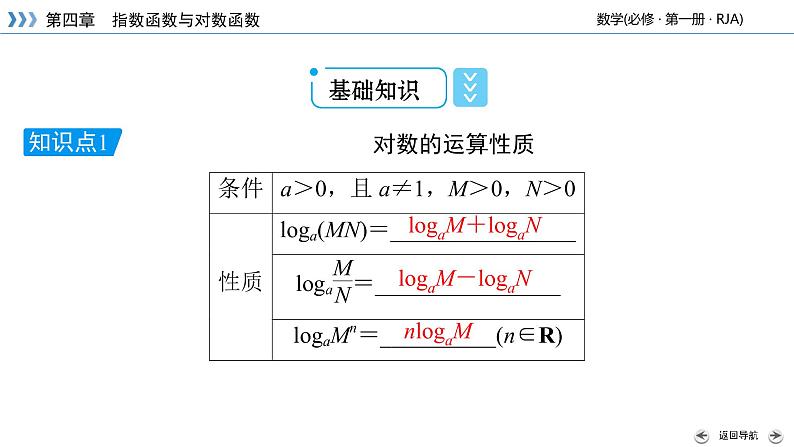
换底公式若a>0，且a≠1；b>0；c>0，且c≠1，则有lgab＝________.
2．lg62＋lg63等于(　　)A．1B．2C．5D．6[解析]　lg62＋lg63＝lg6(2×3)＝lg66＝1.
3．(2020·天津和平区高一期中测试)计算：lg25·lg32·lg59＝_____.
题型一　对数的运算性质的应用
[归纳提升]　对对数式进行计算、化简时，一要注意准确应用对数的性质和运算性质．二要注意取值范围对符号的限制．
题型二　利用对数的运算性质化简、求值
[分析]　熟练掌握对数的运算性质并能逆用性质是解题的关键．进行对数运算，要注意法则的正用和逆用．在化简变形的过程中，要善于观察、比较和分析，从而选择快捷、有效的运算方案．
[归纳提升]　利用对数运算性质化简与求值的原则(1)正用或逆用公式，对真数进行处理．(2)选哪种策略化简，取决于问题的实际情况，一般本着便于真数化简的原则进行．
(2)原式＝(lg5)2＋lg2×lg(5×10)＝(lg5)2＋lg2×(1＋lg5)＝(lg5)2＋lg2＋lg2·lg5＝lg5(lg5＋lg2)＋lg2＝lg5＋lg2＝lg10＝1.
[分析]　(1)对数的底数不同，如何将其化为同底的对数？(2)等式左边前一个对数的真数是后面对数的底数，利用换底公式很容易进行约分求解m的值．
题型三　换底公式的应用
忽视真数大于零致误解方程：lg2(x＋1)－lg4(x＋4)＝1.
[错因分析]　解题过程中忽视对数lgaN中真数N必须大于0时对数才有意义．实际上，在解答此类题时，要时刻关注对数本身是否有意义．另外，在运用对数运算性质或相关公式时也要谨慎，以防出错．
[方法点拨]　在将对数方程化为代数方程的过程中，未知数的范围扩大或缩小就容易产生增根．故解对数方程必须把所求的解代入原方程进行检验，否则易产生增根，造成解题错误．也可以像本题的求解过程这样，在限制条件下去求解．
[归纳提升]　1.应用换底公式应注意的事项(1)注意换底公式的正用、逆用以及变形应用．(2)题目中有指数式和对数式时，要注意将指数式与对数式统一成一种形式，注意转化与化归思想的运用．2．对数式的条件求值问题要注意观察所给数字特征，分析找到实现转化的共同点进行转化．3．利用换底公式计算、化简、求值的一般思路：思路一：用对数的运算法则及性质进行部分运算→换成同一底数．思路二：一次性统一换为常用对数(或自然对数)→化简、通分、求值．