沪科版八年级下册17.4 一元二次方程的根与系数的关系教学课件ppt

这是一份沪科版八年级下册17.4 一元二次方程的根与系数的关系教学课件ppt，共20页。PPT课件主要包含了–15，你能证你的猜想吗，解方程组得，本题还有别的解法吗，解得k7等内容，欢迎下载使用。

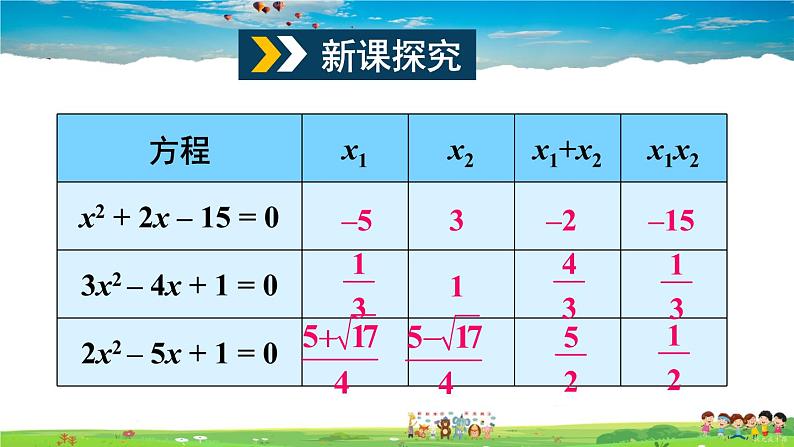
你是否注意到每个方程中的两根之间的关系？两根之和（x1 + x2）、两根之积（x1x2）与该方程的各项系数之间有怎样的关系？填写下表，然后观察根与系数的关系：
猜想：方程 ax2 + bx + c = 0（a ≠ 0）的根如果是 x1、x2，那么 x1+x2 =_____，x1x2 =_____.
我们知道，一元二次方 ax2+ bx + c = 0 （a ≠ 0）的两根为
当一元二次方程的二次项系数为 1 时，它的标准形式为 x2 + px + q = 0. 设它的两个根为 x1，x2，这时韦达定理应是：x1 + x2 = –p，x1x2 = q.
不解方程，求下列方程两根的和与积.
x2 – 3x = 15； 5x2 – 1 = 4x2 + x
解：x1 + x2 = 3 x1x2 = –15
解：化简得 x2 – x – 1 = 0 x1 + x2 = 1 x1x2 = –1
例 1 已知关于 x 的方程 2x2 + kx – 4 = 0 的一个根是 –4，求它的另一个根及 k 的值.
解 设方程的另一个根是 x2，则
解 将 x = –4 代入方程，得
2×（ –4 ）2 +（ –4 ）k – 4 = 0.
例 2 方程 2x2 – 3x + 1 = 0 的两个根记作x1，x2，不解方程，求 x1 – x2 的值.
（x1 – x2）2 =（x1 + x2）2 – 4x1x2
引申：若 ax2  bx  c  0（a  0   0）（1）若两根互为相反数，则 b  0；（2）若两根互为倒数，则 a  c；（3）若一根为 0，则 c  0；（4）若一根为 1，则 a  b  c  0；（5）若一根为 1，则 a  b  c  0；（6）若 a、c 异号，方程一定有两个实数根.
1. 关于 x 的方程 x2 + px + q = 0 的根为 x1 = 1+ ，x2 = 1 – ，则 p = ，q= . 2. 已知方程 5x2 + kx – 6 = 0 的一根是 2，则另一根是 ， k＝ .
3. 求下列方程的两根 x1，x2 的和与积： （1）x2 – 3x + 2 = 0； （2）x2 + x = 5x + 6
解：x1 + x2 = 3 x1x2 = 2
解：化简得 x2 – 4x – 6 = 0 x1 + x2 = 4 x1x2 = – 6
4. x1，x2 是方程 x2 – 5x – 7 = 0 的两根，不解方程求下列各式的值： （1） ；（2） .
解：∵ x1，x2 是方程 x2 – 5x – 7 = 0 的两根. 则 x1 + x2 = 5，x1x2 = – 7 .
5. 已知关于 x 的方程 x2 –（2m + 3）x + m2 = 0 的两根之和等于两根之积，求 m 的值.
解：设方程 x2 – （2m + 3）x + m2 = 0 的两根为 x1，x2. ∴ x1 + x2 = 2m + 3，x1x2 = m2. 根据题意得 m2 = 2m +3，解得 m1= 3，m2 = – 1. 当 m = 3 时，原方程为 x2 – 9x + 9 = 0，b2 – 4ac = 45 > 0. 方程有实数根. 当 m = –1 时，原方程为 x2 – x + 1 = 0，b2 – 4ac = – 3 < 0. 方程无实数根，此 m 值舍去. ∴ m 的值为 3.