高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数当堂检测题

这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数当堂检测题，共7页。试卷主要包含了函数y＝lga＋1的图象过定点，已知lgb＜lga＜lgc，则，2，b＝20等内容，欢迎下载使用。
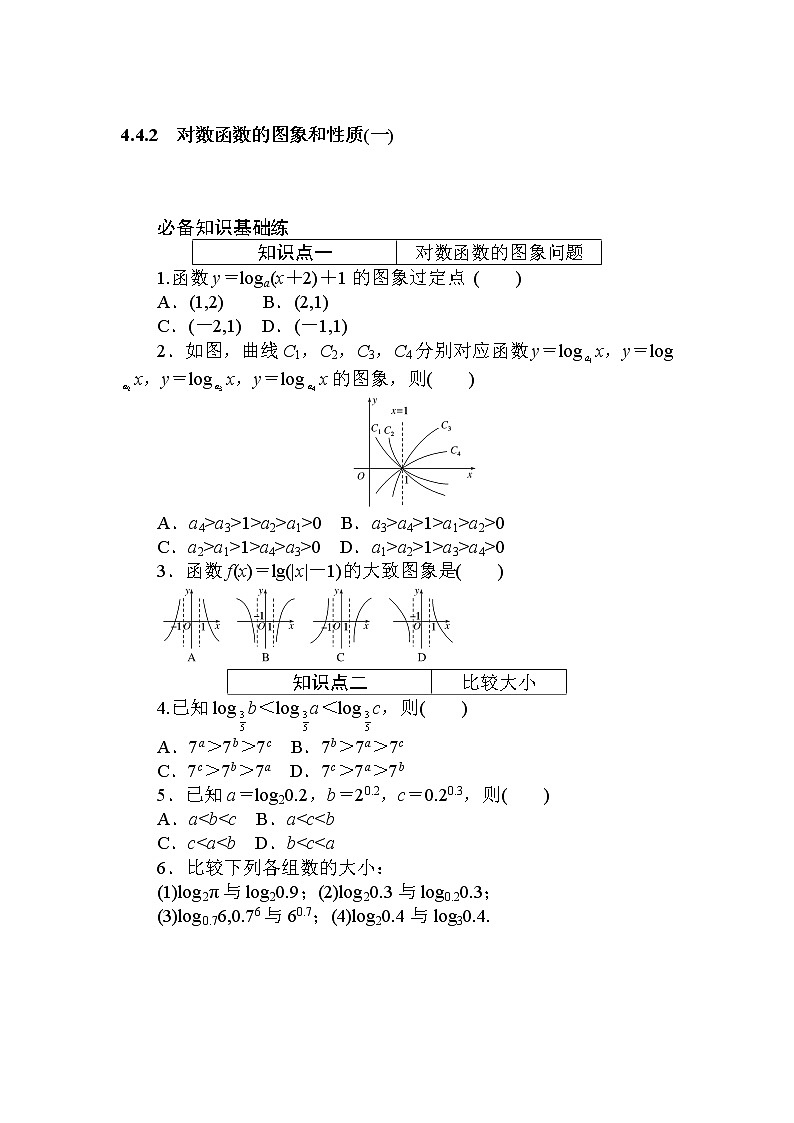
4.4.2　对数函数的图象和性质(一) 　必备知识基础练知识点一对数函数的图象问题1.函数y＝loga(x＋2)＋1的图象过定点 (　　)A．(1,2)    B．(2,1)C．(－2,1)  D．(－1,1)2．如图，曲线C1，C2，C3，C4分别对应函数y＝logx，y＝logx，y＝logx，y＝logx的图象，则(　　)A．a4>a3>1>a2>a1>0  B．a3>a4>1>a1>a2>0C．a2>a1>1>a4>a3>0  D．a1>a2>1>a3>a4>03．函数f(x)＝lg(|x|－1)的大致图象是(　　)知识点二比较大小4.已知logb＜loga＜logc，则(　　)A．7a＞7b＞7c  B．7b＞7a＞7cC．7c＞7b＞7a  D．7c＞7a＞7b5．已知a＝log20.2，b＝20.2，c＝0.20.3，则(　　)A．a<b<c  B．a<c<bC．c<a<b  D．b<c<a6．比较下列各组数的大小：(1)log2π与log20.9；(2)log20.3与log0.20.3；(3)log0.76,0.76与60.7；(4)log20.4与log30.4.       知识点三反函数7.已知函数y＝ax与y＝logax，其中a>0且a≠1，下列说法不正确的是(　　)A．两者的图象关于直线y＝x对称B．前者的定义域、值域分别是后者的值域、定义域C．两函数在各自的定义域内增减性相同D．y＝ax的图象经过平行移动可得到y＝logax的图象8．函数y＝f(x)是g(x)＝logx的反函数，则f(2)＝________.   关键能力综合练一、选择题1．若函数y＝f(x)是函数y＝ax(a>0，且a≠1)的反函数且f(2)＝1，则f(x)＝(　　)A．log2x   B.C．logx  D．2x－22．若0<a<1，则函数y＝loga(x＋5)的图象不经过(　　)A．第一象限  B．第二象限C．第三象限  D．第四象限3．已知logm<logn<0，则(　　)A．n<m<1  B．m<n<1C．1<m<n  D．1<n<m4．设a＝log36，b＝log510，c＝log714，则(　　)A．c>b>a  B．b>c>aC．a>c>b  D．a>b>c5．若函数f(x)＝loga(x＋b)的图象如图，其中a，b为常数，则函数g(x)＝ax＋b的图象大致是(　　)6．已知实数a＝log45，b＝0，c＝log30.4，则a，b，c的大小关系为(　　)A．b<c<a  B．b<a<cC．c<a<b  D．c<b<a二、填空题7．函数y＝loga(x－4)＋2(a>0且a≠1)恒过定点________．8．(易错题)已知f(x)＝|log3x|，若f(a)＞f(2)，则a的取值范围为________．9．(探究题)已知函数f(x)＝，则f(8)＝________，若直线y＝m与函数f(x)的图象只有1个交点，则实数m的取值范围是________．三、解答题10．已知函数f(x)＝loga(x－1)的图象过点(3,1)．(1)求函数f(x)的解析式；(2)若f(m)≤f(2)，求m的取值集合．       学科素养升级练1．(多选题)已知函数f(x)＝，若x1<x2<x3<x4，且f(x1)＝f(x2)＝f(x3)＝f(x4)，则下列结论正确的是(　　)A．x1＋x2＝－1  B．x3x4＝1C．1<x4<2       D．0<x1x2x3x4<12．(学科素养—数学抽象)若函数f(x)＝log2x＋2的反函数的定义域为(3，＋∞)，则此函数的定义域为________．f－1(4)＝________.3．已知函数f(x)＝|logx|.(1)画出函数y＝f(x)的图象； (2)写出函数y＝f(x)的单调区间；(3)当x∈时，函数y＝f(x)的值域为[0,1]，求m的取值范围．                  4．4.2　对数函数的图象和性质(一)必备知识基础练1．解析：令x＋2＝1，即x＝－1，得y＝loga1＋1＝1，故函数y＝loga(x＋2)＋1的图象过定点(－1,1)．答案：D2．解析：作直线y＝1，它与各曲线C1，C2，C3，C4的交点的横坐标就是各对数的底数，由此可判断出各底数的大小必有a4>a3>1>a2>a1>0.答案：A3．解析：由f(－x)＝lg(|－x|－1)＝lg(|x|－1)＝f(x)，得f(x)是偶函数，由此知C、D错误．又当x＞0时，f(x)＝lg(x－1)是(1，＋∞)上的增函数，故选B.答案：B4．解析：由于函数y＝logx为减函数，因此由logb＜loga＜logc可得b＞a＞c，又由于函数y＝7x为增函数，所以7b＞7a＞7c.答案：B5．解析：∵a＝log20.2<0，b＝20.2>1，c＝0.20.3∈(0,1)，∴a<c<b.故选B.答案：B6．解析：(1)因为函数y＝log2x在(0，＋∞)上是增函数，π＞0.9，所以log2π＞log20.9.(2)由于log20.3＜log21＝0，log0.20.3＞log0.21＝0，所以log20.3＜log0.20.3.(3)因为60.7＞60＝1,0＜0.76＜0.70＝1，又log0.76＜log0.71＝0，所以60.7＞0.76＞log0.76.(4)底数不同，但真数相同，根据y＝logax的图象在a＞1,0＜x＜1时，a越大，图象越靠近x轴，知log30.4＞log20.4.7．解析：由反函数的定义可知ABC均正确，D错误．答案：D8．解析：f(x)＝x，f(2)＝2＝.答案：关键能力综合练1．解析：∵y＝ax的反函数为y＝logax，∴f(x)＝logax，∵f(2)＝1，即loga2＝1，∴a＝2，则f(x)＝log2x，选A.答案：A2．解析：∵y＝loga(x＋5)过定点(－4,0)且单调递减，∴函数图象不过第一象限，故选A.答案：A3．解析：因为0<<1，logm<logn<0，所以m>n>1，故选D.答案：D4．解析：a＝log36＝log32＋1，b＝log52＋1，c＝log72＋1，在同一坐标系内分别画出y＝log3x，y＝log5x，y＝log7x的图象，当x＝2时，由图易知log32>log52>log72，∴a>b>c.答案：D5．解析：由函数f(x)＝loga(x＋b)的图象可知，函数f(x)＝loga(x＋b)在(－b，＋∞)上是减函数．∴0<a<1且0<b<1.所以g(x)＝ax＋b在R上是减函数，故排除A、B.由g(x)的值域为(b，＋∞)．所以g(x)＝ax＋b的图象应在直线y＝b的上方，故排除C.答案：D6．解析：由题意知，a＝log45>1，b＝0＝1，c＝log30.4<0，故c<b<a.答案：D7．解析：令x－4＝1得x＝5，此时y＝loga1＋2＝2，所以函数y＝loga(x－4)＋2恒过定点(5,2)．答案：(5,2)8．解析：作出函数f(x)的图象，如图所示，由于f(2)＝f，故结合图象可知0＜a＜或a＞2.答案：∪(2，＋∞)9．解析：当x＝8时，f(8)＝log28＝3；作出函数f(x)的图象，如图所示，若直线y＝m与函数f(x)的图象只有1个交点，由图象可知，当m≥2或m＝0时满足条件，故答案为：3；{0}∪[2，＋∞)．答案：3　{0}∪[2，＋∞)10．解析：(1)由函数f(x)＝loga(x－1)的图象过点(3,1)，得a＝2.所以函数解析式为f(x)＝log2(x－1)．(2)若f(m)≤f(2)，由f(x)在(1，＋∞)上单调递增，得1<m≤2.所以m的取值集合为{m|1<m≤2}．学科素养升级练1．解析：由函数f(x)＝，作出其函数图象：由图可知，x1＋x2＝－2，－2<x1<－1；当y＝1时，|log2x|＝1，有x＝，2；所以<x3<1<x4<2；由f(x3)＝f(x4)有|log2x3|＝|log2x4|，即log2x3＋log2x4＝0； 所以x3x4＝1；则x1x2x3x4＝x1x2＝x1(－2－x1)＝－(x1＋1)2＋1∈(0,1)；故选：BCD.答案：BCD2．解析：函数f(x)＝log2x＋2的反函数的定义域(3，＋∞)为函数f(x)的值域，由log2x＋2＞3，得log2x＞1，x∈(2，＋∞)，由log2x＋2＝4，得x＝22＝4，故答案为：(2，＋∞)；4.答案：(2，＋∞)　43．解析：(1)先作出y＝logx的图象，再把y＝logx的图象x轴下方的部分往上翻折，得到f(x)＝|logx|的图象如图．(2)f(x)的定义域为(0，＋∞)，由图可知，f(x)在(0,1)上单调递减，在(1，＋∞)上单调递增．(3)由f(x)＝|logx|的图象可知f＝f(2)＝1，f(1)＝0，由题意结合图象知，1≤m≤2.