2021学年5 三角函数的应用说课课件ppt

这是一份2021学年5 三角函数的应用说课课件ppt，共14页。PPT课件主要包含了情景导入，探索新知，随堂练习，课堂小结等内容，欢迎下载使用。

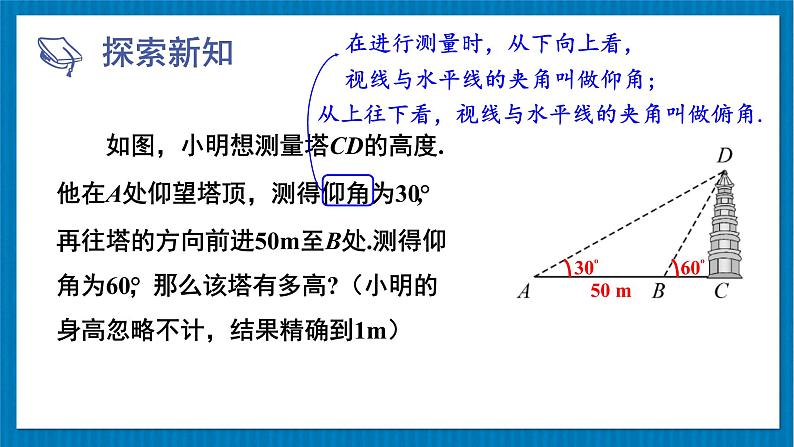
如图，小明想测量塔CD的高度.
他在A处仰望塔顶，测得仰角为30°,
再往塔的方向前进50m至B处.测得仰角为60°，那么该塔有多高?（小明的身高忽略不计，结果精确到1m）
在进行测量时，从下向上看，视线与水平线的夹角叫做仰角;
从上往下看，视线与水平线的夹角叫做俯角.
解：如图∠DAC=30°，∠DBC=60°，AB=50m，设塔高DC=x m.
Rt△ADC中, .
Rt△BDC中, .
∴AB=AC－BC= .
∴x= ≈43(m).
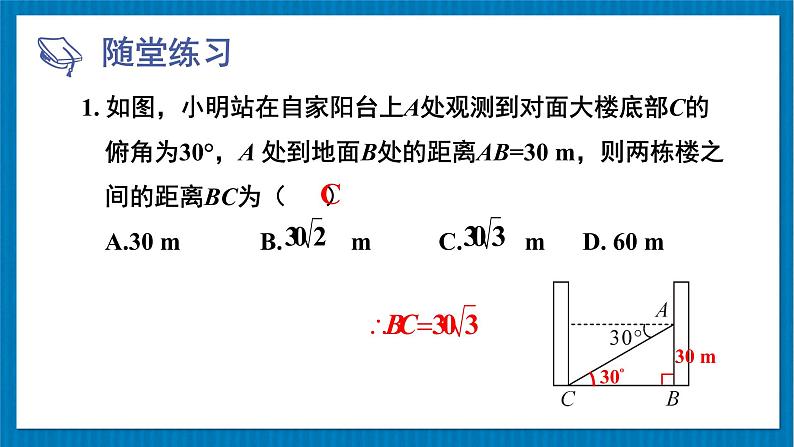
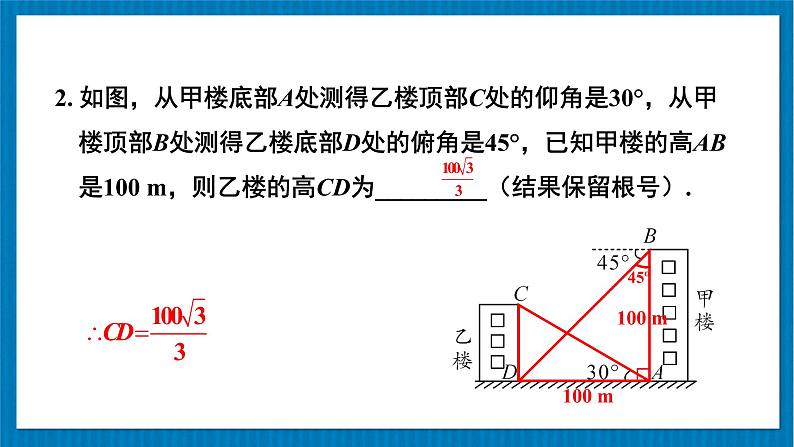
2. 如图，从甲楼底部A处测得乙楼顶部C处的仰角是30°，从甲楼顶部B处测得乙楼底部D处的俯角是45°，已知甲楼的高AB是100 m，则乙楼的高CD为_________（结果保留根号）.
3.[内江中考]如图，有两座建筑物DA 与CB，其中 CB的高为120 m，从DA 的顶点A测得CB顶部B的仰角为30°，测得其底部C的俯角为45°，这两座建筑物的地面距离DC为多少米？（结果保留根号）
解：如图所示，过点A作AE⊥BC，垂足为E.
则四边形ADCE为矩形，∴AE=DC.
在Rt△ABE中，∠BAE=30°,
解：如图所示，过点B作BM⊥CQ，垂足为M.
在Rt△ACP中，∠APC=∠α=74°，
在Rt△BMQ中，∠BQM=∠β=30°，
答：这座大桥PQ的长度约为1229m.
4. 如图，一灯柱AB被一钢缆CD固定，CD与地面成40°夹角，且DB=5m.在C点上方2m处加固另一条钢缆ED，那么钢缆ED的长度为多少？（结果精确到0.01m）
解：在Rt△CBD中，∵BC=5tan40°≈4.195（m），
∴EB=EC+CB=2+4.195=6.195（m）.
∴钢缆ED的长度约为7.96m.
通过本节课的学习，你有哪些收获？
数学源于生活 又服务于生活