初中数学北师大版九年级下册第三章 圆2 圆的对称性图片课件ppt

这是一份初中数学北师大版九年级下册第三章 圆2 圆的对称性图片课件ppt，共24页。PPT课件主要包含了新课导入，探究新知，圆心角的概念，∠AOB，∠COD，∠AOC，∠BOD，随堂练习，课堂小结，等对等定理等内容，欢迎下载使用。

（1）圆是轴对称图形吗？如果是，它的对称轴是什么？（2）你是用什么办法解决上述问题的？与同伴进行交流.
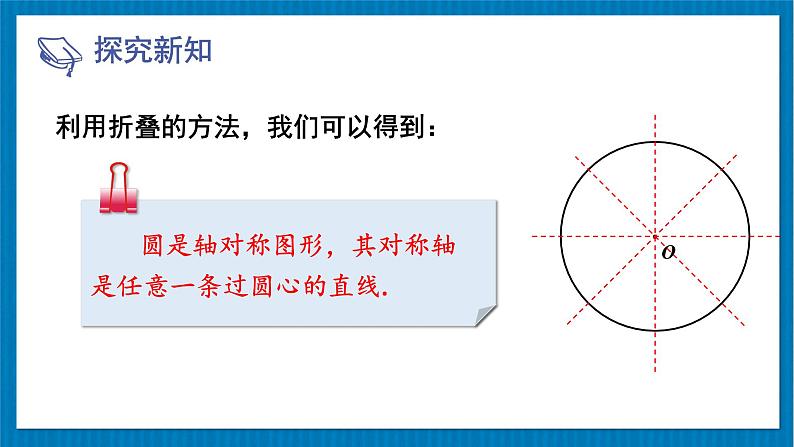
利用折叠的方法，我们可以得到：
圆是轴对称图形，其对称轴是任意一条过圆心的直线.
一个圆绕着它的圆心任意旋转一个角度，还能与原来的图形重合吗？
一个圆绕着它的圆心旋转任意一个角度，都能与原来的图形重合.特别地，
圆是中心对称图形，对称中心为圆心.
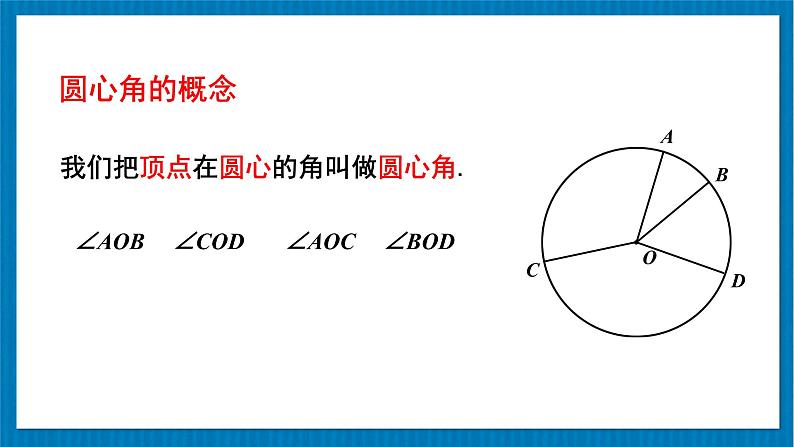
我们把顶点在圆心的角叫做圆心角.
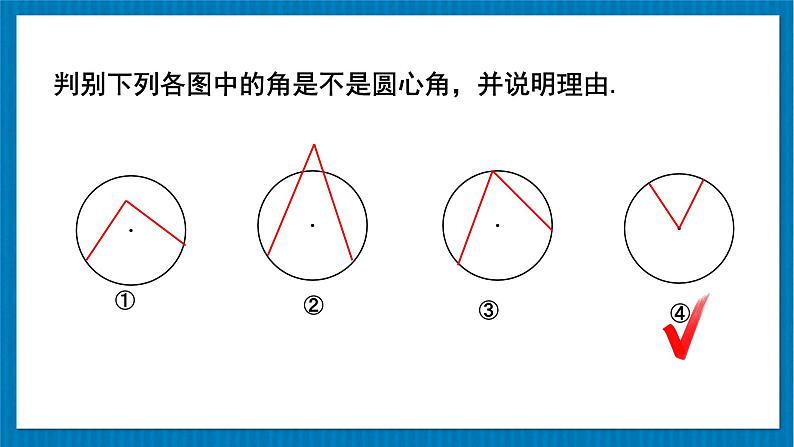
判别下列各图中的角是不是圆心角，并说明理由.
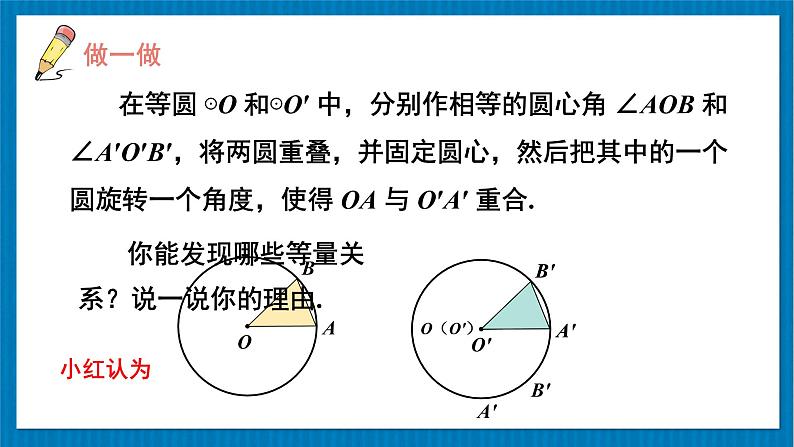
在等圆 ⊙O 和⊙O′ 中，分别作相等的圆心角 ∠AOB 和∠A′O′B′，将两圆重叠，并固定圆心，然后把其中的一个圆旋转一个角度，使得 OA 与 O′A′ 重合.
你能发现哪些等量关系？说一说你的理由.
她是这样想的：∵ 半径 OA 与 O′A′ 重合，∠AOB = ∠A′O′B′，∴ 半径 OB 与 O′B′ 重合.∵ 点 A 与点 A′ 重合，点 B 与 点B′ 重合，
在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等.
∵∠AOB=∠A′OB′
在同圆或等圆中，如果两个圆心角所对的弧相等，那么它们所对的弦相等吗？这两个圆心角相等吗？你是怎么想的？
在同圆或等圆中，如果两条弦相等，你能得出什么结论？
在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等.
（1）∵ AB=A′B′， ∴
（2）∵ ， ∴
（3）∵ ， ∴
例 如图，AB、DE 是 ⊙O 的直径，C 是⊙O 上的一点，且 . BE 与 CE 的大小有什么关系？为什么？
解：BE = CE．理由是：
∵ ∠AOD =∠BOE，∴ BE = CE．
1. 下列说法正确的是（ ）A. 相等的圆心角所对的弧相等B. 在同圆中，等弧所对的圆心角相等C. 相等的弦所对的圆心到弦的距离相等D. 圆心到弦的距离相等，则弦相等
注意前提“在同圆和等圆中”
2.日常生活中的许多图案或现象都与圆的对称性有关，试举几例.
解：如碗口、圆桌、圆桌上的转盘、方向盘等.（答案不唯一）
3.利用一个圆及其若干条弦分别设计出符合下列条件的图案：（1）是轴对称图形但不是中心对称图形；（2）是中心对称图形但不是轴对称图形；（3）既是轴对称图形又是中心对称图形.
4.已知A，B是⊙O上的两点，∠AOB=120°，C是AB的中点.试确定四边形OACB的形状，并说明理由.
解：四边形OACB是菱形.理由如下：如图所示，连接OC.
∴∠AOC=∠BOC.
又∵∠AOB=120°，∴∠AOC=∠BOC=60°.
∵OB=OC，OA=OC，∴△BCO和△ACO都是等边三角形.
∴OB=BC=CA=AO，∴四边形OACB是菱形.
5. 如图，AB、AC、BC 都是 ⊙O 的弦，∠AOC = ∠BOC，∠ABC 与∠BAC 相等吗？为什么？
解：∵∠AOC =∠BOC，∴AC = BC（在同圆或等圆中，如果圆心角相等，那么它们所对的弧相等，所对的弦相等）.∴∠ABC =∠BAC.
6.如图，AB 是 O 的直径，OD∥AC. 的大小有什么关系？为什么？
理由：连接OC，则∠OAC =∠OCA，∵AC∥OD，∴∠OCA =∠COD ∠OAC =∠BOD，∴∠COD =∠BOD，