【专项练习】苏教版初二数学上册 《勾股定理》模型（8）——垂美四边形模型（含答案）学案

这是一份【专项练习】苏教版初二数学上册 《勾股定理》模型（8）——垂美四边形模型（含答案）学案，共7页。
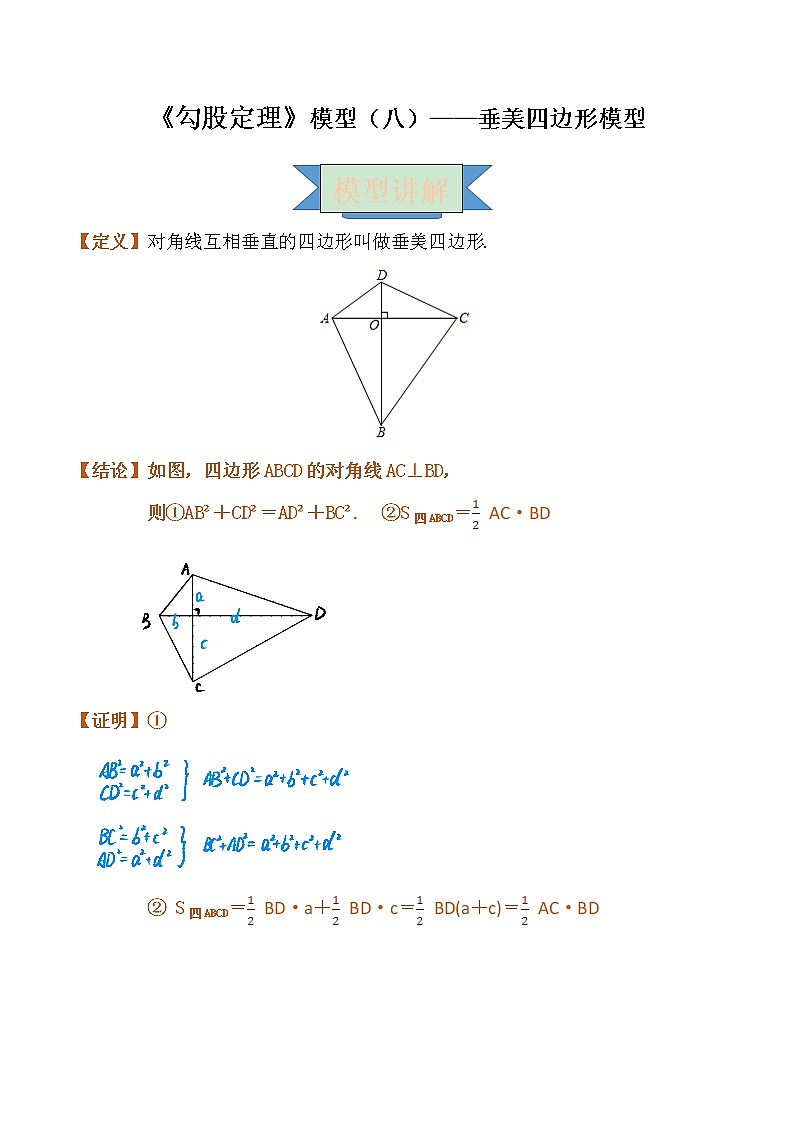
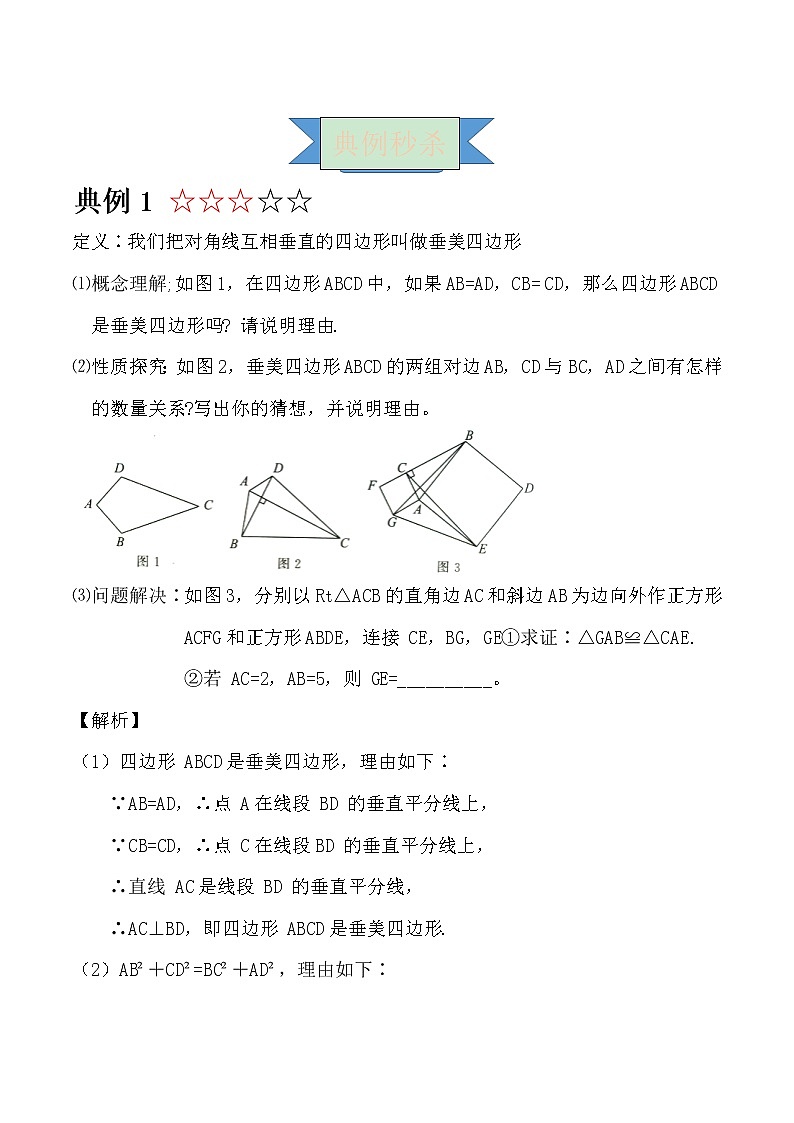
《勾股定理》模型（八）——垂美四边形模型   【定义】对角线互相垂直的四边形叫做垂美四边形.【结论】如图，四边形ABCD的对角线AC⊥BD，则①AB²＋CD²＝AD²＋BC².  ②S四ABCD＝ AC·BD【证明】①② S四ABCD＝ BD·a＋ BD·c＝ BD(a＋c)＝ AC·BD     典例1 ☆☆☆☆☆定义∶我们把对角线互相垂直的四边形叫做垂美四边形⑴概念理解;如图1，在四边形 ABCD中，如果 AB=AD，CB= CD，那么四边形 ABCD是垂美四边形吗? 请说明理由.⑵性质探究：如图2，垂美四边形ABCD的两组对边AB，CD与 BC，AD之间有怎样的数量关系?写出你的猜想，并说明理由。⑶问题解决∶如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连接 CE，BG，GE①求证∶△GAB≌△CAE.②若 AC=2，AB=5，则 GE=__________。【解析】（1）四边形 ABCD是垂美四边形，理由如下∶∵AB=AD，∴点 A在线段 BD 的垂直平分线上， ∵CB=CD，∴点 C在线段BD 的垂直平分线上， ∴直线 AC是线段 BD 的垂直平分线，∴AC⊥BD，即四边形 ABCD是垂美四边形.（2）AB²＋CD²=BC²＋AD²，理由如下∶如图，∵AC⊥BD，∴∠AED=∠AEB=∠BEC=∠CED=90°.由勾股定理得 AD²＋ BC²= AE²＋DE²＋BE²＋CE²,AB²＋CD²=AE²＋BE²＋CE²＋DE²,∴AB²＋CD²=BC²＋AD².（3）如图，①连接 CG，BE.∵∠CAG=∠BAE=90°,∴∠CAG＋∠BAC=∠BAE＋∠BAC,即∠GAB=∠CAE.在△GAB 和△CAE 中，AG=AC,∠GAB=∠CAE,AB=AE,    ∴△GAB≌△CAE(SAS).②∵△GAB≌△CAE，∴∠ABG=∠AEC，又∵∠AEC＋∠AME=90°，∠BMC=∠AME，∴∠ABG＋∠BMC=90°，∴∠BNC=90°，即 CE⊥BG，∴四边形CGEB是垂美四边形，∴CG²＋BE²=CB²+GE²∵AC=2,AB=5,∴BC=,CG=2,BE=5, ∴GE²=CG²＋BE²-CB²=37，∴GE=.典例2 ☆☆☆☆☆如图，△AOB和△COD都是等边三角形，AO=BO=2，CO=DO=1求AC²＋BD²   1.（★★★★★）数学活动∶图形的变化问题情境∶如图1，△ABC为等腰直角三角形，∠ACB=90º，E是AC边上的一个动点(点E与A，C不重合），以CE为边在△ABC外作等腰直角△ECD，∠ECD=90°，连接 BE，AD.猜想线段 BE，AD 之间的关系.（1）独立思考∶请直接写出线段 BE，AD 之间的关系.（2）合作交流∶“希望”小组受上述问题的启发，将图1中的等腰直角△ECD绕着点C顺时针方向旋转至如图2的位置，BE交AC于点H,交AD于点O.（1）中的结论是否仍然成立?请说明理由.（3）拓展延伸∶“科技”小组将⑵中的等腰直角△ABC改为Rt△ABC，∠ACB=90°，AC=8，BC=6，将等腰直角△ECD改为 Rt△ECD，∠ECD=90°，CD=4，CE=3.试猜想 BD²＋AE²是否为定值，结合图3说明理由.      1.在四边形 ABCD 中，AC⊥BD，AB=7，CD=11，BC=13，则AD=_______. 勾股定理是计算的工具 ，识别环境和了解模型背后约结论至关重要，等腰直角三角形手拉手全等模型容易出现垂美四边形     答案：小试牛刀 解析 （1）BE=AD，BE⊥AD.∵△ABC和△CDE都是等腰直角三角形，∴BC=AC,CE=CD,∠BCE=∠ACD= 90°,∴△BCE≌△ACD,∴BE=AD,∠CEB= ∠CDA.∴∠CBE ＋ ∠CEB = 90°,∴∠CBE＋∠CDA=90°, ∴BE⊥AD.（2）（1）中的结论仍然成立，理由∶∵△ABC是等腰直角三角形，∠ACB= 90°,∴AC=BC.∵△CDE是等腰直角三角形，∠ECD= 90°,∴CD=CE,∴∠ACB＋∠ACE=∠ECD+∠ACE, ∴∠BCE=∠ACD,∴△BCE≌△ACD,∴BE=AD,∠CBE=∠CAD.∵∠BHC=∠AHO,∠CBH＋∠BHC=90°,∴∠CAD＋∠AHO=90°,∴∠AOH=90, ∴BE⊥AD.（3）是定值，理由∶∵∠ECD=90°,∠ACB=90°, ∴∠ACB=∠ECD,∴∠ACB＋∠ACE=∠ECD＋∠ACE， ∴∠BCE=∠ACD.∵AC=8,BC=6,CD=4,CE=3, ∴BC:AC=CE:CD=3:4,∴△BCE∽△ACD,∴∠CBE=∠CAD.∵∠BHC=∠AHO, ∠CBH＋∠BHC=90°，∴∠CAD＋∠AHO=90°,∴∠AOH=90°,∴BE⊥AD,∴∠BOD=∠AQE=90°, ∴BD²=OB²＋OD²，AE²=OA²＋OE²， AB²=OA²+OB²，DE²=OE²+OD²，∴BD²＋AE²=OB²＋OD²＋OA²＋OE²= AB²＋DE²,在 Rt△ABC中，∠ACB=90°，AC=8，BC=6,∴AB²=100,在 Rt△ECD中，∠ECD=90°，CD=4，CE= 3,∴DE=25,∴BD²＋AE²=AB²＋DE²=125.直击中考 答案 1解析∵AC⊥BD，∴四边形 ABCD是垂美四边形，∴AB²＋CD²=AD²＋BC²， ∴AD=＝1.