2020-2021学年2 二次函数的图像与性质课文内容课件ppt

这是一份2020-2021学年2 二次函数的图像与性质课文内容课件ppt，共32页。PPT课件主要包含了学习目标，情境引入，新课讲解，y轴就是它的对称轴，原点00，位置开口方向，对称性，顶点最值，增减性，开口向上在x轴上方等内容，欢迎下载使用。

1.会画二次函数y=ax2和y=ax2+c的图象.（难点）2.掌握二次函数y=ax2和y=ax2+c的性质并会应用.（重点）3.比较函数y=ax2与y=ax2+c的联系.
门禁反映了图形的平移，大家还记得平移的要点吗？
羽毛球的运动轨迹可以用y=ax2的图象刻画,大家能回忆出二次函数y=x2的性质吗？
如果二次函数y=ax2的图象与平移碰撞在一起,会擦出怎样的火花呢？让我们拭目以待吧！
二次函数y=ax2的图象与性质
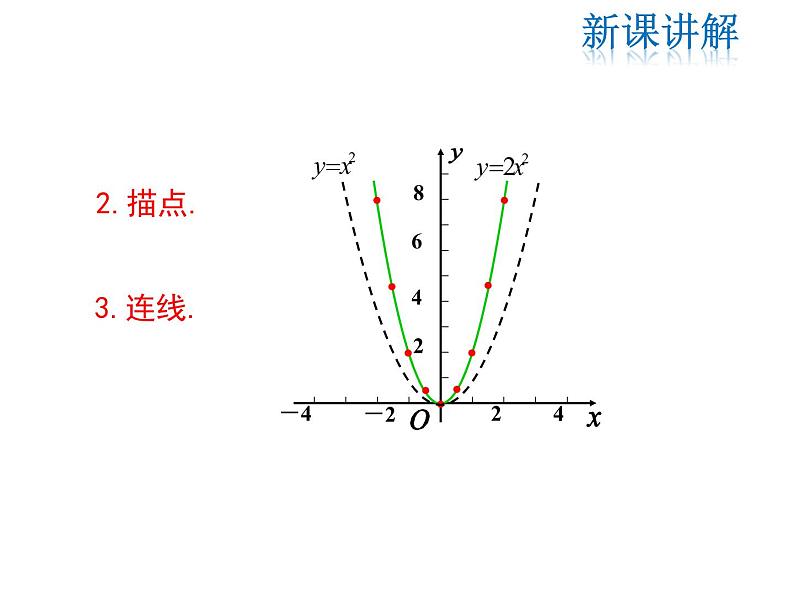
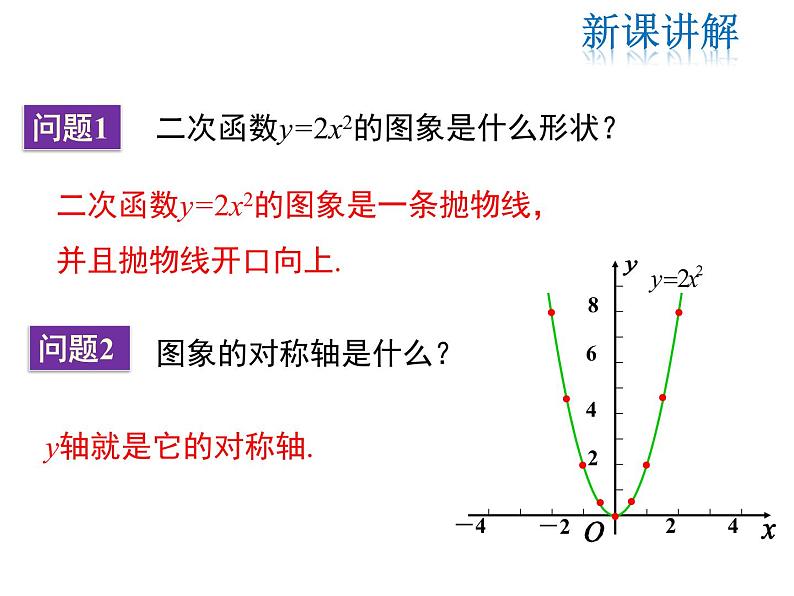
二次函数y=2x2的图象是一条抛物线，并且抛物线开口向上.
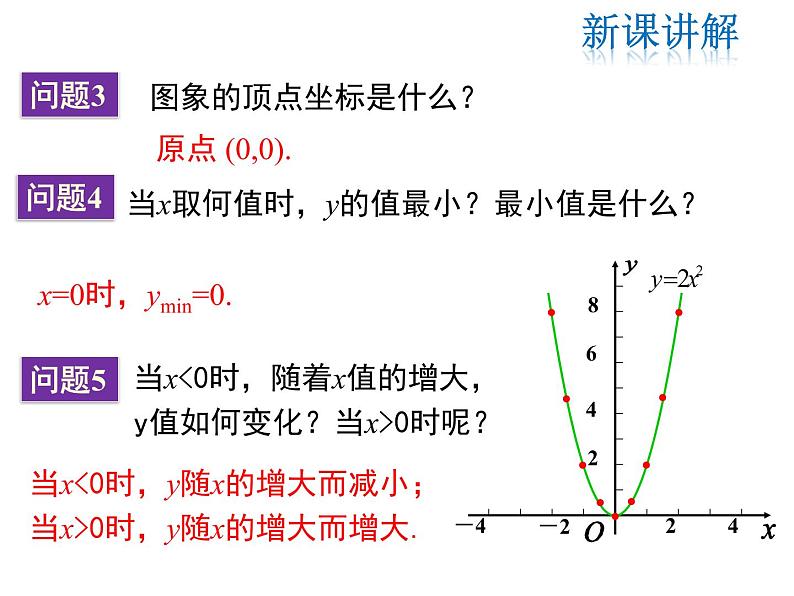
x=0时，ymin=0.
当x<0时，y随x的增大而减小；当x>0时，y随x的增大而增大.
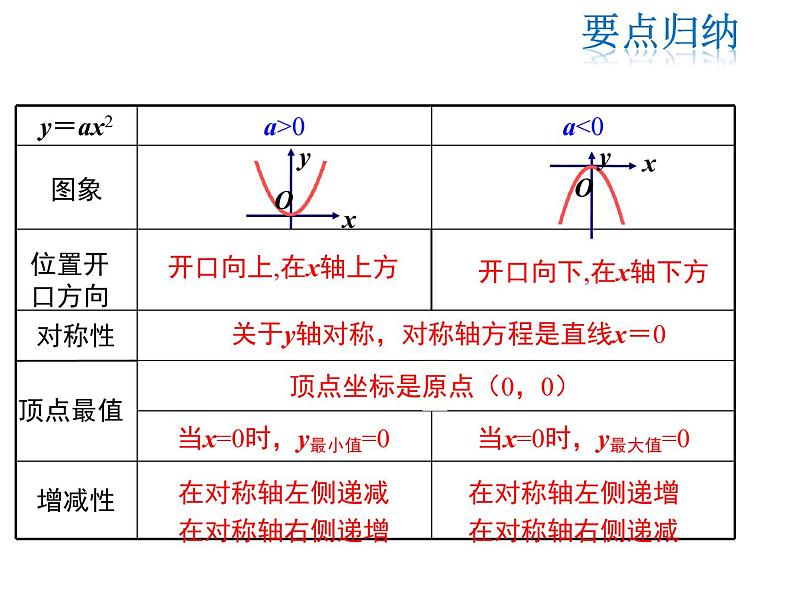
关于y轴对称，对称轴方程是直线x＝0
当x=0时，y最小值=0
当x=0时，y最大值=0
在对称轴左侧递减在对称轴右侧递增
在对称轴左侧递增在对称轴右侧递减
顶点坐标是原点（0，0）
3.函数y= x2的图象的开口 ,对称轴是 ,顶点 是 ;顶点是抛物线的最____点.
2.函数y=－3x2的图象的开口 ,对称轴是 , 顶点是_____ 顶点是抛物线的最____点
1.函数y=4x2的图象的开口 ,对称轴是 ,顶点 是 ;
4.函数y= －0.2x2的图象的开口 ,对称轴是_ __, 顶点是 ;
5.关于二次函数y＝2x2，下列说法正确的是(　) A．它的开口方向是向下 B．当x<0时，y随x的增大而减小 C．它的对称轴是x＝2 D．当x＝0时，y有最大值是0
若点(x1,y1)，B(x2,y2)是二次函数y=－3x2图象上的 两点，且x1＞x2＞0，那么y1与y2的大小关系是_____________.
因为y=－3x2的二次项系数为－3，－3小于0，则当x大于0时，y随x的增大而减小。
分析： 是二次函数，即二次项的系数不为0，x的指数等于2.又因当x＞0时，y随x增大而增大,即说明二次项的系数大于0.因此，
当a>0时，a的绝对值越大，开口越小.
当a<0时，a的绝对值越大，开口越小.
在二次函数y=ax2中，a的绝对值越大，开口越小.
把图中图象的号码，填在它的函数式后面：（填序号）（1）y=3x2的图象是_______；（2）y= x2的图象是_______；（3）y=－x2的图象是_______；（4）y= x2的图象是_______．
二次函数y=ax2＋c的图象与性质
在同一直角坐标系中，画出二函数 y=2x2＋1与y=2x2－1的图象．
抛物线 y=2x2＋1,y=2x2－1与抛物线y=2x2 有什么关系？
可以发现，把抛物线y=2x2 向 平移1个单位长度，就得到抛物线 ；把抛物线 y=2x2 向 平移1个单位长度，就得到抛物线 y=2x2-1.
1.二次函数y=ax2+c的图象可以由 y=ax2 的图象平移 得到： （1）当c > 0 时,向上平移c个单位长度得到. （2）当c < 0 时,向下平移-c个单位长度得到.
二次函数y=ax2 与y=ax2+c（a ≠ 0）的图象的关系
2.上下平移规律： 平方项不变，常数项上加下减.
二次函数y＝－3x2＋1的图象是将(　　) A．抛物线y＝－3x2向左平移3个单位得到 B．抛物线y＝－3x2向左平移1个单位得到 C．抛物线y＝3x2向上平移1个单位得到 D．抛物线y＝－3x2向上平移1个单位得到
抛物线y=2x2＋1,y=2x2－1的开口方向、对称轴和顶点各是什么？
抛物线y=2x2+1,y=2x2－1的增减性又如何？
当x=0时，y有最小值.
当x<0时，y随x的增大而减小； 当x>0时，y随x的增大而增大.
二次函数 y=ax2+c的性质
当x=0时，y最小值=c
当x=0时，y最大值=c
当x＜0时，y随x的增大而减小；x＞0时，y随x的增大而增大.
当x＞0时，y随x的增大而减小；x＜0时，y随x的增大而增大.
1.画抛物线y=ax2+c的图象有些方法？
2.抛物线y=ax2+c 中的a决定什么？c决定什么？它的对 称轴是什么？顶点坐标怎样表示？
第一种方法：平移法，两步即第一步画y=ax2的图象， 再向上（或向下）平移︱c ︱单位.
第二种方法：描点法，三步即列表、描点和连线.
a决定开口方向和大小；c决定顶点的纵坐标.对称轴为y轴；顶点坐标为(0,c).
如图，抛物线y＝x2－4与x轴交于A、B两点，点P为抛物线上一点，且S△PAB＝4，求P点的坐标．
解：抛物线y＝x2－4，令y＝0，得到x＝2或－2，即A点的坐标为(－2，0)，B点的坐标为(2，0)，∴AB＝4.∵S△PAB＝4，设P点纵坐标为b，∴ ×4|b|＝4，∴|b|＝2，即b＝2或－2.当b＝2时，x2－4＝2，解得x＝± ，此时P点坐标为( ，2)，(－ ，2)；当b＝－2时，x2－4＝－2，解得x＝± ，此时P点坐标为( ，2)，(－ ，2)．
1.抛物线y=2x2向下平移4个单位，就得到抛物 线 .　　
3.已知（m,n)在y=ax2+a（a不为0）的图象上，(－m,n) ___（填“在”或“不在”）y=ax2+a（a不为0）的 图象上.4. 若y=x2＋（k－2）的顶点是原点，则k____；若顶 点位于x轴上方，则k____；若顶点位于x轴下方， 则k .
5.不画函数y=－x2和y=－x2+1的图象回答下面的问题：
（1）抛物线y=－x2+1经过怎样的平移才能得到抛物 线y=－x2.
（2）函数y=－x2+1，当x 时， y随x的增 大而减小；当x 时，函数y有最大值， 最大值y是 ，其图象与y轴的交点坐标 是 ，与x轴的交点坐标是 .
(－1,0),(1,0)
6.在平面直角坐标系xOy中，函数y=2x2的图象经过 点M（x1，y1），N（x2，y2）两点，若－4＜x1＜ －2，0＜x2＜2，则y1与y2的大小关系是__________.
（3）试说出抛物线y=x2－3的开口方向、对称轴和顶点 坐标.
开口方向向上，对称轴是y轴，顶点坐标（0，－3）.
7.在同一直角坐标系中，一次函数y＝ax＋c和二次 函数y＝ax2＋c的图象大致为(　　)
方法总结：熟记一次函数y＝kx＋b在不同情况下所在的象限，以及熟练掌握二次函数的有关性质(开口方向、对称轴、顶点坐标等)是解决问题的关键．
8.已知 y =(m+1)x 是二次函数,且其图象开口向 上,求m的值和函数解析式
解②得:m1=－2, m2=1
此时,二次函数为: y=2x2.
二次函数y=ax2+c（a≠0)的图象和性质
开口方向由a的符号决定；c决定顶点位置；对称轴是y轴.
增减性结合开口方向和对称轴才能确定.
平移规律：c正向上；c负向下.