初中数学沪科版九年级下册24.2.4 圆的确定教学课件ppt

这是一份初中数学沪科版九年级下册24.2.4 圆的确定教学课件ppt，共24页。PPT课件主要包含了新课导入，无数个，OAOBOC，反证法，反证法的步骤，随堂演练等内容，欢迎下载使用。
经过一点可以作无数条直线
经过两点可以确定一条直线
那么确定一个圆需要几个已知点呢？
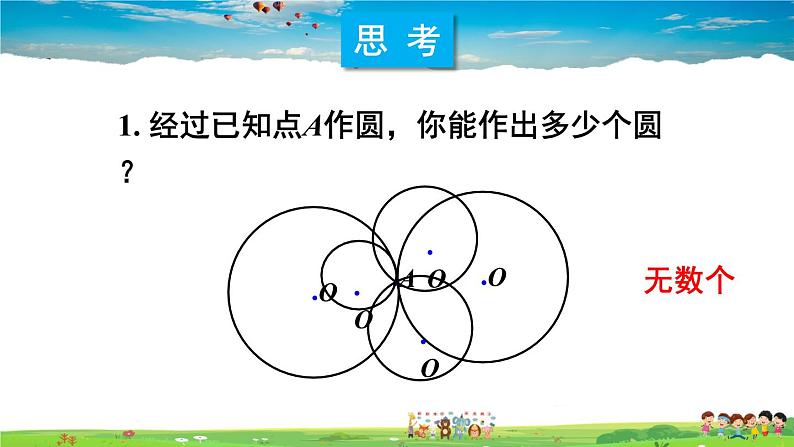
1. 经过已知点A作圆，你能作出多少个圆？
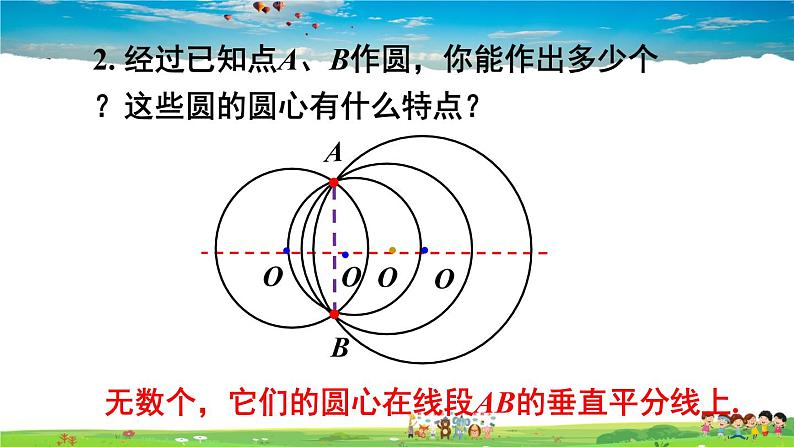
2. 经过已知点A、B作圆，你能作出多少个？这些圆的圆心有什么特点？
无数个，它们的圆心在线段AB的垂直平分线上.
3. 经过同一平面内三个点作圆，情况会怎样呢？
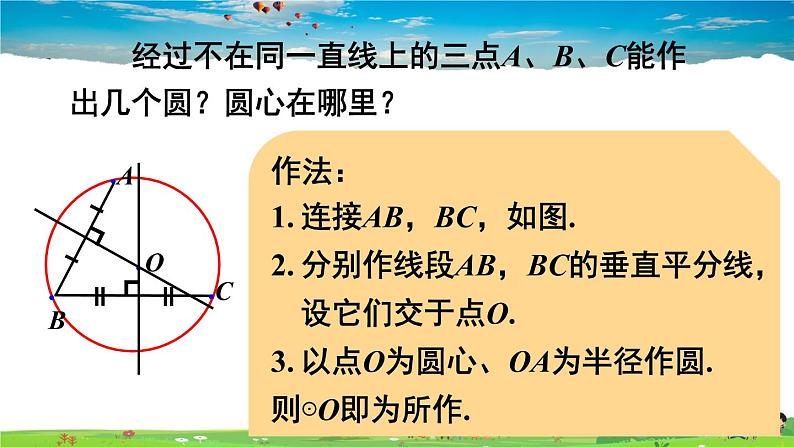
经过不在同一直线上的三点A、B、C能作出几个圆？圆心在哪里？
作法：连接AB，BC，如图.分别作线段AB，BC的垂直平分线，设它们交于点O.以点O为圆心、OA为半径作圆.则⊙O即为所作.
不在同一直线上的三个点确定一个圆.
经过三角形的三个顶点可以作一个圆，这个圆叫做三角形的外接圆，外接圆的圆心叫做这个三角形的外心.
想一想：一个三角形有____ 个外接圆，而一个圆有_____个内接三角形.
三角形的外心到三角形的三个顶点距离相等.
过同一直线上的三点可以作圆吗？
证明：过同一直线上的三点不能作圆.
如图，已知点A、B、C在直线m上.求证：过点A、B、C不能作圆.
证明：假设过同一直线上的三点可以作圆.则该圆的圆心到A、B、C三点的距离都相等，即圆心是线段AB、BC垂直平分线的交点.分别作AB、BC垂直平分线l1、l2.显然l1∥l2，l1与l2无交点，故产生矛盾.所以假设不成立.即过同一直线上的三点不能作圆.
反设：假设命题的结论不成立；
推理：从“反设”出发，逐步推理直至出现与已知条件、定义、基本事实、定理等中的任一个相矛盾的结果；
结论：由矛盾的结果判定“反设”不成立，从而肯定命题的结论成立.
定理 ：两条平行直线被第三条直线所截，同位角相等.
已知：如图直线AB//直线CD，直线EF分别交AB，CD于点O1，O2. 求证：∠EO1B=∠EO2D.
证明：假设∠EO1B ≠∠EO2D，过O1作直线A′B′，使∠EO1B ′ =∠EO2D.
根据“同位角相等，两直线平行”，得A′B′//CD.
这样过点O1就有两条直线AB， A′B′平行于直线CD，这与“过直线外一点有且只有一条直线与这条直线平行”相矛盾.
即∠EO1B ≠∠EO2D的假设不成立，所以∠EO1B=∠EO2D.
1. 判断下列说法是否正确：(1) 任意的一个三角形一定有一个外接圆.( )(2) 任意一个圆有且只有一个内接三角形.( )(3) 经过三点一定可以确定一个圆.( )(4) 三角形的外心到三角形各顶点的距离相等.( )
2. 若一个三角形的外心在一边上，则此三角形的形状为( ) A．锐角三角形 B．直角三角形 C．钝角三角形 D．等腰三角形
3.某地出土一明代残破圆形瓷盘，如图所示．为复制该瓷盘要确定其圆心和半径,请在图中用直尺和圆规画出瓷盘的圆心．
解：(1)在圆形瓷盘的边缘选A、B、C三点；
(2)连接AB、BC；
(3)分别作出AB、BC的垂直平分线；
(4)两垂直平分线的交点就是瓷盘的圆心.
4. 用反证法证明：等腰三角形的底角一定是锐角.
分析：由题目分析，“一定是锐角”的反面就是“不是锐角”，即是直角或钝角，因此应分两种情况讨论.
已知：在△ABC中，AB=AC，求证：∠B,∠C一定是锐角.
证明：假设∠B,∠C不是锐角，则∠B,∠C是直角 或钝角.（1）若∠B,∠C是直角，即∠B=∠C=90°， 故∠A+∠B+∠C >180°, 这与三角形的内角和定理矛盾， 所以∠B,∠C不是直角.
（2）若∠B,∠C是钝角，即∠B=∠C >90°， 故∠A+∠B+∠C >180°, 这与三角形的内角和定理矛盾， 所以∠B,∠C不是钝角. 综上所述，∠B,∠C不是直角也不是钝角， 即∠B,∠C是锐角， 所以等腰三角形的底角一定是锐角.