数学九年级下册第24章 圆24.3 圆周角24.3.1 圆周角定理教学ppt课件

这是一份数学九年级下册第24章 圆24.3 圆周角24.3.1 圆周角定理教学ppt课件，共19页。PPT课件主要包含了新课导入，第一种情况，第二种情况，第三种情况，对应训练，∠BDC∠CAE，推论1，推论2，解连接BC，则∠ACB90°等内容，欢迎下载使用。

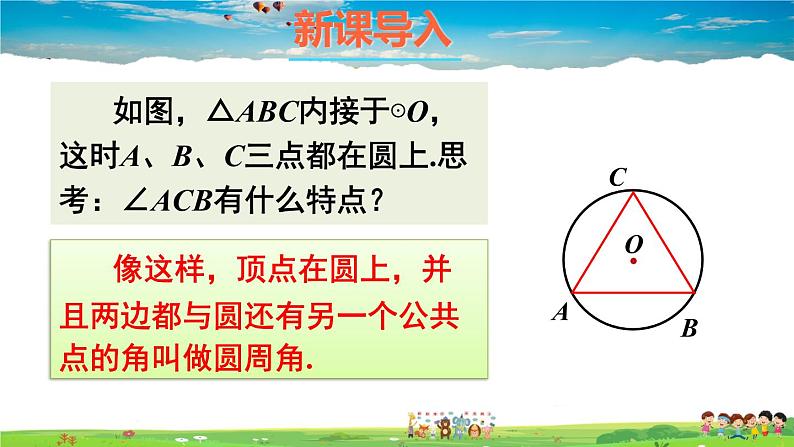
如图，△ABC内接于⊙O，这时A、B、C三点都在圆上.思考：∠ACB有什么特点？
像这样，顶点在圆上，并且两边都与圆还有另一个公共点的角叫做圆周角.
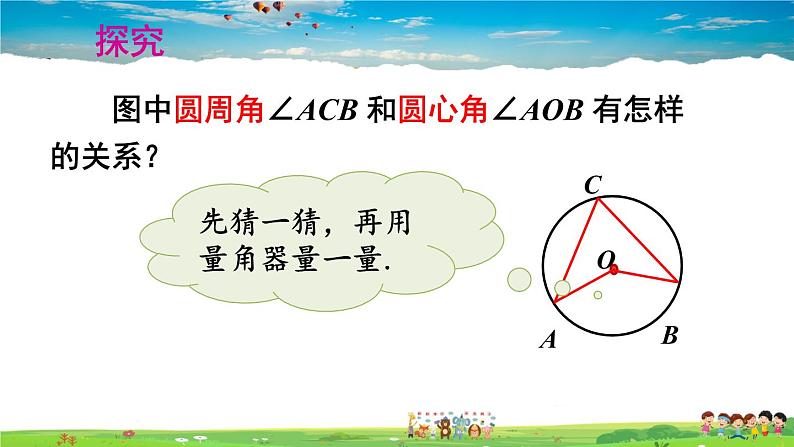
　　图中圆周角∠ACB 和圆心角∠AOB 有怎样的关系？
先猜一猜，再用量角器量一量.
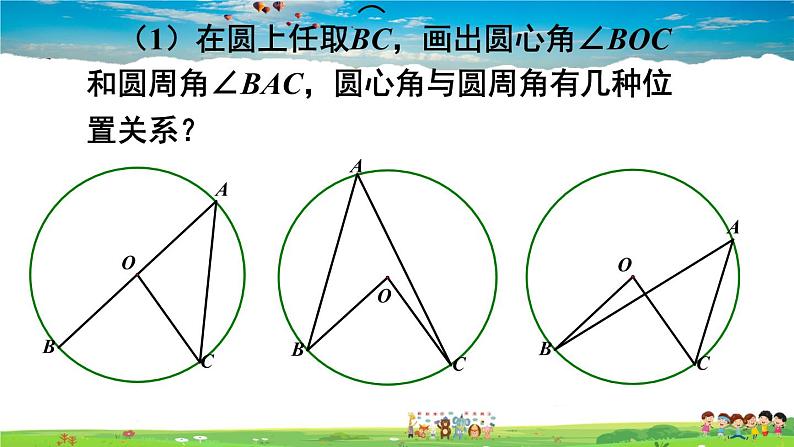
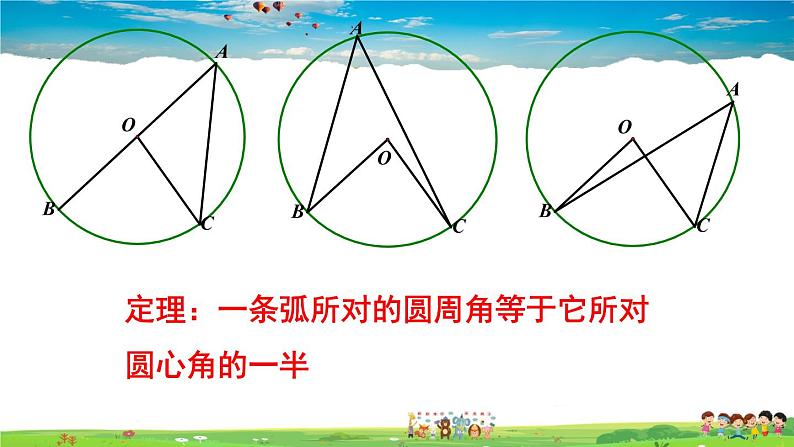
　　（1）在圆上任取BC，画出圆心角∠BOC 和圆周角∠BAC，圆心角与圆周角有几种位置关系？
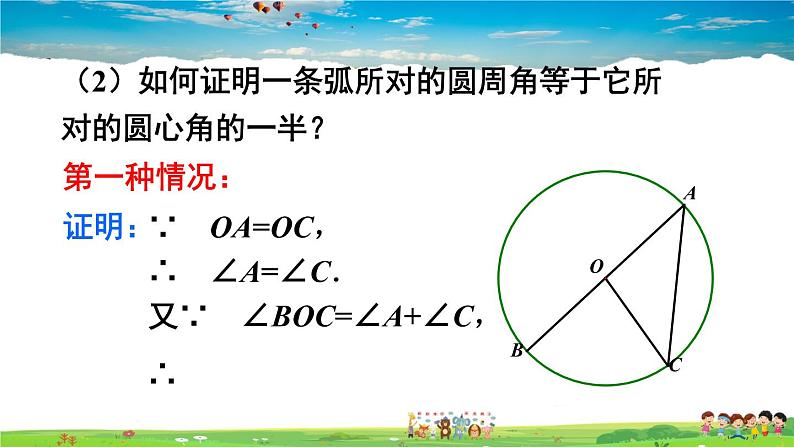
（2）如何证明一条弧所对的圆周角等于它所对的圆心角的一半？
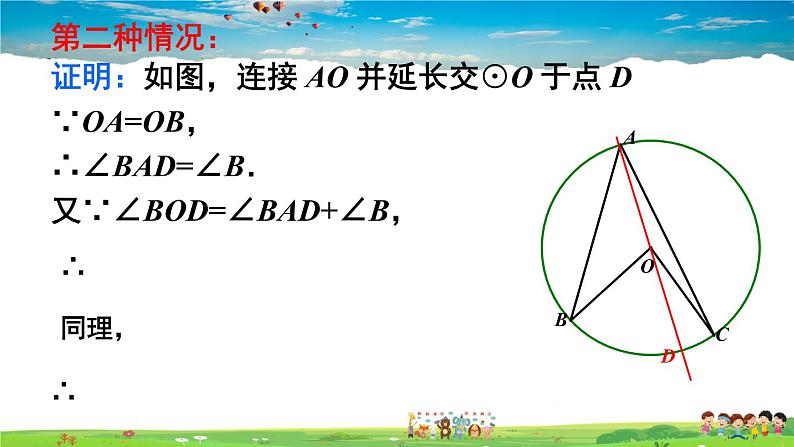
证明：如图，连接 AO 并延长交⊙O 于点 D∵OA=OB，∴∠BAD=∠B．又∵∠BOD=∠BAD+∠B，
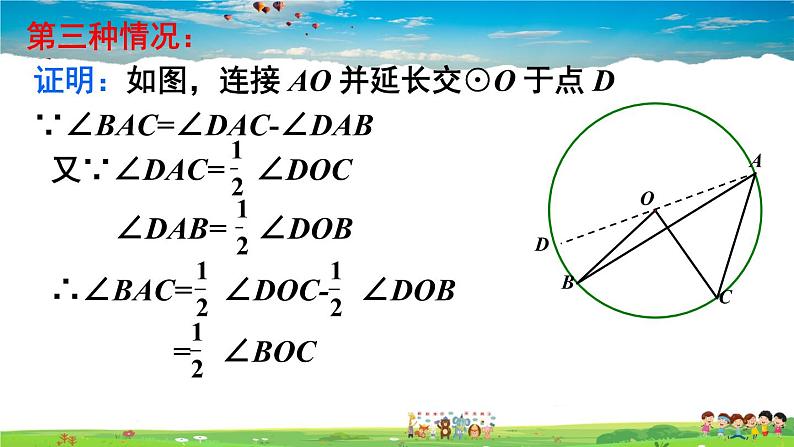
证明：如图，连接 AO 并延长交⊙O 于点 D∵∠BAC=∠DAC-∠DAB
定理：一条弧所对的圆周角等于它所对圆心角的一半
如图，⊙O是△ABC的外接圆，∠OCB＝50°，则∠A等于( ) A.40° B.50° C.60° D.70°
根据圆周角定理可知，
同弧所对的圆周角相等．
如图，作出两弧所对应的圆心角.根据圆周角定理可知，
等弧所对的圆周角相等．
在同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等.
半圆或直径所对的圆周角是直角；90°的圆周角所对的弦是直径.
例1 如图AB为⊙O的直径，弦CD交AB于点P，∠ACD=60°，∠ADC=70°，求∠APC的度数.
∠DCB=∠ACB-∠ACD =90°-60°=30°.又∵∠BAD=∠DCB=30°， ∴∠APC=∠BAD+∠ADC =30°+70 =100°
1.下列四个图中，∠x是圆周角的是( )
2.如图，⊙O中，弦AB、CD相交于E点，且∠A=40°，∠AED=75°，则∠B=( )A.15° B.40° C.5° D.35°
3.如图，⊙O中，弦AD平行于弦BC，∠AOC=78°，求∠DAB的度数．解：∵AD∥BC， ∴∠DAB=∠B. 又∵∠B= ∠AOC=39°. ∴∠DAB=39°.
顶点在圆上，并且两边都和圆相交的角.
一条弧所对的圆周角等于它所对的圆心角的一半．
①同弧或等弧所对的圆周角相等．
②半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径.