沪科版九年级下册24.7.1 弧长与扇形面积教学课件ppt

这是一份沪科版九年级下册24.7.1 弧长与扇形面积教学课件ppt，共19页。PPT课件主要包含了新课导入，新课推进，C2πR，弧长公式，什么是扇形，圆心角，如何求扇形的面积，SπR2，扇形面积公式，弧长与扇形面积的关系等内容，欢迎下载使用。

问题：怎样求一段弧的长度呢？
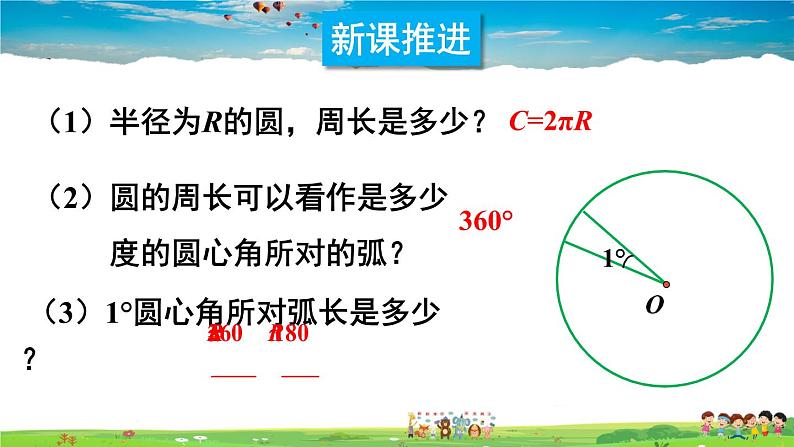
（1）半径为R的圆，周长是多少？
（3）1°圆心角所对弧长是多少？
（2）圆的周长可以看作是多少 度的圆心角所对的弧？
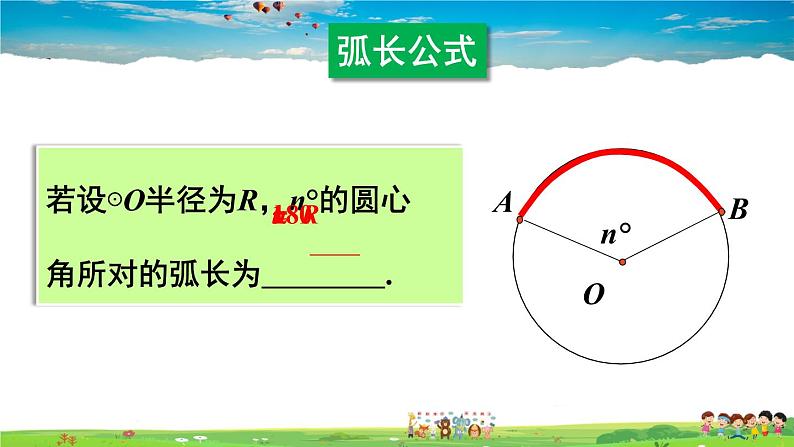
若设⊙O半径为R，n°的圆心角所对的弧长为 .
（1）半径为R，140°圆心角所对的弧长是多少？
（2）已知半径为3，则弧长为π的弧所对的圆心角为_______.
例1 一滑轮装置如图，滑轮的半径R=10cm，当重物上升15.7cm时，问滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度？（假设绳索与滑轮之间没有滑动，π取3.14）
解 设半径OA绕轴心O按逆时针方向旋转n°，则
解方程，得 n≈90.答：旋转的角度约为90°.
如下图，由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形.
在半径为R 的圆中，n°的圆心角所对的扇形面积计算公式为
扇形的面积与扇形所在的圆的半径和弧所对的圆心角的度数有关系.
比较扇形面积(S)公式和弧长(l)公式，你能用弧长来表示扇形的面积吗?
1. 已知扇形的圆心角为120°，半径为2，则这个扇形的面积为多少？
2. 已知扇形的半径为3cm，扇形的弧长为πcm，则该扇形的面积是______cm2.
1.已知扇形的圆心角为120°，半径为6,则扇形的弧长是 °的圆心角所对的弧长是2.5πcm，则此弧所在的圆半径是 cm.3.一个扇形的弧长为20πcm，面积是240πcm2，则扇形的圆心角是 .
4. 如图是一段弯形管道，其中,∠O=∠O′=90°，中心线的两条圆弧半径都为1000mm,求图中管道的展直长度. (π取3.142)
解：答：图中管道的展直长度约为6142mm.
5. 草坪上的自动喷水装置能旋转220°，如果它的喷射半径是20m，求它能喷灌的草坪的面积.
解： 答：它能喷灌的草坪的面积为 πm2.
6.如图，扇形纸扇完全打开后，外侧两竹条AB、AC夹角为120°，AB的长为30cm，贴纸部分BD的长为20cm，求贴纸部分的面积.