


沪科版九年级下册第24章 圆综合与测试教学ppt课件
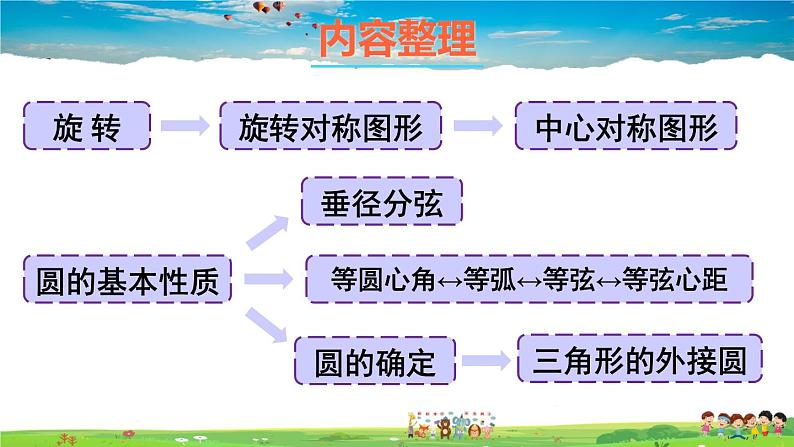
展开等圆心角↔等弧↔等弦↔等弦心距
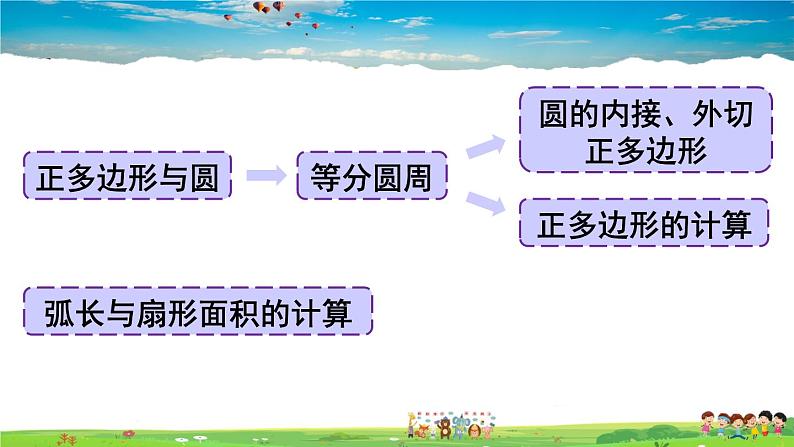
圆的内接、外切正多边形
在平面内,_____________________________________________________________,叫做旋转.旋转是由________,________和________所确定.
一个图形绕着一个定点,旋转一定
的角度,得到另一个图形的变换
在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图_______,这样的图形叫做旋转对称图形,这个定点就是旋转中心.
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心.
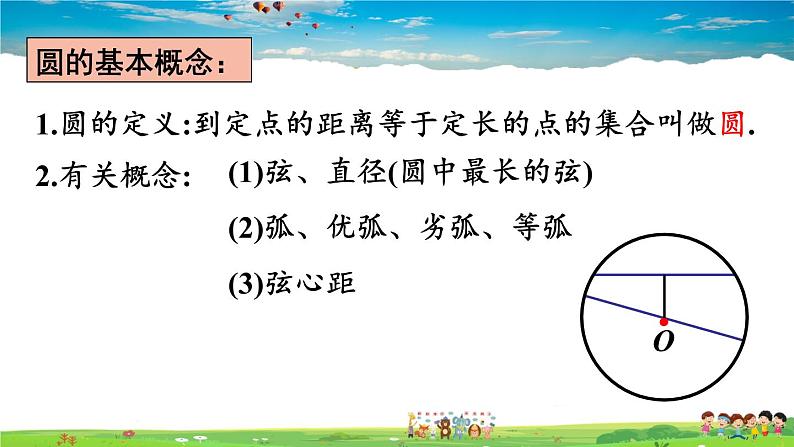
1.圆的定义:到定点的距离等于定长的点的集合叫做圆.
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
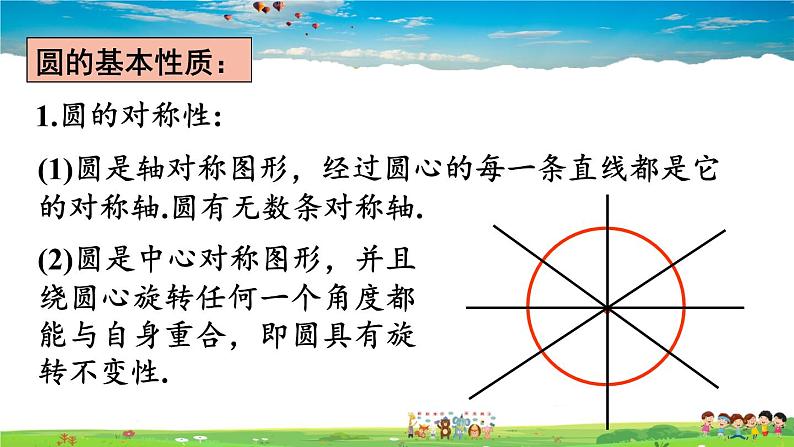
(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.
(2)圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,即圆具有旋转不变性.
垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
∵CD是圆O的直径,CD⊥AB
3.同圆或等圆中圆心角、弧、弦之间的关系:
(1)在同圆或等圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等.
∵ ∠COD =∠AOB
(2)在圆中,如果弧相等,那么它所对的圆心角相等,所对的弦相等.
(3)在一个圆中,如果弦相等,那么它所对的弧相等,所对的圆心角相等.
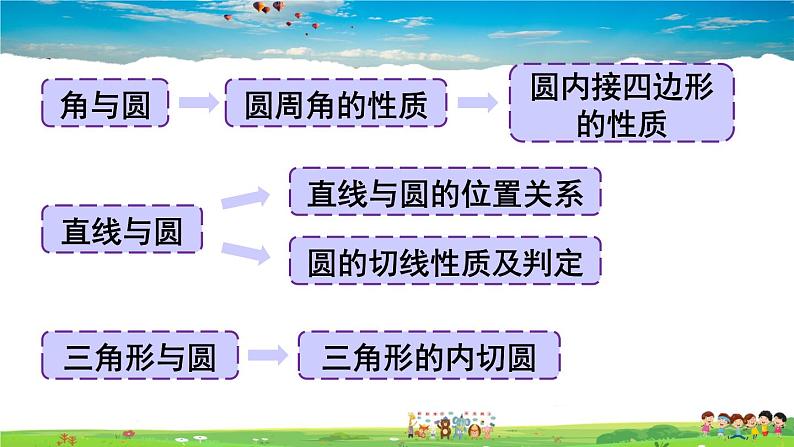
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
性质1:在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.
性质2:在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧相等.
∵∠ADB与∠AEB 、∠ACB 是同弧所对的圆周角
∴∠ADB=∠AEB =∠ACB
性质3:半圆或直径所对的圆周角都相等,都等于90°(直角).
性质4:90°的圆周角所对的弦是圆的直径.
如果规定点与圆心的距离为d,圆的半径为r,则d与r的大小关系为:
2.直线和圆的位置关系:
一条直线与一个圆没有公共点,叫做直线与这个圆相离.
一条直线与一个圆只有一个公共点,叫做直线与这个圆相切.
一条直线与一个圆有两个公共点,叫做直线与这个圆相交.
直线与圆位置关系的识别:
设圆的半径为r,圆心到直线的距离为d,则:
(1)当直线与圆相离时d>r;
(2)当直线与圆相切时d=r;
(3)当直线与圆相交时d<r.
1.与圆有一个公共点的直线.
2.圆心到直线的距离等于圆的半径的直线是圆的切线.
3.经过半径的外端且垂直于这条半径的直线是圆的切线.
∵OA是半径,OA⊥ l
∴直线l是⊙O的切线.
(1)圆的切线垂直于经过切点的半径.
(2)经过圆心垂直于切线的直线必经过切点.
(3)经过切点垂直于切线的直线必经过圆心.
∵直线l是⊙O的切线,切点为A
从圆外一点引圆的两条切线,它们的切线长相等;这点与圆心的连线平分这两条切线的夹角.
∵PA、PB为⊙O的切线
∠APO = ∠BPO
3.圆与圆的位置关系:
三角形的外接圆与内切圆:
三角形的外心就是三角形各边垂直平分线的交点.
三角形的内心就是三角形各角平分线的交点.
不在同一直线上的三点确定一个圆.
等边三角形的外心与内心重合.
内切圆半径与外接圆半径的比是1:2.
1.过一点的圆有________________个.2.过两点的圆有________________个,这些圆的圆心的都在_______________________________上.3.过三点的圆有______________个.4.如何作过不在同一直线上的三点的圆(或三角形的外接圆、找外心、破镜重圆、到三个村庄距离相等).5.锐角三角形的外心在三角形____,直角三角形的外心在三角形_______________,钝角三角形的外心在三角形____.
连结着两点的线段的垂直平分线
经过三角形的三个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,三角形叫做圆的内接三角形.
问题1:如何作三角形的外接圆?如何找三角形的外心?问题2:三角形的外心一定在三角形内吗?
正多边形的中心:该正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径.
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:中心到正多边形的一边的距离.
(1)有关概念(2)常用的方法(3)正多边形的作图
弧长与扇形面积的计算:
若设⊙O半径为R,n°的圆心角所对的弧长为 .
圆锥的侧面积=扇形的面积
1.如图,在⊙O中,弦AB,CD相交于点P,∠A=40°,∠APD=75°,则∠B等于( )A.15° B.40° C.75° D.35°
2.如图,PA,PB分别切⊙O于点A,B,∠P=70°,则∠C=( )A.70° B.55° C.110° D.140°
3.以半径为1的圆内接正三角形、正方形、正六边形的边心距为三边作三角形,则( )A. 不能构成三角形 B. 这个三角形是等腰三角形C. 这个三角形是直角三角形D. 这个三角形是钝角三角形
4.一个圆锥的侧面积是底面积的 倍,则圆锥侧面展开图的扇形的圆心角是( )A.120° B.180° C.240° D.300°
5.如图所示,P是⊙O外一点,PA、PB分别和⊙O切于点A、B,点C是AB上任意一点,过点C作⊙O的切线分别交PA、PB于点D、E,若△PDE的周长为12,则PA的长为 .
6.如图,AC=CB,D,E分别是半径OA,OB的中点.求证:CD=CE.证明:连接OC.∵AC=CB,∴∠COD=∠COE.∵D、E分别是半径OA、OB的中点,∴OD=OE= OA= OB.又OC=OC,∴△COD≌△COE.∴CD=CE.
7.在直径为650mm的圆柱形油槽内装入一些油以后,截面如图所示,若油面宽AB=600mm,求油的最大深度. 解:过O作OD⊥AB,交AB于点C,交⊙O于点D.则AC= AB=300mm.连接OA.设CD=xmm,则OC=(325-x)mm.在Rt△AOC中,OC2+AC2=OA2,即(325-x)2+3002=3252.解得x=200.即CD=200mm.答:油的最大深度为200mm.
8.如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,求证:AC平分∠DAB.证明:连接OC.∵OA=OC,∴∠OAC=∠OCA.又∵DC是⊙O的切线, ∴OC⊥CD.又AD⊥CD,∴AD∥CO.∴∠DAC=∠OCA,∴∠DAC=∠OAC.∴AC平分∠DAB.
9.如图,在等腰三角形ABC中,AB=AC,以AC为直径作⊙O,与BC交于点E,过点E作ED⊥AB,垂足为D.求证:DE为⊙O的切线.证明:连接OE,AE.∵AC是⊙O的直径,∴∠AEC=90°.又∵AB=AC, ∴∠B=∠C.∵∠B=90°-∠DAE=∠DEA.∴∠DEA=∠C,又∵OE=OA, ∴∠EAO=∠AEO∴∠DEO=∠DEA+∠AEO=∠C+∠EAO=90°.又DE过点E,∴DE为⊙O的切线.
1.通过这节课的学习,你有哪些收获?2.你还存在哪些疑问,与同伴交流。
初中数学沪科版九年级下册第24章 圆综合与测试复习ppt课件: 这是一份初中数学沪科版九年级下册第24章 圆综合与测试复习ppt课件,共15页。
北师大版九年级下册第三章 圆综合与测试教学ppt课件: 这是一份北师大版九年级下册第三章 圆综合与测试教学ppt课件,共14页。PPT课件主要包含了cm或2cm,2π+50等内容,欢迎下载使用。
华师大版九年级下册第27章 圆综合与测试教学课件ppt: 这是一份华师大版九年级下册第27章 圆综合与测试教学课件ppt,共21页。PPT课件主要包含了等腰直角等内容,欢迎下载使用。













