人教A版 (2019)必修 第一册4.2 指数函数课时训练

4.2.2　指数函数的图象和性质

基础过关练

题组一　指数函数的图象特征

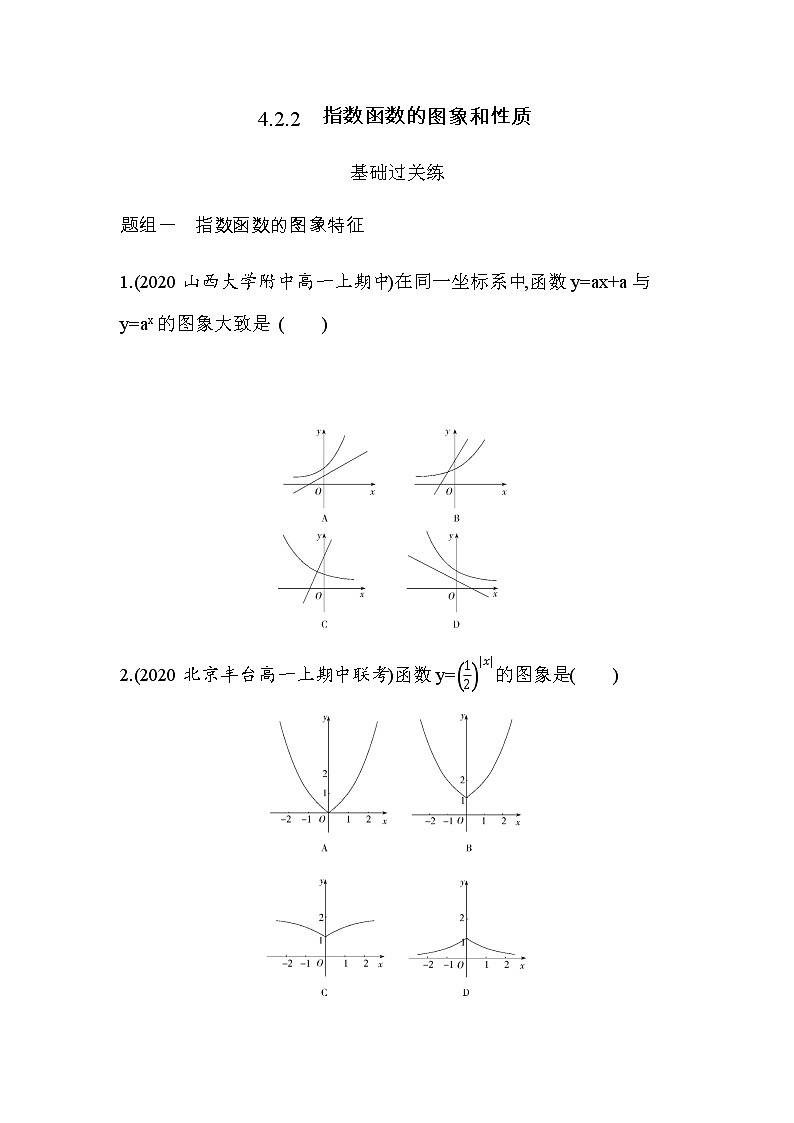
1.(2020山西大学附中高一上期中)在同一坐标系中,函数y=ax+a与y=ax的图象大致是 (　　)

2.(2020北京丰台高一上期中联考)函数y=的图象是(　　)

3.(2020湖南衡阳八中高一上期中)设a,b,c,d均大于0,且均不等于1,y=ax ,y=bx ,y=cx ,y=dx在同一坐标系中的图象如图,则a,b,c,d的大小顺序为(　　)

A.a<b<c<d B.a<b<d<c

C.b<a<d<c D.b<a<c<d

4.(2020山西长治二中高一上期中)函数f(x)=ax-2+1(a>0,且a≠1)的图象恒过定点(　　)

A.(2,2) B.(2,1)

C.(3,1) D.(3,2)

5.已知函数f(x)=ax,g(x)=(a>0,且a≠1), f(-1)=.

(1)求f(x)和g(x)的函数解析式;

(2)在同一坐标系中画出函数f(x)和g(x)的图象;

(3)若f(x)<g(x),请直接写出x的取值范围.

题组二　指数函数的单调性及其应用

6.方程4x-3×2x+2=0的解构成的集合为(　　)

A.{0} B.{1} C.{0,1} D.{1,2}

7.(2020山东师大附中高一上第一次学分认定考试)设y1=40.9,y2=80.61,y3=,则(　　)

A.y1>y2>y3 B.y2>y1>y3

C.y1>y3>y2 D.y3>y2>y1

8.(2020广东湛江一中高一上第一次大考)若f(x)=-x2+2ax与g(x)=(a+1)1-x在区间[1,2]上都是减函数,则a的取值范围是(　　)

A. B.

C.[0,1] D.(0,1]

9.若不等式≤的解集是函数y=2x的定义域,则函数y=2x的值域是(　　)

A. B.

C. D.[2,+∞)

10.(2020广东珠海高一上期末) 已知函数f(x)满足f(x+1)的定义域是[0,31),则f(2x)的定义域是(　　)

A.[1,32) B.[-1,30)

C.[0,5) D.(-∞,30]

11.(2020甘肃兰州一中高一月考)函数y=的单调递增区间为　　　　. 

12.(2020浙江嘉兴一中高一上期中)已知集合A=,B={x|x2-11x+18<0}.

(1)求∁R(A∩B);

(2)已知C={x|a<x<a+1},若C⊆B,求实数a的取值集合.

题组三　指数函数性质的综合应用

13.(2020浙江温州十五校联合体高一上期中联考)函数f(x)=的定义域为(　　)

A.[-1,0)∪(0,+∞) B.(-1,+∞)

C.[-1,+∞) D.(0,+∞)

14.已知函数f(x)=3x-,则f(x)是(　　)

A.奇函数,且在R上是增函数

B.偶函数,且在R上是增函数

C.奇函数,且在R上是减函数

D.偶函数,且在R上是减函数

15.(2019湖南醴陵一中高一上期中)函数f(x)=+a是奇函数,则实数a的值是(　　)

A.0  B.  C.- D.1

16.已知a>0,且a≠1,若函数f(x)=2ax-4在区间[-1,2]上的最大值为10,则a=　　　　. 

17.(2020浙江杭州高级中学高一上期末)函数y=的单调递增区间为　　　　;奇偶性为　　　　(填“奇函数”“偶函数”或“非奇非偶函数”). 

18.(2020山东泰安一中高一上期中)已知函数f(x)=a+.

(1)求函数f(x)的定义域;

(2)若f(x)为奇函数,求a的值,并求f(x)的值域.

能力提升练

题组一　指数函数的图象特征

1.(2020福建厦外高一上期中,)已知函数f(x)=(x-a)(x-b)(其中a>b)的图象如图所示,则函数g(x)=ax+b的图象是(　　)

2.(2020陕西西安中学高一上期中,)已知实数a,b满足等式2 019a=2 020b,下列五个关系式:①0<b<a;②a<b<0;③0<a<b;④b<a<0;⑤a=b.其中不可能成立的关系式有(　　)　　　　　 　　　　　 　　　　　

A.1个 B.2个 C.3个 D.4个

3.(2020河北唐山一中高一上期中,)若函数y=+m的图象与x轴有公共点,则m的取值范围是　　　. 

题组二　指数函数的单调性及其应用

4.(2020湖南长郡中学高一上模块检测,)已知a=,b=20.3,c=0.30.2,则a,b,c三者的大小关系是(　　)

A.b>c>a B.b>a>c C.a>b>c D.c>b>a

5.()函数f(x)=-a2x-1+5ax-8(a>0,且a≠1)在[2,+∞)上单调递减,则实数a的取值范围为(　易错　)

A.(0,1)∪

B.∪(1,+∞)

C.(0,1)∪

D.

6.()若函数f(x)=的定义域为R,则实数a的取值范围是　　　　.  

7.(2020黑龙江大庆实验中学高一上月考,)已知函数f(x)=bax(其中a,b为常数,a>0,且a≠1)的图象经过A(1,6),B(2,18)两点.若不等式+-m≥0在x∈(-∞,1]上恒成立,则实数m的最大值为　　　. 

8.(2020福建福州八县(市)一中高一上期末联考,)已知定义在R上的偶函数f(x)满足:当x≥0时, f(x)=2x+, f(1)=.

(1)求实数a的值;

(2)用定义法证明f(x)在(0,+∞)上是增函数;

(3)求函数f(x)在[-1,2]上的值域.

题组三　指数函数性质的综合应用

9.(2020安徽安庆高一上期末,)某数学课外兴趣小组对函数f(x)=2|x-1|的图象与性质进行了探究,得到下列四条结论:①函数f(x)的值域为(0,+∞);②函数f(x)在区间[0,+∞)上单调递增;③函数f(x)的图象关于直线x=1对称;④函数f(x)的图象与直线y=-a2(a∈R)不可能有交点.

则其中正确结论的个数为(深度解析)

A.1 B.2 C.3 D.4

10.(2020浙江温州十五校联合体高一上期中联考,)已知a>0,设函数f(x)=(x∈[-a,a])的最大值为M,最小值为N,那么M+N=(　　)

A.2 025 B.2 022 C.2 020 D.2 019

11.(2020浙江浙北G2高一上期中联考,)已知实数a>0,定义域为R的函数f(x)=+是偶函数.

(1)求实数a的值;

(2)判断函数f(x)在(0,+∞)上的单调性并用定义证明;

(3)是否存在实数m,使得对任意的t∈R,不等式f(t-2)<f(2t-m)恒成立?若存在,求出m的取值范围;若不存在,请说明理由.

答案全解全析

基础过关练

1.B　函数y=ax+a的图象经过(-1,0)和(0,a)两点,选项D错误;在图A中,由指数函数y=ax的图象得a>1,由y=ax+a的图象得0<a<1,选项A错误;在图B中,由指数函数y=ax的图象得a>1,由y=ax+a的图象得a>1,选项B正确;在图C中,由指数函数y=ax的图象得0<a<1,由y=ax+a的图象得a>1,选项C错误.故选B.

2.D　y==

因此,当x≥0时,y=的图象与y=的图象相同;当x<0时,y=的图象与y=2x的图象相同,故选D.

3.C　作出直线x=1,如图所示.

直线x=1与四个函数图象的交点从下到上依次为(1,b),(1,a),(1,d),(1,c),因此a,b,c,d的大小顺序是b<a<d<c,故选C.

4.A　∵a0=1,∴令x-2=0,得y=a0+1=2,

∴x=2时,y=2,

因此函数f(x)的图象恒过定点(2,2),故选A.

5.解析　(1)因为f(-1)=a-1==,所以a=2,

所以f(x)=2x,g(x)=.

(2)在同一坐标系中画出函数f(x)和g(x)的图象如图所示:

(3)由图象知,当f(x)<g(x)时,x的取值范围是{x|x<0}.

6.C　令2x=t,则4x=(2x)2=t2,

原方程可化为t2-3t+2=0,解得t=1或t=2.

当t=1时,2x=1=20,解得x=0,

当t=2时,2x=2=21,解得x=1.

因此原方程的解构成的集合为{0,1}.

故选C.

7.B　由题意知,y1=40.9=22×0.9=21.8,y2=80.61=23×0.61=21.83,y3==21.5,∵y=2x在R上是增函数,∴y2>y1>y3.故选B.

8.D　由f(x)=-x2+2ax=-(x-a)2+a2在区间[1,2]上是减函数得a≤1;由g(x)=(a+1=在区间[1,2]上是减函数得0<<1,因此a+1>1,解得a>0.因此a的取值范围是(0,1],故选D.

9.B　由≤得≤2-2x+4,即x2+1≤-2x+4,解得-3≤x≤1,∴函数y=2x的定义域为[-3,1].由于函数y=2x在R上单调递增,故当x=-3时取得最小值,当x=1时取得最大值2,所以函数的值域为.故选B.

10.C　∵f(x+1)的定义域是[0,31),即0≤x<31,∴1≤x+1<32,∴f(x)的定义域是[1,32),

∴f(2x)有意义必须满足20=1≤2x<32=25,∴0≤x<5.

11.答案　[-1,+∞)

解析　设t=8-2x-x2,则y=,易知y=在R上单调递减,

又知t=8-2x-x2在(-∞,-1]上单调递增,在[-1,+∞)上单调递减,

所以由y=与t=8-2x-x2复合而成的函数y=的单调递增区间为[-1,+∞).

12.解析　由≤2x-4<4得2-1≤2x-4<22,

∴-1≤x-4<2,即3≤x<6,∴A=[3,6).

由x2-11x+18<0得2<x<9,∴B=(2,9).

(1)∵A=[3,6),B=(2,9),

∴A∩B=[3,6),

∴∁R(A∩B)=(-∞,3)∪[6,+∞).

(2)由C⊆B得

解得2≤a≤8,

故实数a的取值集合为{a|2≤a≤8}.

13.A　依题意得即

故函数f(x)的定义域为[-1,0)∪(0,+∞),故选A.

14.A　由题知x∈R,且f(-x)=3-x-=-3x=-f(x),所以f(x)是奇函数;又y=3x是增函数,且y=是减函数,所以f(x)=3x-是R上的增函数,故选A.

15.C　函数f(x)=+a的定义域为R,且f(x)是奇函数,因此f(0)=0,即+a=0,解得a=-.

此时f(x)=-=符合题意,故选C.

16.答案　或

解析　若a>1,则函数y=ax在区间[-1,2]上是单调递增的,

当x=2时, f(x)取得最大值,则f(2)=2a2-4=10,即a2=7,又a>1,所以a=.

若0<a<1,则函数y=ax在区间[-1,2]上是单调递减的,

当x=-1时, f(x)取得最大值,则f(-1)=2a-1-4=10,所以a=.

综上所述,a的值为或.

17.答案　[0,+∞);偶函数

解析　设u=-|x|+1,则y=.

易知u=-|x|+1的单调递减区间为[0,+∞),y=是减函数,

∴y=的单调递增区间为[0,+∞).

∵f(-x)===f(x),

∴f(x)是偶函数.

18.解析　(1)由2x-1≠0,可得x≠0,

∴函数f(x)的定义域为{x|x≠0}.

(2)∵f(x)为奇函数,∴f(-x)=-f(x).

又∵f(-x)=a+=a+=a-=(a-2)-,

-f(x)=-a-,

∴a-2=-a,解得a=1.

因此f(x)=1+.

∴当x>0时,2x-1>0,f(x)>1;

当x<0时,-1<2x-1<0,f(x)<-1.

∴f(x)的值域为(-∞,-1)∪(1,+∞).

能力提升练

1.A　由函数f(x)的图象知,b<-1<0<a<1.

∴g(x)=ax+b的图象是单调递减的.

又g(0)=a0+b=1+b<0,∴图象与y轴交于负半轴,故选A.

2.B　在同一平面直角坐标系中作出y=2 019x与y=2 020x的图象如图所示.

设2 020b=2 019a=t,

当t>1时,0<b<a,①正确;

当t=1时,a=b=0,⑤正确;

当0<t<1时,a<b<0,②正确,③④不成立.

故选B.

3.答案　 [-1,0)

解析　作出函数g(x)==的图象如图所示.

由图象可知0<g(x)≤1,则m<g(x)+m≤1+m,即m<f(x)≤1+m,

要使函数y=+m的图象与x轴有公共点,则解得-1≤m<0.

故答案为[-1,0).

4.A　a==0.30.5.

∵f(x)=0.3x在R上单调递减,

∴0.30.5<0.30.2<0.30⇒a<c<1.

又b=20.3>20=1,∴a<c<b,故选A.

5.A　设y=f(x)=-·a2x+5ax-8,令ax=u(u>0),

则y=-u2+5u-8=-+-8(u>0).

∴y=-u2+5u-8在上单调递增,在上单调递减.

①当0<a<1时,u=ax是减函数,

∵x≥2,∴0<u≤a2<,

此时y=-u2+5u-8是增函数,

从而f(x)是减函数,符合题意.

②当a>1时,u=ax是增函数,

∵x≥2,∴u≥a2,

由f(x)在[2,+∞)上单调递减,得a2≥,

又a>0,∴a≥,

即当a≥时,f(x)是减函数.

综上所述,实数a的取值范围是(0,1)∪,

故选A.

易错警示　解决与指数函数有关的复合函数的单调性问题时,一要注意底数的取值对单调性的影响,必要时进行分类讨论;二要注意中间变量的取值范围.

6.答案　[-1,0]

解析　依题意得-1≥0恒成立,即x2+2ax-a≥0恒成立.

∴Δ=4a2+4a≤0,解得-1≤a≤0,

故实数a的取值范围是[-1,0].

7.答案　

解析　由已知可得解得

则不等式+-m≥0在x∈(-∞,1]上恒成立,设g(x)=+-m,

显然函数g(x)=+-m在(-∞,1]上单调递减,

∴g(x)≥g(1)=+-m=-m,

故-m≥0,即m≤,

∴实数m的最大值为.

8.解析　(1)由题意得f(1)=2+=,

∴a=1.

(2)证明:由(1)知a=1,∴f(x)=2x+,任取x1,x2∈(0,+∞),且x1<x2,则

f(x1)-f(x2)=-=(-)+=(-)·.

∵0<x1<x2,∴1<<,>1,

∴f(x1)-f(x2)<0,∴f(x1)<f(x2),

∴f(x)在(0,+∞)上是增函数.

(3)易得f(0)=2, f(2)=, f(-1)=, f(x)在[-1,0]上为减函数,在[0,2]上为增函数,

∴f(x)的值域为.

9.B　函数f(x)的值域为[1,+∞),①错误;函数f(x)在区间[0,1)上单调递减,在[1,+∞)上单调递增,②错误;函数f(x)的图象关于直线x=1对称,③正确;因为y=-a2≤0,所以函数f(x)的图象与直线y=-a2(a∈R)不可能有交点,④正确.正确结论的个数为2,故选B.

解题模板　研究指数型复合函数的性质,借助图象是常见的手段,画出简图很多问题可迎刃而解.

10.B　f(x)==2 019-,

∴f(-x)=2 019-=2 019-.

因此f(x)+f(-x)

=4 038-2 016

=4 038-2 016=2 022.

又f(x)在[-a,a]上是增函数,

∴M+N=f(a)+f(-a)=2 022,故选B.

11.解析　(1)定义域为R的函数f(x)=+是偶函数,则f(-x)=f(x)恒成立,即+=+,故(3x-3-x)=0恒成立.

因为3x-3-x不可能恒为0,所以当-a=0时,f(-x)=f(x)恒成立,而a>0,所以a=1.

(2)函数f(x)=3x+在(0,+∞)上单调递增,证明如下:

设任取x1,x2∈(0,+∞),且x1<x2,则

f(x1)-f(x2)=-=(-)+=(-)+

=.

因为0<x1<x2,所以<,>1,>1,

所以<0,

即f(x1)-f(x2)<0,即f(x1)<f(x2),

故函数f(x)=3x+在(0,+∞)上单调递增.

(3)不存在.理由如下:由(2)知函数f(x)在(0,+∞)上单调递增,而函数f(x)是偶函数,则函数f(x)在(-∞,0)上单调递减.若存在实数m,使得对任意的t∈R,不等式f(t-2)<f(2t-m)恒成立,则|t-2|<|2t-m|恒成立,即(t-2)2<(2t-m)2,即3t2-(4m-4)t+m2-4>0对任意的t∈R恒成立,则Δ=[-(4m-4)]2-12(m2-4)<0,得到(m-4)2<0,故m∈⌀,所以不存在.