





华师大版八年级下册第17章 函数及其图象17.1 变量与函数教案配套课件ppt
展开1.理解自变量应符合实际意义.2.会求函数的值,并确定自变量的取值范围.(难点)
请用含自变量的式子表示下列问题中的函数关系:(1)汽车以60 km/h 的速度匀速行驶,行驶的时间为 t(单位:h),行驶的路程为 s(单位:km);(2)多边形的边数为 n,内角和的度数为 y.
问题(1)中,t 取-2 有实际意义吗? 问题(2)中,n 取2 有意义吗?
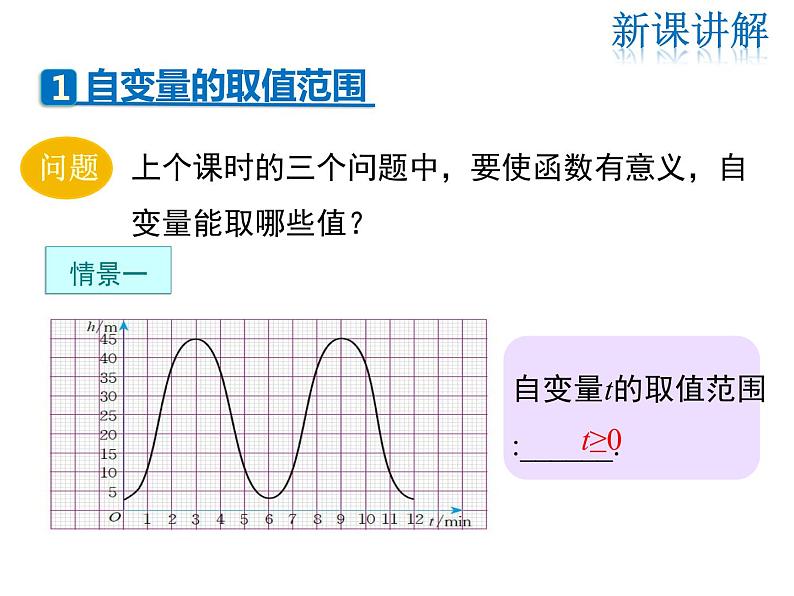
上个课时的三个问题中,要使函数有意义,自变量能取哪些值?
自变量t的取值范围:______.
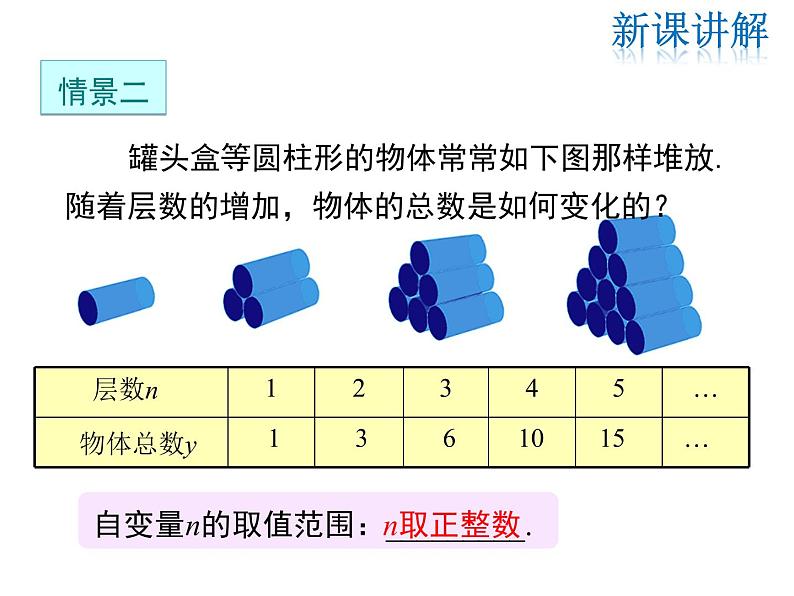
罐头盒等圆柱形的物体常常如下图那样堆放.随着层数的增加,物体的总数是如何变化的?
自变量n的取值范围:_________.
根据刚才问题的思考,你认为函数的自变量可以取任意值吗? 在实际问题中,函数的自变量取值范围往往是有限制的,在限制的范围内,函数才有实际意义;超出这个范围,函数没有实际意义,我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
解:根据等腰三角形的性质和三角 形内角和定理,得 2x+y=180°, 有y=180°-2x. 由于等腰三角形的底角只能是 锐角,所以自变量的取值范围是 0<x<90°.
等腰三角形顶角的度数y是底角度数x的函数,试写出这个函数关系式,并求出自变量x的取值范围.
一定质量的气体在体积不变时,假若温度降低 到-273 ℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
自变量t的取值范围:________.
下列函数中自变量x的取值范围是什么?
求函数自变量的取值范围时,需要考虑:
(4)表达式是复合式时,自变量的取值是使各式成 立的公共解.
(3)表达式是偶次根式时,自变量的取值必须使被 开方数为非负数.表达式是奇次根式时,自变量 取全体实数;
(1)表达式是整式时,自变量取全体实数;
(2)表达式是分式时,自变量的取值要使分母不为0;
右图反映了摩天轮上的一点的高度h (m)与旋转时间t(min) 之间的关系,那么怎么表示它们各自大小呢?
已知函数
(1)求当x=2,3,-3时,函数的值;(2)求当x取什么值时,函数的值为0.
解:(1)当x=2时,y= ; 当x=3时,y= ; 当x=-3时,y=7. (2)令 解得x= 即当x= 时,y=0.
把自变量x的值代入关系式中,即可求出函数的值.
等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10 cm,CA与MN在同一直线上,开始时点A与点M重合,让△ABC向右运动,最后点A与点N重合.(1)试写出重叠部分面积y cm2与MA长度x cm之间的 函数关系式;
y与x之间的函数关系式为
(2)当点A向右移动1 cm时,重叠部分的面积是多少?
故当点A向右移动1 cm时,重叠部分的面积是 cm2.
解 :点A向右移动1 cm,即x=1,此时
汽车的油箱中有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶里程x(单位:km)的增加而减少,平均耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子.
解:(1) 函数关系式为 y = 50-0.1x.
0.1x表示的意义是什么?
(2)指出自变量x的取值范围;
(2) 由x≥0及50-0.1x ≥0, 得0 ≤ x ≤ 500,∴自变量x的取值范围是 0 ≤ x ≤ 500.
注意:确定自变量的取值范围时,不仅要考虑使函数表达式有意义,而且还要注意各变量所代表的实际意义.
汽车行驶里程,油箱中的油量均不能为负数!
(3)汽车行驶200 km时,油箱中还有多少油?
(3)当 x = 200时,y=50-0.1×200=30.
故当汽车行驶200 km时,油箱中还有30 L油.
问题二:x 、y 之间存在怎样的数量关系?这种数量关系可以以什么形式给出?
一个三角形的周长为y cm,三边长分别为 7 cm、3 cm和 x cm.
(1) 求y关于x的函数关系式;
分析:问题一:题中包含了哪些变量?分别 表示什么?
根据题设,得 y=x+7+3.
一个三角形的周长为y cm,三边长分别为 7 cm、3 cm和 x cm.
(2) 求自变量x的取值范围.
分析:三角形的三边关系应满足:两边之和大于第 三边,两边之差小于第三边,即7-3
注意:对于实际问题中的函数,自变量的取值要符合实际意义.
1.下列说法中,不正确的是( ) A.函数不是数,而是一种关系 B.多边形的内角和是边数的函数 C.一天中时间是温度的函数 D.一天中温度是时间的函数
2.下列各表达式不是表示y是x的函数的是( )
A. B.C. D.
3.求下列函数中自变量x的取值范围:
4.我市白天乘坐出租车收费标准如下:乘坐里程不超 过3千米,一律收费8元;超过3千米时,超过3千米 的部分,每千米加收1.8元.设乘坐出租车的里程为x(千米)(x为整数),相对应的收费为y(元). (1)请分别写出当0<x≤3和x>3时y与x的关系式, 并直接写出当x=2和x=6时对应的y值;
解:当0<x≤3时,y=8; 当x>3时,y=8+1.8(x-3)=1.8x+2.6. 当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:当0<x≤3和x>3时,y都是x的函数.理由:因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
5.一长方形的周长为8 cm,设它的长为x cm,宽为y cm. (1)求y关于x的函数关系式; (2)写出自变量的取值范围.
解:(1)y关于x的函数关系式为
(2)自变量的取值范围为
自变量对应的因变量的值
数学八年级下册17.1 变量与函数优秀ppt课件: 这是一份数学八年级下册17.1 变量与函数优秀ppt课件,文件包含华东师大版中学数学八年级下171变量与函数第2课时自变量的取值与函数值教学课件pptx、第17章函数及其图象171变量与函数第2课时docx、171变量与函数第2课时同步练习docx等3份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
八年级下册17.1 变量与函数教学课件ppt: 这是一份八年级下册17.1 变量与函数教学课件ppt,文件包含华师版数学八年级下册第2课时确定函数关系式及自变量的取值范围教学课件ppt、华师版数学八年级下册第2课时变量与函数2教案doc等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
初中数学华师大版八年级下册17.1 变量与函数教学ppt课件: 这是一份初中数学华师大版八年级下册17.1 变量与函数教学ppt课件,文件包含华师版数学八年级下册第1课时变量与函数教学课件ppt、华师版数学八年级下册第1课时变量与函数1教案doc等2份课件配套教学资源,其中PPT共30页, 欢迎下载使用。













