华师大版八年级下册第19章 矩形、菱形与正方形19.1 矩形2. 矩形的判定教学课件ppt

这是一份华师大版八年级下册第19章 矩形、菱形与正方形19.1 矩形2. 矩形的判定教学课件ppt，共31页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，由直角的个数判定矩形，判定定理1，平行四边形的判定，对角线互相平分且相等等内容，欢迎下载使用。

由直角的个数判定矩形由对角线的关系判定矩形
我们已经知道，有一个角是直角的平行四边形是矩形，这是矩形的定义，我们可以依此判定一个四边形是否是矩形. 除此之外，我们能否找到其他判定矩形的方法呢?矩形是特殊的平行四边形，具有如下性质：1.四个角都是直角；2.两条对角线相等.这些性质，对我们寻找判定矩形的方法有什么启示?
矩形的判定：方法一(定义判定)：有一个角是直角的平行四边形是矩形；方法二(角判定)：有三个角是直角的四边形是矩形；
易错警示：用定义判定一个四边形是矩形必须满足两个条件：一是有一个角是直角，二是四边形是平行四边形．也就是说有一个角是直角的四边形不一定是矩形，必须加上“平行四边形”这个条件它才是矩形．
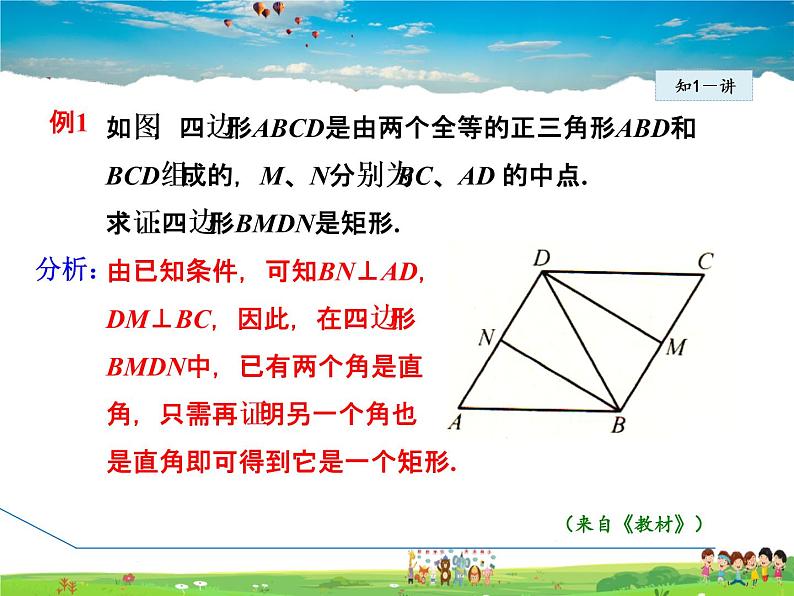
如图，四边形ABCD是由两个全等的正三角形ABD和BCD组成的，M、N分别为BC、AD 的中点.求证:四边形BMDN是矩形.
由已知条件，可知BN⊥AD，DM⊥BC，因此，在四边形BMDN中，已有两个角是直角，只需再证明另一个角也是直角即可得到它是一个矩形.
∵△ABD和△BCD是全等的正三角形，∴∠ADB＝∠CDB＝60°.又∵M、N分别为BC、AD的中点，∴BN⊥AD，DM⊥BC，∠BDM＝30°，∴∠DNB＝∠DMB＝90°，∠MDN＝∠ADB＋∠BDM＝90°,∴四边形BMDN是矩形(有三个角是直角的四边形是矩形).
如图， ABCD的四个内角的平分线分别相交于点E，F，G，H. 求证：四边形EFGH是矩形．
要证明四边形EFGH是矩形，由于已知ABCD的四个内角的平分线分别相交于点E，F，G，H，因此可选用“有三个角是直角的四边形是矩形”来证明．
∵AB∥CD，∴∠ABC＋∠BCD＝180°.∵BG平分∠ABC，CG平分∠BCD，∴∠GBC＋∠GCB＝ ×180°＝90°，∴∠BGC＝90°.同理可得∠AFB＝∠AED＝90°.∴∠GFE＝∠FEH＝∠FGH＝90°.∴四边形EFGH是矩形．
本题目中的图形是建立在平行四边形基础上，而条件中又涉及角的关系，一般采用“角的方法”来判定矩形．
1　如图，AB、CD是⊙O的两条直径，四边形ACBD是矩形吗？证明你的结论.
2　在 ABCD中，增加下列条件中的一个，就能判定它是矩形的是(　　)A．∠A＋∠C＝180° B．AB＝BCC．AC⊥BD D．AC＝2AB
3　数学课上，老师要同学们判断一个四边形门框是否为矩形．下面是某合作小组的4位同学给出的方案，其中正确的是(　　)A．测量对角线是否互相平分B．测量两组对边是否分别相等C．测量一组对角是否都为直角D．测量三个角是否都为直角
由对角线的关系判定矩形
矩形的判定：方法三(对角线判定)：对角线相等的平行四边形是矩形；或对角线相等且互相平分的四边形是矩形．要点精析：(1)矩形的判定与性质是互逆定理；(2)判定矩形的常见思路如图：
易错警示：用对角线相等的平行四边形是矩形判定一个四边形是矩形必须满足两个条件：一是对角线相等，二是四边形是平行四边形．也就是说两条对角线相等的四边形不一定是矩形，必须加上“平行四边形”这个条件它才是矩形．
如图，点O是矩形ABCD的对角线AC与BD的交点，E、F、G、H分别是AO、BO、CO、DO上的一点，且AE＝BF＝CG＝DH.求证：四边形EFGH是矩形.
根据已知条件，我们可以先证明四边形EFGH是平行四边形，再证明对角线EG和FH相等，即可得证.
∵四边形ABCD是矩形，∴AO＝BO＝CO＝DO.∵AE＝BF＝CG＝DH,∴OE＝OF＝OG＝OH，∴四边形EFGH是平行四边形.∵EO＋OG＝FO＋OH，即EG＝FH，∴四边形EFGH是矩形(对角线相等的平行四边形是矩形).
如图，在△ABC中，AB＝AC，AD⊥BC，垂足为点D，AG是△ABC的外角∠FAC的平分线，DE∥AB，交AG于点E. 求证：四边形ADCE是矩形.
根据已知条件AB＝AC ，我们可以先通过证明四边形ABDE是平行四边形，得到DE＝AB＝AC，因此可以利用“对角线相等的平行四边形是矩形”这一判定定理.
∵ AB＝AC，AD⊥BC， ∴∠B＝∠ACB，BD＝DC.又∵AE是△ABC的外角∠CAF的平分线，∴∠1＝ ∠CAF＝ (∠B＋∠ACB) ＝∠B，∴AE∥BC.又∵AB∥DE，∴四边形ABDE是平行四边形，∴AE＝BD，AB＝DE，∴AC＝DE，AE＝DC.又∵AE∥DC，∴四边形ADCE是平行四边形，∴四边形ADCE是矩形(对角线相等的平行四边形是矩形）. 
〈探究题〉如图，在矩形ABCD中，AB＝2，BC＝5，E、P分别在AD、BC上，且DE＝BP＝1，AP，BE相交于点H，CE，DP相交于点F.(1)判断△BEC的形状，并说明理由；(2)判断四边形EFPH是什么特殊四边形，并证明你的判断．
根据矩形性质得出CD＝2，AD＝5，根据勾股定理求出CE和BE，进而求出CE2＋BE2，BC2，根据勾股定理的逆定理即可判断△BEC的形状；
(1)判断△BEC的形状，并说明理由；
(1)△BEC是直角三角形．理由：∵四边形ABCD是矩形，∴∠ADC＝∠EAB＝90°，AD＝BC＝5，CD＝AB＝2，由勾股定理得：CE＝同理BE＝ ，∴CE2＋BE2＝5＋20＝25.∵BC2＝52＝25，∴BE2＋CE2＝BC2，∴∠BEC＝90°，∴△BEC是直角三角形．
根据矩形的性质和平行四边形的判定，推出四边形DEBP和四边形AECP均为平行四边形，进而推出四边形EFPH为平行四边形，根据矩形的判定即可得出结论．
(2)判断四边形EFPH是什么特殊四边形，并证明你的判断．
(2)四边形EFPH为矩形． ∵四边形ABCD是矩形，∴AD＝BC，AD∥BC. ∵DE＝BP，DE∥BP， ∴四边形DEBP是平行四边形，∴BE∥DP. ∵AD＝BC，AD∥BC，DE＝BP， ∴AE＝CP，AE∥CP， ∴四边形AECP是平行四边形， ∴AP∥CE，∴四边形EFPH是平行四边形． ∵∠BEC＝90°，∴平行四边形EFPH是矩形．
本题综合考查了勾股定理及其逆定理，矩形、平行四边形的性质和判定等知识，主要培养学生分析问题和解决问题的能力．
1　如图，将 ABCD的边DC延长到点E使CE＝DC，连结AE，交BC于点F，∠AFC＝2∠D，连结AC、BE.求证：四边形ABEC是矩形.
2　下列四边形：①对角线互相平分的四边形；②对角线相等的四边形；③对角线相等的平行四边形；④对角线互相平分且相等的四边形．其中一定是矩形的个数是(　　)A．1个 B．2个 C．3个 D．4个
3　在 ABCD中，对角线AC，BD相交于点O，再添加一个条件，仍不能判定四边形ABCD是矩形的是(　　)A．AB＝AD B．OA＝OBC．AC＝BD D．DC⊥BC
4　对于四边形ABCD，给出下列6组条件：①∠A＝90°，∠B＝∠C＝∠D；②∠A＝∠B＝90°，∠C＝∠D；③∠A＝∠B＝∠C＝∠D；④∠A＝∠B＝∠C＝90°；⑤AC＝BD；⑥AB∥CD，AD∥BC.其中能得到“四边形ABCD是矩形”的有(　　)A．1组 B．2组 C．3组 D．4组
有一个角是直角(定义)