【专项练习】备战中考数学58种模型专练 44.三角形“垂心”定理的7种证法（含答案）

这是一份【专项练习】备战中考数学58种模型专练 44.三角形“垂心”定理的7种证法（含答案），共4页。试卷主要包含了1定理，三角形“外心”定理， 三角形“内心”定理等内容，欢迎下载使用。
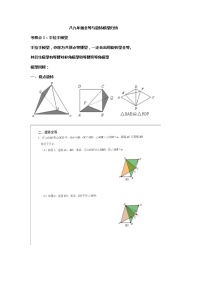
三角形“垂心”定理的7种证法  三角形“垂心”定理的证法 1.1定理：   三角形三条高相交于一点，这点叫做三角形的垂心（该定理俗称三角形“垂心”定理）.    已知，如图（1）中,AD,BE,CF分别是边BC,CA,AB上的高.      求证: AD,BE,CF相交于一点  1.2预备定理:    1.塞瓦(Ceva)定理:设D、E、F分别是三边BC、CA、AB上的点,若,则AD,BE,CF交于一点.2.三角形“外心”定理:三角形三边的中垂线相交于一点,此点与三顶点等距,这点叫做三角形的外心.3. 三角形“内心”定理:三角形三内角平分线交于一点,此点与三边等距,这点叫做三角形的内心. 1.3定理的证法   1.3.1证法1   如图（1），由已知可得，∽∽，∽三式相乘得：由塞瓦定理可得AD，BE，CF相交于一点. 1.3.2证法2如图（2）分别过A、B、C做它们所在高的垂线，使之相交成.则同理，可见，CF为边的中垂线。同理可得，BE为边的中垂线，AD为边的中垂线.为三边上的中垂线.由“外心”定理可知，AD、BE、CF相交于一点.        1.3.3证法3如图（3）连结DE，EF，FD，则A、B、D、E四点共圆，在和中，易知，又A、F、D、C四点共圆，，.可见，AD平分.同理可得，BE平分，CF平分.在中，由“内心”定理可得，AD，BE，CF相交于一点.   1.3.4证法4如图（4）设AB边上的高CF与BC边上的高AD相交于H，连结BH并延长交AC于E.连结DF，因A、F、D、C四点共圆，又B、D、H、F四点共圆，，在 和中中，可知，，BE为边AC上的高.由此可见，高AD、BE、CF相交于一点.         1.3.5证法5如图（5）设边BC，AC上的高AD，BE相交于H.连结DE，作于F。连结CH，   则A、B、D、E四点共圆，又与互余，与互余.又C、E、H、D四点共圆，，。又，，C、H、F三点共线。即AB边上的高CF经过H点。因而三条高AD、BE、CF相交于一点.  1.3.6证法6如图（6）设BC边上的高AD与AB边上的高CF相交于H，连结BH并延长交AC于E.建立如图所示的直角坐标系，并设A、B、C三点的坐标分别为：A（0，a），B（b,0），C（c,0）,则即BE为AC边上的高。可见高AD、BE、CF相交于一点. 1.3.7证法7如图（7），设边BC上的高AD与AB边上的高CF相交于H，连结BH并延长交AC于E。设，，则。即， 即可见，， 即BE是AC边上的高.三边上的高AD、BE、CF相交于一点.   上述7种证法中，其中证法2是由高斯最早发现的，所以此证法又叫做高斯“外心”证法。证法3是由杨乐（我国数学家）最早（读初中时）发现的，所以此证法又叫做杨乐“内心”证法。其余证法是由后人所创.