【专项练习】备战中考数学58种模型专练 52.阿基米德折弦定理的四种常规证法（含答案）

阿基米德折弦定理的四种常见证法

                                            Justin ● 深圳

平面几何内容在整个初中数学知识中占有很重要第位，无论是中考还是平时阶段检测，往往会在几何题目的设置上体现选拔性。更有人说：“初中数学学得好不好，关键看几何好不好”。这些虽然仅仅是一些说法而已，但也不无它的道理。平面几何的确是考察学生的一个很重要的方面，几何学习的关键主要是掌握作辅助线的技巧。而这些技巧也并非一朝一夕就能掌握的，需要长时间的积累，总结，并应用才能较好掌握。在整个初中范围内，圆作为一个独立的章节更显现它的重要，并以综合难度大，辅助线的作法较多著称。下面就以“阿基米德折弦定理”的证明为例来浅谈本人对圆的学习心得。

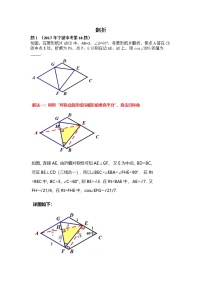
问题：已知M 为弧AC的中点，B为弧AM上任意一点，且MD⊥BC于D.求证：AB+BD=DC

证法一：(补短法)

如图：延长DB至F，使BF=BA     ∵M 为     的中点     ∴AM=MC,

 ∴∠MAC=∠MCA---①    又∵,  ∴MC=MA    ∴∠MBC=∠MAC---②

又∵∠MBC+∠MBF=180---③    由M,B,A,C四点共圆    ∴∠MCA+∠MBA=180---④

由①②③④可得：∠MBA=∠MBF

在△MBF与△MBA中：

∴△MBF△MBA(SAS)   ∴MF=MA, 又∵MC=MA  ∴MF=MC

又∵MD⊥CF  ∴DF=DC  ∴FB+BD=DC  又∵BF=BA  

∴AB+BD=DC（证毕）

证法二：（截长法）

如图：在CD上截取DB=DG   ∵MD⊥BG  ∴MB=MG  ∴∠MBG=∠MGB---①

又∵，∴∠MBG=∠MAC   又∵∠MAC=∠MCA  (已证)，

∴∠MBG=∠MCA---②   由①②可得∠MGB=∠MCA=∠BCA+∠MCG

而∠MGB=∠GMC+∠MCG  ∴∠GMC=∠BCA   又∵,∴∠BMA=∠BCA 

∴∠BMA=∠GMC,  在△MBA与△MGC中 ∴△BMA△GMC (SAS)

∴AB=GC, ∴AB+BD=GC+BD=GC+DG=DC(证毕)

证法三：（翻折）

如图：连接MB,MC,MA,AC, 将△BAM沿BM翻折，使点A落至点E，连接ME,BE

∵△MBA与△MBE关于BM对称，所以△MBE≌MBA  ∴MA=ME,  ∠MBA=∠MBE-①

又∵MA=MC, ∴ME=MC ,   又∵M, B, A, C四点共圆，

∴∠MBA+∠MCA=180---②  又∵MA=MC(已证) ∴∠MAC=∠MCA

又∵，∴∠MBC=∠MAC  ∴∠MBC=∠MCA- --③

由①②③得:∠MBC+∠MBE=180  ∴E,B,C三点共线。 又∵ME=MC,MD⊥CE

∴DE=DC ,∴EB+BD=DC ,又∵△MBE≌MBA ∴AB=EB

∴ AB+BD=DC(证毕)

证法四：如图，连接MB,MA,MC,AC, 延长AB,过点M作MH⊥AB于点H,

∵M 为的中点     ∴AM=MC,   又∵,∴∠HAM=∠DCM

又∵∠MHA=∠MDC=90  ∴在△MHA与△MDC中 

∴△MHA≌△MDC (AAS)   ∴CD=AH---①    MD=MH  在RT△MHB与RT△MDB中

∴△MDB≌△MHB (HL) ∴BD=BH  又∵AH=AB+BH,  ∴AH=AB+BD-②

由①②可得DC=AB+BD  (证毕)

反思：在平时数学教学活动中，尤其是几何学的教学，它可以让觉得数学课枯燥无味的学生顿时感兴趣，更是师生互动的一个很好的媒体。老师与学生一起想办法，也是一种数学情感的体现。在圆这一章节，很多学生反映难学，难在辅助线多，方法多，同一个问题灵活多变，不同的出发点会得到不同的解题方法。本题就是一个很好的例子。对于一个著名的平面几何定理，我们的证明也仅仅是使用了非常常见的“截长补短”，“对称变换”等方法。在以后的几何教学过程中多总结出一些通用，常见的解题方法这会让学生受益匪浅的，万变不离其宗，才是数学的特点。