【专项练习】备战中考数学58种模型专练 4.角平分线模型，截取构造对称全等（含答案）

这是一份【专项练习】备战中考数学58种模型专练 4.角平分线模型，截取构造对称全等（含答案），共6页。
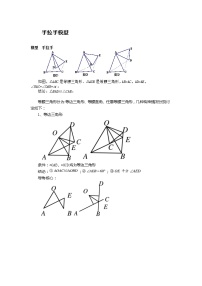
角平分线模型 模型 2 截取构造对称全等 如图，P 是∠MON 的角平分线上一点，点 A 是射线 OM 上任意一点，在 ON 上截取 OB=OA，连接 PB。 结论：△OPB≌△OPA。  模型证明：∵OP 是∠MON 的角平分线∴∠AOP=∠BOP，OP=OP又OA=AB∴△OPB≌△OPA       模型分析利用角平分线图形的对称性，在角的两边构造对称全等三角形，可以得 到对应边、对应角相等。利用对称性把一些线段或角进行转移，这是经常使 用的一种解题技巧。              模型实例 （1）如图①所示，在△ABC 中，AD 是△ABC 的外角平分线，P 是 AD 上异于点 A 的任意一点，试比较 PB+PC 与 AB+AC 的大小，并说明理由； （2）如图②所示， AD 是△ABC 的内角平分线，其他条件不变，试比较 PC-PB 与 AC-AB 的大小，并说明理由。         解:（1）如图在BA的延长线上取点E使AE=AC，连接PC由角平分线模型2可证△APC≌△APE∴PC=PE∴在△PBE中有PC+PE>BE=AB+AE∴PB+PC>AB+AC
     （2）如图在AC上取一点E使AE=AB，连接PE     ∵∠BAP=∠EAP,AP=AP,AE=AB     ∴△BAP≌△EAP     ∴PB=PE在△PEC中，PC-PB=PC-PE>EC=AC-AE=AC-AB∴PC-PB>AC-AB
        模型练习1．已知，在△ABC 中，∠A=2∠B，CD 是∠ACB 的平分线，AC=16，AD=8。 求线段 BC 的长。            解：如图在CB上取一点E使CE=CA，则有CD=CD，∠ACD=∠ECD∴△ACD≌ECD∴AD=DE=8∴∠A=∠CED=2∠B又∠CED=∠B+∠BDE∴∠B=∠BDE∴△BDE为等腰三角形∴DE=BE=8又CE=CA=16∴BC=BE+EC=24       2．已知，在△ABC 中，AB=AC，∠A=108°，BD 平分∠ABC。 求证：BC=AB+CD。              解：如图在BC上取一点E使BA=BE,则BD=BD,∠ABD=∠EBD∴△ABD≌△EBD∴AB=EB，∠DEB=108°又∠C=36°∴∠CDE=∠CED=72°∴CD=CE∴BC=AB+CD 
      3．如图所示，在△ABC 中，∠A=100°，∠ABC=40°，BD 是∠ABC 的平分线，延 长 BD 至 E，DE=AD。求证：BC=AB+CE。