高中数学北师大版 (2019)必修 第一册4.1 样本的数字特征随堂练习题

这是一份高中数学北师大版 (2019)必修 第一册4.1 样本的数字特征随堂练习题，共19页。试卷主要包含了1　样本的数字特征，下列说法中,不正确的是，5和17B，5D等内容，欢迎下载使用。

基础过关练
题组一 平均数、中位数、众数
1.下列说法中,不正确的是( )
A.数据2,4,6,8的中位数是4,6
B.数据1,2,2,3,4,4的众数是2,4
C.一组数据的平均数、中位数、众数有可能是同一个数据
D.8个数据的平均数为5,另3个数据的平均数为7,则这11个数据的平均数是8×5+7×311
2.(2019北京四中高一期中)10名工人生产某一零件,生产的件数分别是10,12,14,14,15,15,16,17,17,17.设其平均数为a,中位数为b,众数为c,则( )
A.a>b>cB.b>c>a
C.c>a>bD.c>b>a
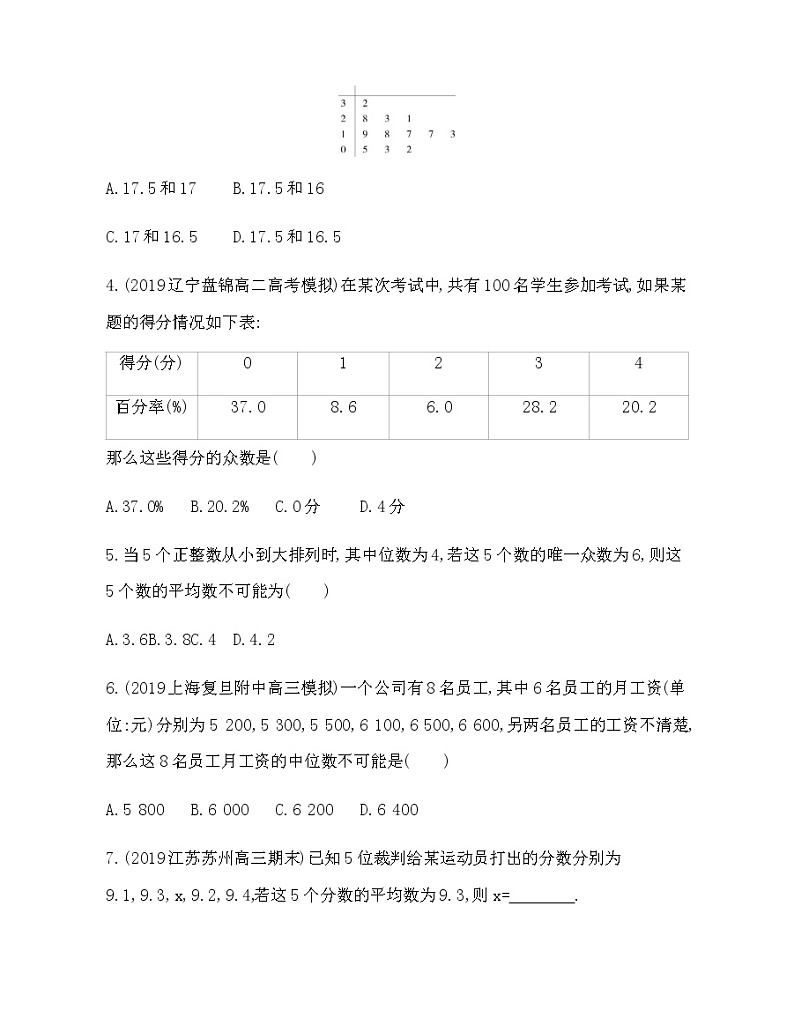
3.(2020四川成都棠湖中学高三期末)2019年第十三届女排世界杯共12支队伍参加,中国女排不负众望荣膺十冠王.将12支队伍的积分制成茎叶图如图所示,则这组数据的中位数和平均数分别为( )
A.17.5和17B.17.5和16
C.17和16.5D.17.5和16.5
4.(2019辽宁盘锦高二高考模拟)在某次考试中,共有100名学生参加考试,如果某题的得分情况如下表:
那么这些得分的众数是( )
A.37.0%B.20.2%C.0分D.4分
5.当5个正整数从小到大排列时,其中位数为4,若这5个数的唯一众数为6,则这5个数的平均数不可能为( )
A.3.6B.3.8C.4D.4.2
6.(2019上海复旦附中高三模拟)一个公司有8名员工,其中6名员工的月工资(单位:元)分别为5 200,5 300,5 500,6 100,6 500,6 600,另两名员工的工资不清楚,那么这8名员工月工资的中位数不可能是( )
A.5 800B.6 000C.6 200D.6 400
7.(2019江苏苏州高三期末)已知5位裁判给某运动员打出的分数分别为9.1,9.3,x,9.2,9.4,若这5个分数的平均数为9.3,则x= .
题组二 极差、方差、标准差
8.样本101,98,102,100,99的标准差为( )
A.2B.0C.1D.2
9.为了稳定市场,确保农民增收,某农产品3月份以后的每月市场收购价格(单位:元/担)与其前3个月的市场收购价格有关,并与前3个月的月市场收购价格之差的平方和最小,下表列出的是该产品今年前6个月的月市场收购价格,则前7个月该产品的月市场收购价格的方差为( )
A.757B.767C.11D.787
10.(2020辽宁沈阳高三期末)若一组数据的平均数为m,方差为n,将这组数据的每个数都乘a(a>0)得到一组新数据,则下列说法正确的是( )
A.这组新数据的平均数为m
B.这组新数据的平均数为a+m
C.这组新数据的方差为an
D.这组新数据的标准差为an
11.(2019河南洛阳第一高级中学高一月考)某班有48名学生,在一次考试中统计出平均分数为70,方差为75,后来发现有2名同学的成绩有误,甲实得80分却记为50分,乙实得70分却记为100分,更正后平均分和方差分别是( )
A.70,25B.70,50C.70,52D.65,25
12.(2020四川眉山一中高一模拟)若40个数据的平方和是56,平均数是22,则这组数据的方差是 ,标准差是 .
13.一组样本数据按从小到大的顺序排列为-1,0,4,x,y,14,若这组数据的平均数与中位数均为5,则其方差为 .
14.(2019陕西西安长安一中高二期末)一组数据的平均数是28,方差是4,若将这组数据中的每一个数据都加上20,得到一组新数据,求所得新数据的平均数和方差.
题组三 数据的数字特征及应用
15.已知数据x1,x2,x3,…,xn是某市普通职工n(n≥3,n∈N*)个人的年收入,设这n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入xn+1,那么关于这(n+1)个数据的说法正确的是( )
A.平均数大大增大,中位数一定变大,方差可能不变
B.平均数大大增大,中位数可能不变,方差变大
C.平均数大大增大,中位数可能不变,方差也不变
D.平均数可能不变,中位数可能不变,方差可能不变
16.(2019广西桂林高一月考)如图所示,样本A和B分别取自两个不同的总体,它们的样本平均数分别为xA和xB,样本标准差分别为sA和sB,则( )
A.xA>xB,sA>sBB.xAsB
C.xA>xB,sA17.在某次测量中得到的A样本数据如下:52,54,54,56,56,56,55,55,55,55.若B样本数据恰好是A样本数据都加6后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A.众数B.平均数
C.中位数D.标准差
18.(2019河南郑州高三期末)某市体育局将从甲、乙、丙、丁四人中选一人参加全省100米仰泳比赛,现将他们最近集训的10次成绩(单位:秒)的平均数与方差制成表格如下:
根据表中的数据,应选 选手参加比赛( )
A.甲B.乙
C.丙D.丁
19.(2020浙江绍兴一中模拟)甲、乙两名同学在高考前各做5次立定跳远测试,测得甲的成绩(单位:米)如下:2.20,2.30,2.30,2.40,2.30.若甲、乙两人的平均成绩相同,乙的成绩的方差是0.005,则甲、乙两人成绩较稳定的是 .
20.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82,81,79,78,95,88,93,84;
乙:92,95,80,75,83,80,90,85.
(1)指出乙学生成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均数和方差的角度考虑,你认为派哪位学生参加合适?请说明理由.
题组四 用样本的数字特征估计总体的数字特征
21.(2019湖北襄阳四中模拟)某班有50名学生,男、女生人数不相等.随机询问了该班5名男生和5名女生的某次数学测试成绩,用茎叶图记录如图所示,则下列说法正确的是( )
A.这5名男生成绩的标准差大于这5名女生成绩的标准差
B.这5名男生成绩的中位数大于这5名女生成绩的中位数
C.该班男生成绩的平均数大于该班女生成绩的平均数
D.这种抽样方法是分层随机抽样
22.为比较甲、乙两地某月14时的气温状况,随机选取该月中的5天,将这5天中14时的气温数据(单位:℃)制成如图所示的茎叶图.根据图中数据可估计:
①甲地该月14时的平均气温低于乙地该月14时的平均气温;
②甲地该月14时的平均气温高于乙地该月14时的平均气温;
③甲地该月14时的气温的标准差小于乙地该月14时的气温的标准差;
④甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
其中根据茎叶图能得到的统计结论的序号为 .
能力提升练
题组一 数据的数字特征及性质应用
1.(2019江西南昌高三高考模拟,)某村前三年的经济收入(单位:万元)分别为100,200,300,其统计数据的中位数为x,平均数为y.经过今年政府新农村建设后,该村经济收入在上年基础上翻番,则在这四年收入的统计数据中,下列说法正确的是( )
A.中位数为x,平均数为1.5y
B.中位数为1.25x,平均数为y
C.中位数为1.25x,平均数为1.5y
D.中位数为1.5x,平均数为2y
2.(2020云南大理高一月考,)已知一组数据x1, x2, x3, x4, x5的平均数是3,方差是12,则另一组数据2x1-1,2x2-1,2x3-1,2x4-1,2x5-1的平均数,方差分别是(深度解析)
A.5,12B.5,2
C.3,2D.3,12
3.(多选)(2020福建龙岩上杭一中高一月考,)乐乐家共有七人,已知今年这七人年龄的众数为35,平均数为44,中位数为55,标准差为19,则5年后,下列说法正确的是( )
A.这七人年龄的众数变为40
B.这七人年龄的平均数变为49
C.这七人年龄的中位数变为60
D.这七人年龄的标准差变为24
4.(2020广西桂林高二月考,)某人5次上班途中所花的时间(单位:分钟)分别为x,y,10,11,9.若这组数据的平均数为10,方差为2,则|x-y|的值为 .
题组二 统计图表与数字特征的综合应用
5.(多选)(2019广东深圳高考模拟,)在某次高中学科知识竞赛中,对4 000名考生的参赛成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],60分以下视为不及格,若同一组中数据用该组区间中点值作代表,则下列说法正确的是( )
A.成绩在[70,80)的考生人数最多
B.不及格的考生人数为1 000
C.考生竞赛成绩的平均分约为70.5分
D.考生竞赛成绩的中位数为75分
题组三 样本数字特征中的决策性问题
6.(2020河北唐山一中高三月考,)气象意义上从春季进入夏季的标志为“连续5天的日平均温度均不低于22 ℃”.现有甲、乙、丙三地连续5天的日平均温度(单位:℃)的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体平均数为24;
③丙地:5个数据中有一个数据是32,总体平均数为26,总体方差为10.8.
则肯定进入夏季的地区有( )
A.0个B.1个C.2个D.3个
7.(2019吉林辽源高一月考,)两台机床同时生产直径为10 mm的零件,为了检验产品质量,质量检验员从两台机床生产的产品中各抽出4件进行测量(单位:mm),结果如下:
若你是质量检验员,在收集到上述数据后,你将通过怎样的运算来判断哪台机床生产的零件质量更符合要求?
答案全解全析
基础过关练
1.A 数据2,4,6,8的中位数为4+62=5,显然选项A中说法是不正确的,选项B,C,D中说法都是正确的.故选A.
2.D 依题意,得
a=10+12+14+14+15+15+16+17+17+1710=14.7,中位数b=15,众数c=17,故c>b>a,故选D.
3.D 由茎叶图可得这12个数据分别为2,3,5,13,17,17,18,19,21,23,28,32.根据中位数的概念可得这组数据的中位数为17.5,
根据平均数的概念可得这组数据的平均数为2+3+5+13+17+17+18+19+21+23+28+3212=16.5.故选D.
4.C 由题意得,得分为0分的百分率为37.0%,所占比例最大,所以这些得分的众数是0分,故选C.
5.A 设这5个数从小到大排列为a1,a2,a3,a4,a5,依题意得a3=4,a4=a5=6,a1,a2是1,2,3中两个不同的数,符合题意的5个数的可能情况有三种:“1,2,4,6,6”“1,3,4,6,6”“2,3,4,6,6”,其平均数分别为3.8,4,4.2,因此平均数不可能为3.6.故选A.
6.D ∵该公司有8名员工,其中6名员工的月工资(单位:元)分别为5 200,5 300,5 500,6 100,6 500,6 600,
∴当另外两名员工的月工资都小于5 200元时,中位数为(5 300+5 500)÷2=5 400;
当另外两名员工的月工资都大于6 600元时,中位数为(6 100+6 500)÷2=6 300,
∴这8名员工月工资的中位数的取值区间为[5 400,6 300],
∴这8名员工月工资的中位数不可能是6 400.故选D.
7.答案 9.5
解析 数据9.1,9.3,x,9.2,9.4的平均数为
15×(9.1+9.3+x+9.2+9.4)=9.3,解得x=9.5.
8.A 由题意可得样本平均数x=100,方差s2=2,故标准差s=2,故选A.
9.B 设7月份的月市场收购价格为x元,则其与前3个月的月市场收购价格之差的平方和为(x-71)2+(x-72)2+(x-70)2,经检验,当x=71时,平方和最小,此时可求得方差为767.
10.D 根据题意知,这组新数据的平均数为am,方差为a2n,标准差为an.故选D.
11.B 甲少记30分,乙多记30分,则总分不变,由此知平均分不发生变化.
设其余46名学生的成绩分别为x1,x2,…,x46,则原方差s2=148[(x1-70)2+(x2-70)2+…+(x46-70)2+(50-70)2+(100-70)2]=75,更正后方差s'2=148[(x1-70)2+(x2-70)2+…+(x46-70)2+(80-70)2+(70-70)2]=s2-148[(50-70)2+(100-70)2]+148[(80-70)2+(70-70)2]=50,
故选B.
12.答案 0.9;31010
解析 设这40个数据为xi(i=1,2,…,40),平均数为x,
则方差s2=140×[(x1-x)2+(x2-x)2+…+(x40-x)2]
=140[x12+x22+…+x402+40x2-2x(x1+x2+…+x40)]
=140×56+40×222-2×22×40×22
=140×36=0.9,
故标准差s=0.9=31010.
13.答案 743
解析 ∵数据-1,0,4,x,y,14的中位数为5,∴4+x2=5,∴x=6,∴这组数据的平均数是-1+0+4+6+y+146=5,∴y=7,∴这组数据的方差是16×(36+25+1+1+4+81)=743,故答案为743.
14.解析 设该组数据为x1,x2,…,xn,则新数据为x1+20,x2+20,…,xn+20.
∵原数据的平均数x=x1+x2+…+xnn=28,
∴新数据的平均数x'=x1+20+x2+20+…+xn+20n=20+28=48.
∵原数据的方差s2=1n[(x1-x)2+(x2-x)2+…+(xn-x)2],
∴新数据的方差s'2=1n{[x1+20-(x+20)]2+[x2+20-(x+20)]2+…+[xn+20-(x+20)]2},
∴s'2=s2=4.
15.B 插入大的极端值,平均数增加,中位数可能不变,方差也因为数据更加分散而变大.
16.B 由题图易得xA又A的波动性大,B的波动性小,
所以sA>sB.
17.D 由题意可知B样本的数据为58,60,60,62,62,62,61,61,61,61.
将A样本中的数据由小到大依次排列为52,54,54,55,55,55,55,56,56,56,
将B样本中的数据由小到大依次排列为58,60,60,61,61,61,61,62,62,62,
因此A样本数据的众数为55,B样本数据的众数为61,A选项错误;
A样本数据的平均数为54.8,B样本数据的平均数为60.8,B选项错误;
A样本数据的中位数为55,B样本数据的中位数为61,C选项错误;
事实上,在A样本的每个数据上加上6后形成B样本,样本的稳定性不变,因此两个样本的标准差相等,故选D.
18.D 100米仰泳比赛的成绩是时间越短越好,方差越小发挥水平越稳定,故丁是最佳人选.故选D.
19.答案 甲
解析 易得甲的平均成绩为2.30,甲的成绩的方差是0.004.由已知得甲、乙两人的平均成绩相同,但甲的成绩的方差比乙的小,所以甲的成绩较稳定.
20.解析 (1)将乙学生的成绩按从低到高的顺序排列:75,80,80,83,85,90,92,95.中间两个数是83,85,故乙学生成绩的中位数为84.
(2)派甲参加比较合适.理由如下:
x甲=18×(82+81+79+78+95+88+93+84)=85,
x乙=18×(92+95+80+75+83+80+90+85)=85,
s甲2=18×[(82-85)2+(81-85)2+(79-85)2+(78-85)2+(95-85)2+(88-85)2+(93-85)2+(84-85)2]=35.5,
s乙2=18×[(92-85)2+(95-85)2+(80-85)2+(75-85)2+(83-85)2+(80-85)2+(90-85)2+(85-85)2]=41,
∵x甲=x乙,s甲2∴甲的成绩比较稳定,派甲参加比较合适.
21.A 5名男生成绩的平均数为
90+92+94+86+885=90,
5名女生成绩的平均数为93+93+93+88+885=91,
这5名男生成绩的方差为15×[22+42+(-4)2+(-2)2]=8,女生成绩的方差为15×[22×3+(-3)2×2]=6,男生成绩的方差大于女生成绩的方差,所以男生成绩的标准差大于女生成绩的标准差,所以A正确;
这5名男生成绩的中位数是90,5名女生成绩的中位数是93,所以B错误;
该班男生和女生成绩的平均数可通过样本估计,但不能通过样本计算得到平均数的准确值,所以C错误;
男生和女生的人数不等,若采用分层随机抽样的方法,则抽取的人数也不相等,所以D错误.故选A.
22.答案 ①④
解析 由题中茎叶图中的数据,可得甲、乙两地该月14时的气温抽取的样本温度(单位:℃)分别为:
甲:26,28,29,31,31;
乙:28,29,30,31,32.
因此甲地该月14时的平均气温为15×(26+28+29+31+31)=29(℃),
乙地该月14时的平均气温为15×(28+29+30+31+32)=30(℃),
故甲地该月14时的平均气温低于乙地该月14时的平均气温.
由方差公式可得甲地该月14时的气温的方差为3.6,乙地该月14时的气温的方差为2,所以甲地该月14时的气温的标准差大于乙地该月14时的气温的标准差.
故选①④.
能力提升练
1.C 依题意,前三年收入数据的中位数x=200,平均数y=100+200+3003=200,第四年收入为600万元,故中位数为200+3002=250=1.25x,平均数为100+200+300+6004=300=1.5y,故选C.
2.B 因为数据x1, x2, x3, x4, x5的平均数x=3,方差为15×[(x1-3)2+(x2-3)2+(x3-3)2+(x4-3)2+(x5-3)2]=12,
所以数据2x1-1, 2x2-1,2x3-1,2x4-1,2x5-1的平均数为15×[(2x1-1)+(2x2-1)+(2x3-1)+(2x4-1)+(2x5-1)]=15×[2(x1+x2+x3+x4+x5)]-1=2×3-1=5,方差为15×[(2x1-1-5)2+(2x2-1-5)2+(2x3-1-5)2+(2x4-1-5)2+(2x5-1-5)2]=15×4×[(x1-3)2+(x2-3)2+(x3-3)2+(x4-3)2+(x5-3)2]=4×12=2.
故选B.
方法技巧 一般地,若x1, x2, x3,…, xn的平均数、方差分别为x、s2,则ax1+b, ax2+b, ax3+b,…, axn+b的平均数、方差分别为ax+b、a2s2.
3.ABC 根据众数、平均数、中位数的概念得5年后,每人的年龄相应增加5,而标准差不变,
所以这七人年龄的众数变为40;平均数变为49;中位数变为60;标准差不变,为19.
故选ABC.
4.答案 4
解析 由题意,得x+y=10×5-10-11-9=20,(x-10)2+(y-10)2=2×5-02-12-(-1)2=8,
设x=10+t,y=10-t,则2t2=8,解得t=±2,
∴|x-y|=2|t|=4.
5.ABC 由频率分布直方图可得,成绩在[70,80)的频率最高,因此成绩在[70,80)的考生人数最多,故A正确;
成绩在[40,60)的频率为0.010×10+0.015×10=0.25,因此,不及格的人数为
4 000×0.25=1 000,故B正确;
考生竞赛成绩的平均分约为45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5(分),故C正确;
因为成绩在[40,70)的频率为0.45,在[70,80)的频率为0.3,所以中位数为70+10×0.050.3≈71.67,故D错误.
故选ABC.
6.C 甲地:5个数据的中位数为24,众数为22,则甲地连续5天的日平均温度最低为22,所以其连续5天的日平均温度不低于22 ℃,所以甲地肯定进入夏季.
乙地:5个数据的中位数为27,总体平均数为24,当5个数据为19,20,27,27,27时,其连续5天的日平均温度有低于22 ℃的,不符合进入夏季的标准.
丙地:5个数据中有一个数据是32,总体平均数为26,若有低于22的,不妨取21,则方差超过了10.8,可以知道其连续5天的日平均温度不低于22 ℃,所以丙地肯定进入夏季.
综上所述,肯定进入夏季的地区有2个,故选C.
7.解析 ①x甲=14×(10+9.8+10+10.2)=10,
x乙=14×(10.1+10+9.9+10)=10,
由于x甲=x乙,因此,平均直径反映不出两台机床生产的零件的质量优劣.
②s甲2=14×[(10-10)2+(9.8-10)2+(10-10)2+(10.2-10)2]=0.02,
s乙2=14×[(10.1-10)2+(10-10)2+(9.9-10)2+(10-10)2]=0.005.
这说明乙机床生产出的零件直径波动小,因此,从产品质量稳定性的角度考虑,乙机床生产的零件质量更符合要求.
得分(分)
0
1
2
3
4
百分率(%)
37.0
8.6
6.0
28.2
20.2
月份
1
2
3
4
5
6
价格(元/担)
68
78
67
71
72
70
甲
乙
丙
丁
平均数
59
57
59
57
方差
12
12
10
10
机床甲
10
9.8
10
10.2
机床乙
10.1
10
9.9
10