语文版（中职）基础模块下册第八单元 直线与圆的方程8.8 直线与圆的方程的简单应用背景图课件ppt

这是一份语文版（中职）基础模块下册第八单元 直线与圆的方程8.8 直线与圆的方程的简单应用背景图课件ppt，共12页。PPT课件主要包含了创设情境兴趣导入，实际问题，建立函数模型，实际结果，数学结果，分析抽象转化，数学方法等内容，欢迎下载使用。

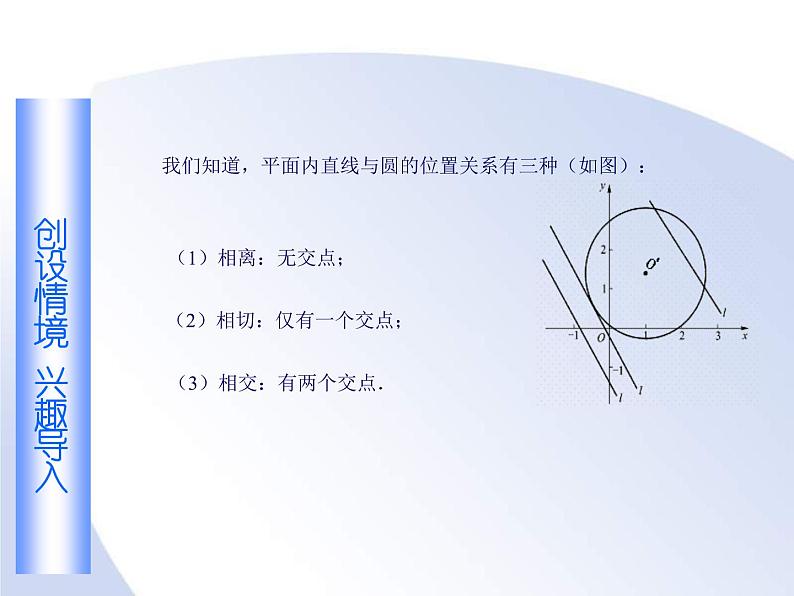
我们知道，平面内直线与圆的位置关系有三种（如图）：
（2）相切：仅有一个交点；
（3）相交：有两个交点．
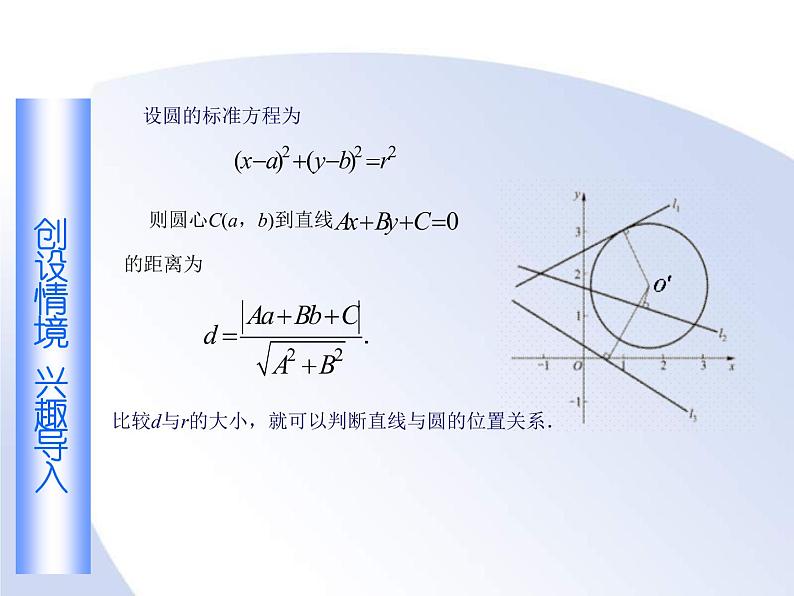
直线与圆的位置关系，可以由圆心到直线的距离d与半径r的关系
比较d与r的大小，就可以判断直线与圆的位置关系．
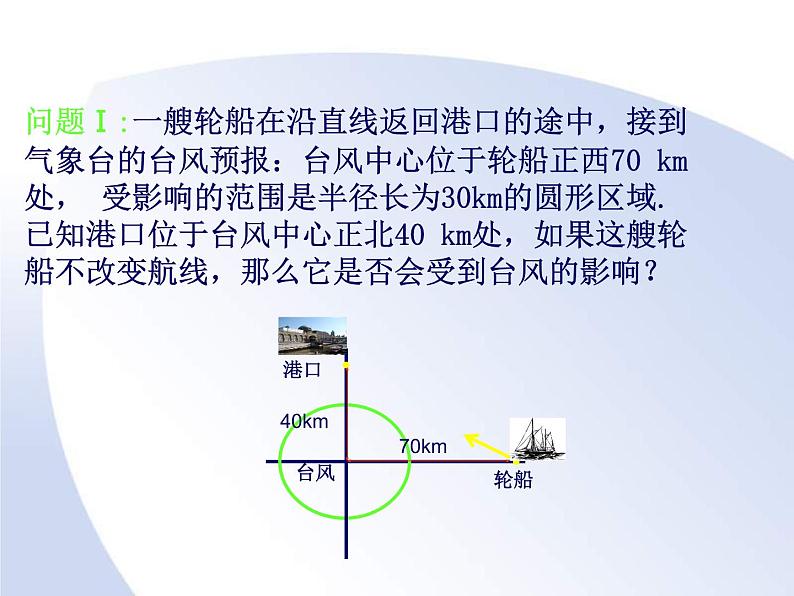
问题Ⅰ:一艘轮船在沿直线返回港口的途中，接到气象台的台风预报：台风中心位于轮船正西70 km处， 受影响的范围是半径长为30km的圆形区域. 已知港口位于台风中心正北40 km处，如果这艘轮船不改变航线，那么它是否会受到台风的影响？
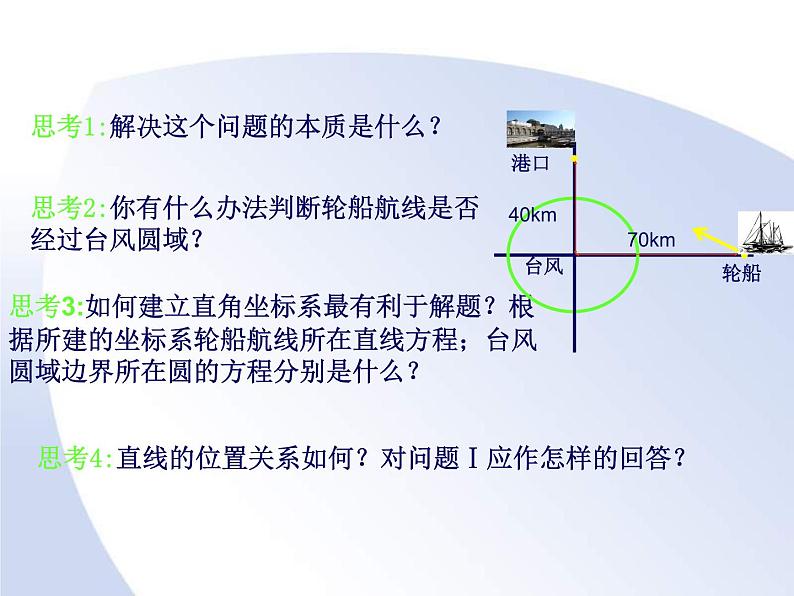
思考1:解决这个问题的本质是什么？
思考2:你有什么办法判断轮船航线是否经过台风圆域？
思考3:如何建立直角坐标系最有利于解题？根据所建的坐标系轮船航线所在直线方程；台风圆域边界所在圆的方程分别是什么？
思考4:直线的位置关系如何？对问题Ⅰ应作怎样的回答？
如图所示以台风中心为原点，轮船所在的方向为X轴的正方向，取10km为长度单位，建立直角坐标系。则
台风所在圆的方程为： x2＋y2＝9
轮船所在的直线AB方程为： 4x＋7y－28＝0
圆心（0，0）到直线4x＋7y－28＝0的距离为
r=3 d>r
所以这艘轮船不改变航线，不会受到台风的影响。
第二步：通过代数运算，解决代数问题；
用坐标法解决几何问题的步骤：
第一步：建立适当的平面直角坐标系，用坐标和方程表示问题中的几何元素，将平面几何问题转化为代数问题；
第三步：将代数运算结果“翻译”成几何结论．
方法总结：解决实际问题的数学思想方法
问题Ⅱ:某施工单位砌圆拱时，需要制作如图所示的木模．设圆拱高为1m，跨度为6 m，中间需要等距离的安装5根支撑柱子，求E点的柱子长度（精确到0.1m）．
思考1: 你能用几何法求支柱EP的高度吗？
思考2: 如图所示建立直角坐标系，那么求支柱EP的高度，化归为求一个什么问题？
思考3: 取1m为长度单位，如何求圆拱所在圆的方程？
思考4: 利用这个圆的方程可求得点P的纵坐标是多少？问题Ⅱ的答案如何？
解： 以点D为坐标原点，过AG的直线为x轴，建立直角坐标系，则点E的坐标为（1，0）, 圆心O’ 在y轴．
答　E点的柱子长度约为0.9 m．
设半径为r，则| O’O|2+| OG|2=| O’G|2