高中数学语文版（中职）基础模块下册9.2 直线、平面平行的判定与性质教案配套课件ppt

这是一份高中数学语文版（中职）基础模块下册9.2 直线、平面平行的判定与性质教案配套课件ppt，共26页。PPT课件主要包含了直线在平面内，直线与平面相交，直线与平面平行，知识回顾，文字语言，图形语言，符号语言，引入新课，观察1，实例感受等内容，欢迎下载使用。

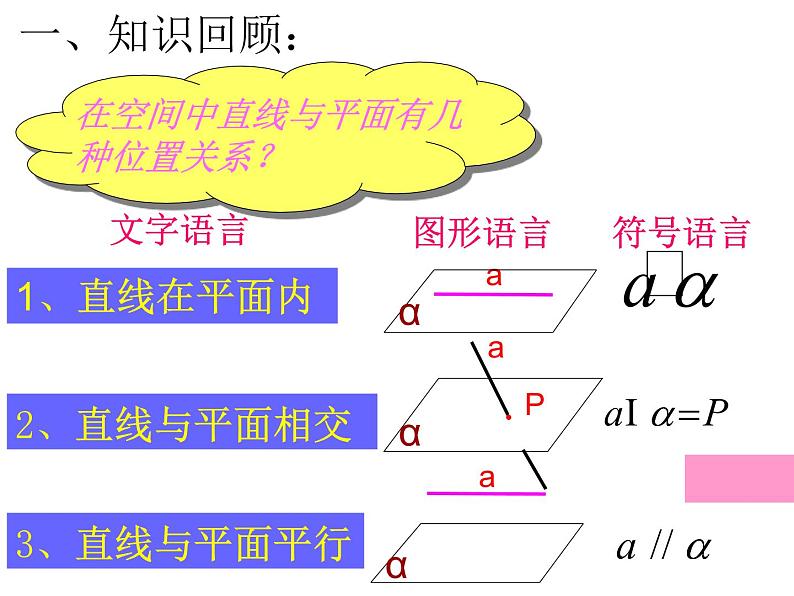
在空间中直线与平面有几种位置关系？
找出下图中的线面平行关系
根据定义，判定直线与平面是否平行，只需判定直线与平面没有公共点．
怎样判定直线与平面平行呢？
但是,直线无限伸长,平面无限延展.无法保证直线与平面没有公共点.
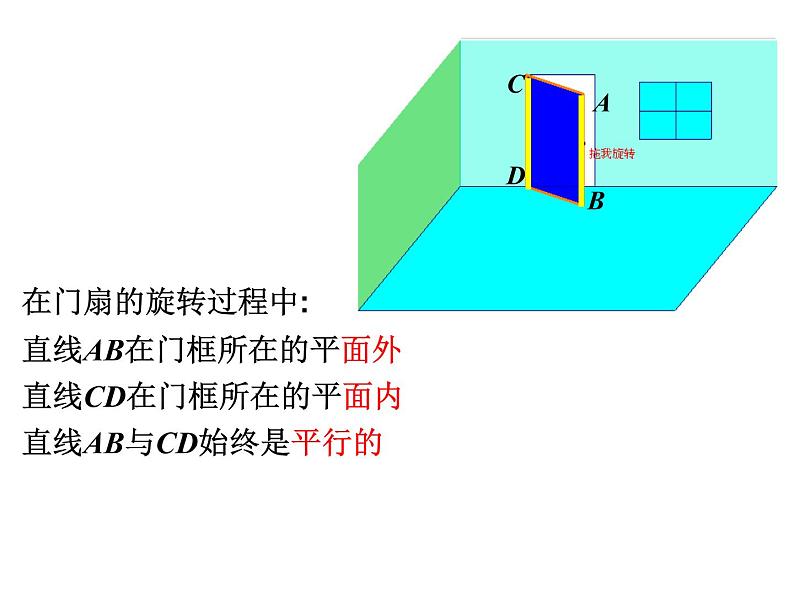
直线AB在门框所在的平面外
直线CD在门框所在的平面内
直线AB与CD始终是平行的
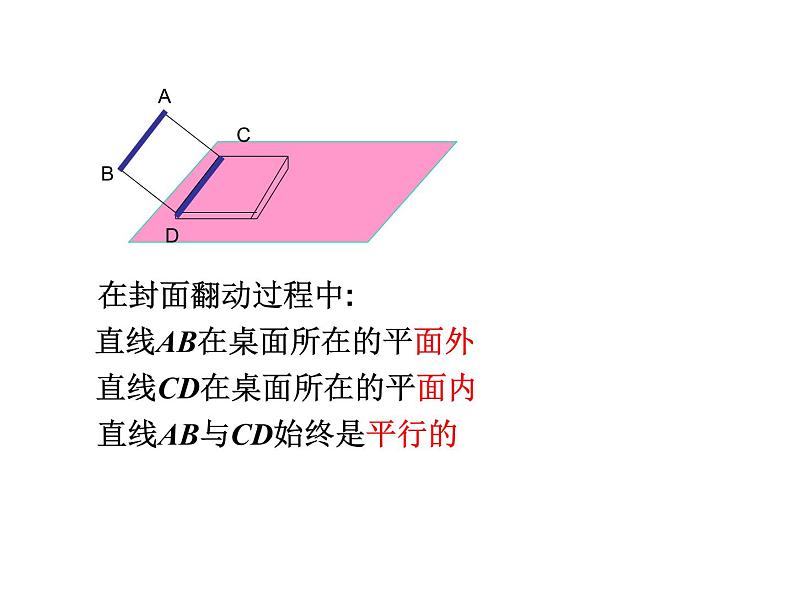
直线AB在桌面所在的平面外
直线CD在桌面所在的平面内
下图中的直线 a 与平面α平行吗？
（1）这两条直线共面吗？
如果平面外的一条直线和此平面内的一条直线平行，那么这条直线和这个平面平行.
直线和平面平行的判定定理：
六、讨论： 判断下列命题是否正确。（1）（2）（3）
七、理论提升（1）判定定理的三个条件缺一不可
简记为：线线平行则线面平行
如图，长方体 中，
（1）与AB平行的平面是 ；
（2）与 平行的平面是 ；
（3）与AD平行的平面是 ；
例1 已知：空间四边形ABCD 中，E，F 分别AB，AD 的中点。
求证：EF//平面BCD．
分析：EF在面BCD外，要证明EF∥面BCD，只要证明EF和面BCD内一条直线平行即可。EF和面BCD哪一条直线平行呢？连结BD立刻就清楚了。
例1 已知：空间四边形ABCD 中，E，F分别是 AB，AD 的中点． 求证：EF//平面BCD．
因为E，F分别是AB，AD 的中点,所以EF//BD
小结：在平面内找(作)一条直线与平面外的直线平行时可以通过 三角形的中位线、梯形的中位线、平行线的性质等来完成。
如图，四棱锥A-DBCE中，O为底面正方形DBCE对角线的交点，F为AE的中点. 求证: AB//平面DCF.
例2 如图，四面体ABCD中，E，F，G，H分别是AB，BC，CD，AD的中点.
(3)你能说出图中满足线面平行位置 关系的所有情况吗？
(1)E、F、G、H四点是否共面？
(2)试判断AC与平面EFGH的位置关系；
解：(1)E、F、G、H四点共面。
∵在△ABD中，E、H分别是AB、AD的中点.
EH ∥GF且EH＝GF
∴E、F、G、H四点共面。
（2） AC ∥平面EFGH
（3）由EF ∥HG ∥AC，得
由BD ∥EH ∥FG，得
______________.
1. 如图，在空间四边形ABCD中，E、F 分别为AB、AD上的点，若 ，则EF与平面BCD的位置关系是
利用平行线定理证线线平行.
解：连接BD交AC于点O,
1．证明直线与平面平行的方法：
2．数学思想方法：转化的思想
作业：课本P34 A组第4题；B组第1题