圆的基本元素PPT课件免费下载

华师大版初中数学九年级下册课文《圆的基本元素》,完整版PPT课件免费下载，优秀PPT背景图搭配，精美的免费ppt模板。轻松备课，欢迎免费下载使用。

圆的定义与圆有关的概念同圆的半径相等

一、【课程的主要内容】

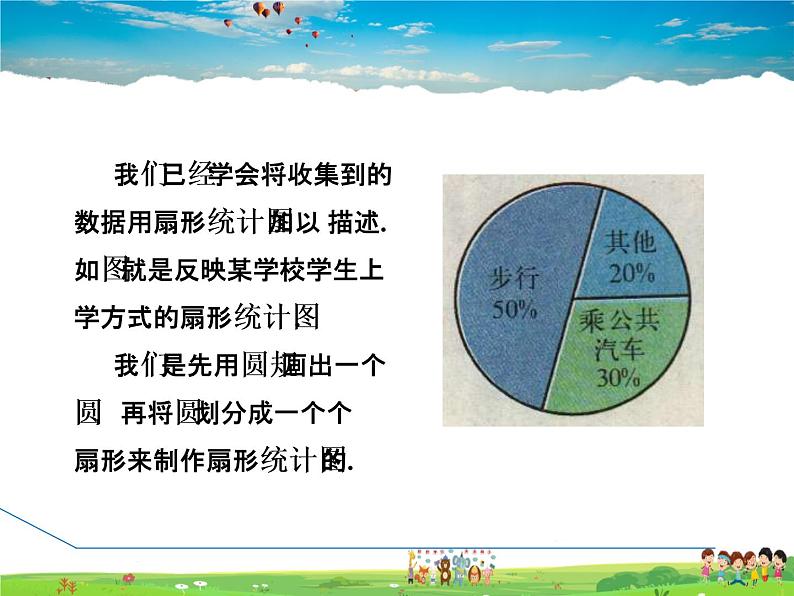
我们已经学会将收集到的数据用扇形统计图加以 描述.如图就是反映某学校学生上学方式的扇形统计图. 我们是先用圆规画出一个圆，再将圆划分成一个个扇形来制作扇形统计图的.
圆的定义：(1)描述性定义：在一个平面内，线段OA 绕它固定的一个 端点O旋转一周，另一个端点A所形成的图形叫做圆． 其固定的端点O叫做圆心，线段OA叫做半径．(2)集合观点定义：圆也可以看成是所有到定点(圆心)的距 离等于定长(半径)的点的集合．
要点精析：(1)确定一个圆需要两个要素，一是圆心，二是半径．圆 心定其位置，半径定其大小．(2)圆是一条封闭的曲线，曲线是“圆周”，而不能认为是 “圆面”．(3)“圆上的点”指圆周上的点．
下列说法中，错误的有( )(1)经过点P的圆有无数个；(2)以点P为圆心的圆有无数个；(3)半径为3 cm且经过点P的圆有无数个；(4)以点P为圆心，3 cm为半径的圆有无数个． A．1个 B．2个 C．3个 D．4个
确定一个圆必须有两个条件，即圆心和半径，只满足一个条件或不满足任何一个条件的圆都有无数个，由此可知(1)(2)正确；(3)半径确定，但圆心不确定，仍有无数个圆；(4)圆心和半径都确定的圆有且只有一个(唯一)．
1.圆的两种定义中确定圆的条件是相同的，即圆心和半径，两者缺一不可；2.“点在圆上”和“圆过点”表示的意义都是：这个点在圆周上；3. 圆将平面划分为三部分：圆上、圆内、圆外.
下列关于圆的叙述中正确的是( )A．圆是由圆心唯一确定的B．圆是一条封闭的曲线C．到定点的距离小于或等于定长的所有点组成圆D．圆内任意一点到圆心的距离都相等平面内已知点P，以P为圆心，3 cm为半径作圆，这样的圆可以作( )A．1个 B．2个 C．3个 D．无数个
在平面直角坐标系中，⊙O的圆心在原点，半径为2，则下面各点在⊙O上的是( )A．(1，1) B．(－1， )C．(－2，－1) D．( ，－2)
1．与圆有关的概念：(1)弦与直径： 弦：连结圆上任意两点的线段叫做弦(如图中的CD和AB)． 直径：经过圆心的弦叫做直径(如图中的AB)，且直径等于 半径(OA，OB)的2倍. 直径是圆中最长的弦． 注意：弦与直径间的关系：直径是过圆心的弦，因此直径 是弦，但弦不一定是直径；在提到“弦”时，如果没有特别 说明，不要忘记直径这种特殊的弦．
(2)弧、半圆、优弧、劣弧： 圆上任意两点间的部分叫做圆弧，简称弧. 圆的任意一 条直径的两个端点把圆分成两条弧, 每一条弧都叫做半 圆. 小于半圆周的弧叫做劣弧(如图中的 )，大于半 圆周的弧叫做优弧(如图中的 )．劣弧用“⌒”和弧 两端的字母表示；优弧用“⌒ ”和三个字母(弧两端的字 母和弧中间的任一字母)表示. 弧分为优弧、半圆、劣弧． 注意：半圆是弧，但弧不一定是半圆．
(3)等圆与等弧： 能够重合的两个圆叫做等圆．所以半径相等的两个圆是 等圆． 在同圆或等圆中，能够互相重合的弧叫做等弧．(4)圆心角：顶点在圆心的角叫做圆心角．2．弦与弧之间的关系：(1)弦是圆上两点间的线段，有无数条；弧是圆上两点间的 部分，弧是曲线，弧也有无数条．(2)每条弧对一条弦；而每条弦所对的弧有两条：优弧、劣 弧或两个半圆．

二、【拓展学习】

3．易错警示：(1)只有同圆或等圆中才可能有等弧，等弧长度一定相等， 但长度相等的弧不一定是等弧． 弧不仅有长度，还有度数，规定半圆的度数为180°， 劣弧的度数小于180°，优弧的度数大于180°.(2)半径不变，圆心变产生等圆；圆心不变，半径变产生 同心圆．
下列语句中正确的有（ ）①直径是弦；②弦是直径；③半径相等的两个半圆是等弧；④长度相等的两条弧是等弧；⑤半圆是弧，弧不一定是半圆.A. 1 个 B. 2 个 C. 3 个 D. 4 个
直径是最长的弦，故①正确；直径是过圆心的弦，但弦不一定是直径，故②错误；半圆是弧，半径相等的两个半圆能互相重合，所以是等弧，故③正确；只有在同圆或等圆中，长度相等的两条弧才是等弧，故④错误；弧分为劣弧、优弧、半圆，故⑤正确.
只有同圆或等圆中才可能有等弧，等弧长度一定相等，但长度相等的弧不一定是等弧.弧不仅有长度，还有度数，规定：半圆的度数为180 °，劣弧的度数小于180°，优弧的度数大于180° .
如图所示 ，已知⊙O上有A，B，C三个点，以其中两个点为端点的弧共有________条，弦共有________条．
由弧的概念知以A，B，C中任意两个点为端点的弧有 共6条；由弦的概念知以A，B，C中任意两个点为端点的弦有AB，BC，AC，共3条．
圆上的任意两点分圆为两条弧： 一条优弧、一条劣弧或两个半圆，本题容易忽视圆中的优弧而造成得到3条弧的错误答案；在同圆中每段弧对应一条弦，而每条弦对应两条弧：一条优弧、一条劣弧或两个半圆．

三、【课堂练习】

下列说法中，正确的是( )①弦是直径；②半圆是弧；③过圆心的线段是直径；④半圆是最长的弧；⑤直径是圆中最长的弦．A．②③ B．③⑤ C．④⑤ D．②⑤
如图，点A，B，C在⊙O上，点O在线段AC上，点D在线段AB上，下列说法正确的是( )A．线段AB，AC，CD，OB都是弦B．与线段OB相等的线段有OA，OC，CDC．图中的优弧有2条D．AC是弦，AC又是⊙O的直径，所以弦是直径
下列说法中，错误的是( )A．直径相等的两个圆是等圆B．长度相等的两条弧是等弧C．圆中最长的弦是直径D．一条弦把圆分成两条弧，这两条弧可能相等
圆的特性：(1)圆上各点到定点(圆心O)的距离都等于定长(半径r)， 即同圆的半径相等．(2)到定点O的距离等于定长r的点都在同一个圆上，即 到圆心的距离等于半径的点在圆上．
[ 中考· 益阳]如图所示， 分别以A，B 为圆心， 线段AB 的长为半径的两个圆相交于C，D 两点，则∠ CAD 的度数为 .
本题考查了等圆的半径相等、等边三角形的定义和性质，构造同圆的半径是解题关键.
如图所示，连结BC，BD.∴ AC=AD=AB=BD=BC.∴△ ABC 和△ ABD 都是等边三角形.∴∠ BAC= ∠ BAD=60°.∴∠ CAD=120°.
利用特殊图形：平角、等边三角形、含30°角的直角三角形、等腰直角三角形等求角度，是没有已知角度求角度问题的一种常用方法.
如图，点A，D，G，M在半圆O上，四边形ABOC，四边形OFDE，四边形HMNO都是矩形，设BC＝a，EF＝b，NH＝c，则下列各式正确的是( )A．a>b>c B．a＝b＝c C．c>a>b D．b>c>a
(2015·绍兴)如图，已知点A(0，1)，B(0，－1)，以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则∠BAC等于________度．