初中数学华师大版九年级下册第27章 圆27.1 圆的认识3. 圆周角教学课件ppt

这是一份初中数学华师大版九年级下册第27章 圆27.1 圆的认识3. 圆周角教学课件ppt，共26页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，圆周角的定义，圆周角和圆心角的关系等内容，欢迎下载使用。
圆周角的定义圆周角和圆心角的关系同弧或等弧所对的圆周角
顶点在圆上，两边分别与圆还有另一个交点的角叫做圆周角．特征：①角的顶点在圆上；②角的两边都与圆相交，这两个特征是判定圆周角不 可缺少的条件．
如图，下列各角是圆周角的是(　　)A．∠AOD　　　　　B. ∠AOCC. ∠BAD D. ∠BOD
可根据圆周角的定义进行判断，显然∠AOD，∠AOC，∠BOD均是圆心角，只有∠BAD符合圆周角的两个特征．
判断一个角是否为圆周角，关键是看这个角是否具备圆周角的两个特征：(1)角的顶点在圆上；(2)角的两边都与圆相交，二者缺一不可．
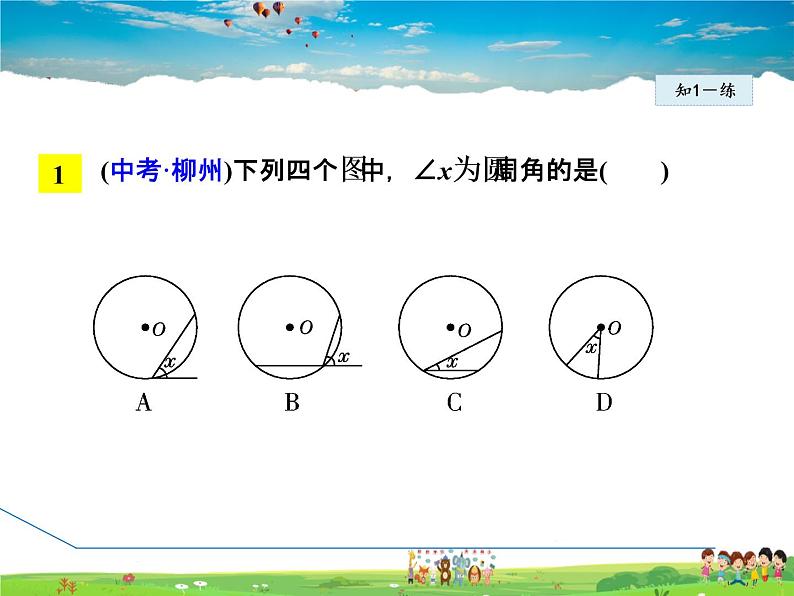
(中考·柳州)下列四个图中，∠x为圆周角的是(　　)
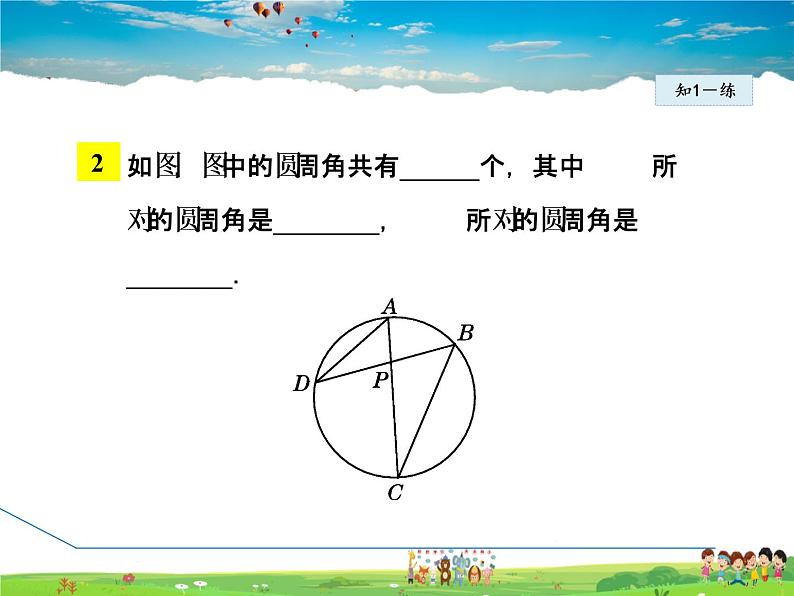
如图，图中的圆周角共有______个，其中 所对的圆周角是________， 所对的圆周角是________．
1. 在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于 该弧所对的圆心角的一半；相等的圆周角所对的弧相等． 拓展：在圆中解决相关问题时，常常进行以下三种转化：(1)利用“同弧或等弧所对的圆周角等于它所对的圆心角的一半”， 实现圆周角与圆心角之间的转化；(2)利用“同弧或等弧所对的圆周角相等”，实现相等圆周角之间 的转化；(3)利用在“同圆或等圆中，相等的圆周角所对的弧相等”，实现 弧相等或线段相等的转化．
2. 易错提示：(1)圆周角与圆心角存在联系的前提条件是它们对着同一条弧或 等弧，若把“同弧或等弧”去掉，而简单地说成“圆周角等于 圆心角的一半”是错误的．(2)若将“同弧或等弧”改为“同弦或等弦”，则结论不成立，因为 一条弦所对的圆周角有两种可能，一般情况下是不相等的． 如图所示， ∠1与∠2都对着弦BD，但∠1≠∠2.(3)“相等的圆周角所对的弧相等”成立的前提条 件是“在同圆或等圆中”，缺少了此条件，结论是不成立的．
如图，A，B，C，D是同一圆上的点，∠1＝68°，∠A＝40°，则∠D＝________．
由圆周角定理可知∠C＝∠A＝40°，由三角形的外角性质得∠D＝∠1－∠C＝68°－40°＝28°.
本题应用转化思想，利用“同弧所对的圆周角相等”将已知角和要求的角转化为与同一个三角形有关的角，利用三角形的外角性质求解．
如图，在⊙O中，∠AOC＝150°，求∠ABC，∠ADC，∠EBC的度数，并判断∠ABC和∠ADC，∠EBC和∠ADC之间的度数关系．
解题的关键是分清同弧所对的圆心角和圆周角，如所对的圆心角是∠AOC，所对的圆周角是∠ABC，所对的圆心角是大于平角的∠α，所对的圆周角是∠ADC.
∵∠AOC＝150°，∴∠ABC＝ ∠AOC＝75°.∴∠EBC＝180°－∠ABC＝180°－75°＝105°，∵∠α＝360°－∠AOC＝360°－150°＝210°，∴∠ADC＝ ∠α＝105°.∴∠EBC＝∠ADC，即∠EBC与∠ADC相等．又∵∠ABC＋∠ADC＝75°＋105°＝180°，∴∠ABC和∠ADC互补．
(2015·张家界)将量角器按如图所示的方式放置在三角形纸板上，使顶点C在半圆上，点A，B的读数分别为100°，150°，则∠ACB＝________．
(2016·绍兴)如图，BD是⊙O的直径，点A，C在⊙O上， ，∠AOB＝60°，则∠BDC的度数是(　　)A．60° B．45° C．35° D．30°
(2015·珠海)如图，在⊙O中，直径CD垂直于弦AB，若∠C＝25°，则∠BOD的度数是(　　)A．25° B．30° C．40° D．50°
同弧或等弧所对的圆周角
〈广州〉如图，在⊙O中，∠ACB＝∠BDC＝60°， AC＝2 cm. (1)求∠BAC的度数； (2)求⊙O的周长．
(1)观察图形发现∠BAC与∠BDC为同弧所对的圆周角，故∠BAC＝∠BDC＝60°；(2)要求圆的周长，必须先求出半径，可利用垂径定理，即连结OA，作OE⊥AC于点E，构造直角三角形求出半径．
(1)在⊙O中，∠BDC与∠BAC均为 所对的圆周角， ∴∠BAC＝∠BDC＝60°.(2)∵∠ACB＝60°，∠BAC＝60°， ∴△ABC为等边三角形． 连结OA，作OE⊥AC于点E，如图. ∵OE⊥AC，AC＝2 cm，∴AE＝ cm. 在Rt△AOE中，∠AOE＝∠ABC＝60°，∴∠OAE＝30°， ∴OE＝ OA，又∵OE2＋AE2＝OA2，∴OA＝2 cm， ∴⊙O的周长为2π×2＝4π(cm)．
巧用圆周角定理可以帮助我们找出题目中隐藏的角相等关系，我们在做题时要善于观察图形，看图形具备哪些定理的基本图形的特征，找出相关的相等线段或角．
(2016·自贡)如图，在⊙O中，弦AB与CD交于点M，∠A＝45°，∠AMD＝75°，则∠B的度数是(　　)A．15° B．25°　 C．30°　 D．75°
(2016·达州)如图，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，则tan∠OBC为(　　)A. B． C. D.
(2015·莆田)如图，在⊙O中， ，∠AOB＝50°，则∠ADC的度数是(　　)A．50° B．40° C．30° D．25°
在同圆或等圆中，在圆心角、圆周角、弦、弧这四组量中，如果其中一组量相等，那么其余的三组量也分别相等．注意：其中的“等弦对等圆周角”，必须是弦的同侧的圆周角．