中考数学总复习精炼（含答案）：07图形的变化

这是一份中考数学总复习精炼（含答案）：07图形的变化，共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


一、选择题(每小题3分，共30分)
1.下面四大国产手机品牌图标中，是轴对称图形的是( A )
2.在平面直角坐标系内，线段CD是由线段AB平移得到的，点A(－2,3)的对应点为C(1,4)，则点B(－4，－1)的对应点D的坐标为( D )
A.(－7，－2) B.(4,2) C.(0,1) D.(－1,0)
3.若a∶b＝3∶4，且a＋b＝14，则2a－b的值是( A )
A.4 B.2 C.20 D.14
4.菱形不具备的性质是( D )
A.是轴对称图形 B.是中心对称图形
C.对角线互相垂直 D.对角线一定相等
5.如图，有一斜坡AB，坡顶B离地面的高度BC为30 m，斜坡的倾斜角是∠BAC，若tan∠BAC＝eq \f(2,5)，则此斜坡的水平距离AC为( A )
A.75 m B.50 m C.30 m D.12 m
6.在平面直角坐标系中，点P(－3，m2＋1)关于原点对称点在( D )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
7.如图，在矩形ABCD中，AB＝6，AD＝3，动点P满足S△PAB＝eq \f(1,3)S矩形ABCD，则点P到A，B两点距离之和PA＋PB的最小值为( A )
A.2eq \r(13) B.2eq \r(10) C.3eq \r(5) D.eq \r(41)
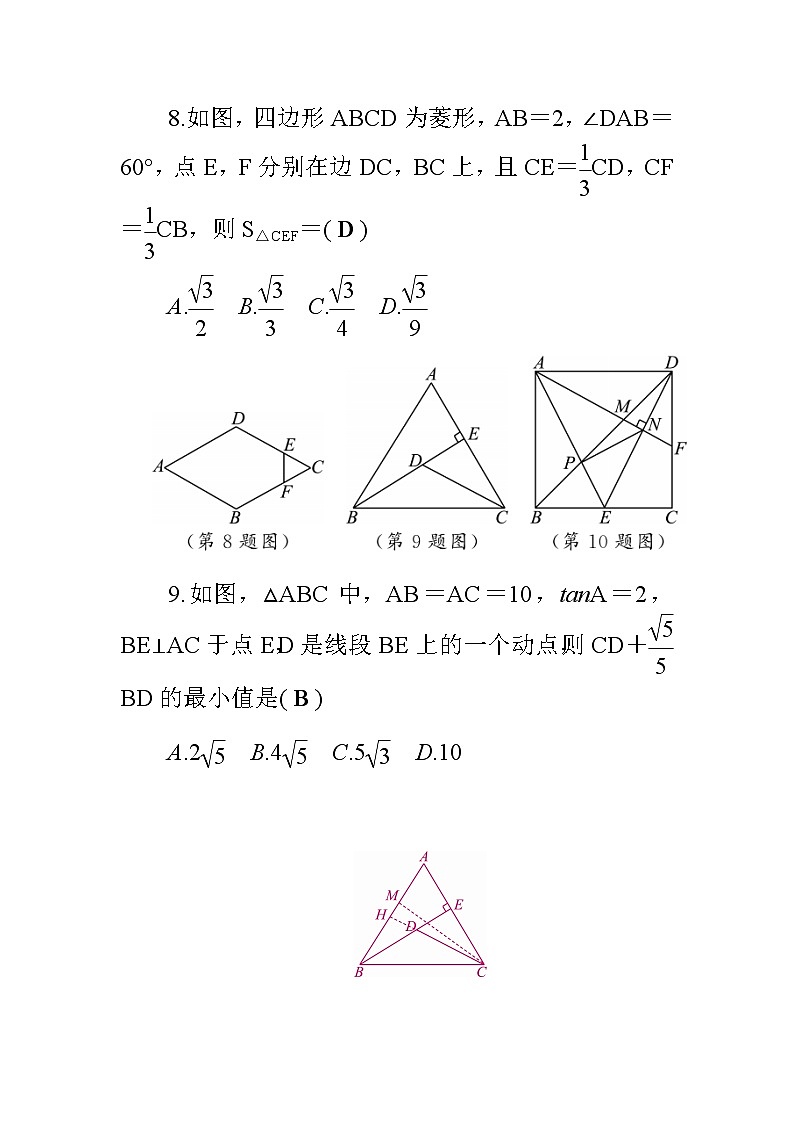
8.如图，四边形ABCD为菱形，AB＝2，∠DAB＝60°，点E，F分别在边DC，BC上，且CE＝eq \f(1,3)CD，CF＝eq \f(1,3)CB，则S△CEF＝( D )
A.eq \f(\r(3),2) B.eq \f(\r(3),3) C.eq \f(\r(3),4) D.eq \f(\r(3),9)
9.如图，△ABC中，AB＝AC＝10，tanA＝2，BE⊥AC于点E，D是线段BE上的一个动点，则CD＋eq \f(\r(5),5)BD的最小值是( B )
A.2eq \r(5) B.4eq \r(5) C.5eq \r(3) D.10
解析：如图，作DH⊥AB于H，CM⊥AB于M.可求出AE＝2eq \r(5)，∴BE＝4eq \r(5)，∵AB＝AC，BE⊥AC，CM⊥AB，∴CM＝BE＝4eq \r(5)(等腰三角形两腰上的高相等)，∵∠DBH＝∠ABE，∠BHD＝∠BEA，∴sin∠DBH＝eq \f(DH,BD)＝eq \f(AE,AB)＝eq \f(\r(5),5)，∴DH＝eq \f(\r(5),5)BD，
∴CD＋eq \f(\r(5),5)BD＝CD＋DH，∴CD＋DH≥CM，
∴CD＋eq \f(\r(5),5)BD≥4eq \r(5)，∴CD＋eq \f(\r(5),5)BD的最小值为4eq \r(5).
10.如图，正方形ABCD的边长为2，点E是BC的中点，AE与BD交于点P，F是CD上一点，连接AF分别交BD，DE于点M，N，且AF⊥DE，连接PN，则以下结论中：①S△ABM＝4S△FDM；②PN＝eq \f(2\r(65),15)；③tan∠EAF＝eq \f(3,4)；④△PMN∽△DPE，正确的是( A )
A.①②③ B.①②④ C.①③④ D.②③④
解析：证△ADF≌△DCE(ASA)，∴DF＝CE＝1，∵AB∥DF，∴△ABM∽△FDM，∴eq \f(S△ABM,S△FDM)＝(eq \f(AB,DF))2＝4，∴S△ABM＝4S△FDM；故①正确；可求出EN＝eq \f(3\r(5),5)，
AN＝eq \r(AD2－DN2)＝eq \f(4\r(5),5)，∴tan∠EAF＝eq \f(EN,AN)＝eq \f(3,4)，故③正确，作PH⊥AN于H.可求出AH＝eq \f(2,3)×eq \f(4\r(5),5)＝eq \f(8\r(5),15)，HN＝eq \f(4\r(5),15)，∴PN＝eq \r(PH2＋NH2)＝eq \f(2\r(65),15)，故②正确，∵PN≠DN，∴∠DPN≠∠PDE，∴△PMN与△DPE不相似，故④错误.
二、填空题(每小题4分，共24分)
11.下面摆放的图案，从第2个起，每一个都是前一个按顺时针方向旋转90°得到，第2019个图案与第1个至第4个中的第 3 个箭头方向相同(填序号).
12.在平面直角坐标系中，点M(a，b)与点N(3，－1)关于x轴对称，则a＋b的值是 4 .
13.如图，在△ABC中，sinB＝eq \f(1,3)，tanC＝eq \f(\r(2),2)，AB＝3，则AC的长为 eq \r(3) .
14.已知正方形ABCD的面积是2，E为正方形一边BC在从B到C方向的延长线上的一点，若CE＝eq \r(2)，连接AE，与正方形另外一边CD交于点F，连接BF并延长，与线段DE交于点G，则BG的长为 eq \f(2\r(10),3) .
15.如果三角形有一边上的中线长等于这边的长，那么称这个三角形为“好玩三角形”.若Rt△ABC是“好玩三角形”，且∠A＝90°，则tan∠ABC＝ eq \f(\r(3),2)或eq \f(2\r(3),3) .
16.如图，已知⊙O的半径为1，AB，AC是⊙O的两条弦，且AB＝AC，延长BO交AC于点D，连接OA，OC，若AD2＝AB·DC，则OD＝ eq \f(\r(5)－1,2) .
解析：可证△ADO∽△BDA，∴eq \f(AD,BD)＝eq \f(OD,AD)＝eq \f(AO,AB)，设OD＝x，则BD＝1＋x，∴eq \f(AD,1＋x)＝eq \f(x,AD)＝eq \f(1,AB)，
∴AD＝eq \r(x(x＋1))，AB＝eq \f(\r(x(x＋1)),x)，
∵DC＝AC－AD＝AB－AD，
AD2＝AB×DC，(eq \r(x(x＋1)))2＝eq \f(\r(x(x＋1)),x)(eq \f(\r(x(x＋1)),x)－eq \r(x(x＋1)))，整理得：x2＋x－1＝0，解得：x＝eq \f(－1＋\r(5),2)或x＝eq \f(－1－\r(5),2)(舍去)，因此OD＝eq \f(\r(5)－1,2).
三、解答题(共66分)
17.(6分)如图，将△ABC绕点C顺时针旋转90°得到△EDC.若点A，D，E在同一条直线上，且∠ACB＝20°，求∠CAE及∠B的度数.
解：根据旋转的性质可知CA＝CE，
且∠ACE＝90°，所以△ACE是等腰直角三角形.
所以∠CAE＝45°；根据旋转的性质可得∠BCD＝90°，∵∠ACB＝20°.∴∠ACD＝70°.∴∠EDC＝45°＋70°＝115°.所以∠B＝∠EDC＝115°.
18.(8分)如图，在网格中，每个小正方形的边长均为1个单位长度.我们将小正方形的顶点叫做格点，△ABC的三个顶点均在格点上.
(1)将△ABC先向右平移6个单位长度，再向上平移3个单位长度，得到△A1B1C1，画出平移后的△A1B1C1；
(2)建立适当的平面直角坐标系，使得点A的坐标为(－4,3)；
(3)在(2)的条件下，直接写出点A1的坐标.

解：(1)如图，△A1B1C1为所作； (2)如图； (3)点A1的坐标为(2,6).
19.(8分)如图，AB，CD为两个建筑物，建筑物AB的高度为15 m，从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°，测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间的水平距离BD的长度；(2)求建筑物CD的高度(结果保留根号).

解：(1)根据题意得∠ADB＝∠EAD＝45°，
在Rt△ABD中，∴∠BAD＝∠ADB＝45°，
∴BD＝AB＝15(米)；
(2)延长DC交AE于点F，根据题意可知四边形ABDF是正方形，∴AF＝BD＝DF＝15，
在Rt△AFC中，∵∠FAC＝30°，
∴CF＝AFtan∠CAF＝15tan30°＝5eq \r(3)，
∵DF＝15，∴CD＝15－5eq \r(3).
20.(10分)如图，在矩形ABCD中，AB＝6，BC＝10，将矩形沿直线EF折叠，使得点A恰好落在边BC上，记此点为G，点E和点F分别在边AB和边AD上.
(1)当BG＝3eq \r(2)时，求AE的长；
(2)在矩形翻折中，是否存在FG＝CG？若存在，请求出FG的长，若不存在，请说明理由.

解：(1)由折叠易知：AE＝EG，设AE＝EG＝x，则有BE＝6－x，∴由勾股定理易得：x2＝(6－x)2＋(3eq \r(2))2，解得：x＝eq \f(9,2)，即：AE＝eq \f(9,2)；
(2)如图，过F作FH⊥CG于H，连接FC，当FG＝GC时，则有：AF＝FG＝GC＝x，CH＝DF＝10－x；∴GH＝x－(10－x)＝2x－10，在Rt△FGH中，
由勾股定理易得：x2＝62＋(2x－10)2，化简得：
3x2－40x＋136＝0，∵Δ＝(－40)2－4×3×136＝－32＜0，∴此方程没有实数根.故不存在FG＝GC.
21.(10分)如图，一副直角三角板△ABC和△DEF，∠F＝30°.将△ABC和△DEF放置如图2的位置，点B，D，C，F在同一直线上.
(1)如图3，△ABC固定不动，△DEF绕点D逆时针旋转30°时，判断BC与EF的位置关系，并说明理由.
(2)在图2的位置上，△DEF绕点D逆时针旋转α(0＜α＜180°)，在旋转过程中，两个三角形的边是否存在垂直关系？若存在直接写出旋转的角度，并写出哪两边垂直；若不存在，请说明理由.
解：(1)BC∥EF，理由如下：∵△DEF绕点D逆时针旋转30°，∴∠FDC＝30°，∴∠FDC＝∠F＝30°，∴BC∥EF；
(2)当α＝45°时，∴∠C＋∠FDC＝90°，
∠B＋∠EDB＝90°，∴DF⊥AC，DE⊥AB；
当α＝75°时，EF⊥AC；当α＝90°时，DF⊥BC；
当α＝120°时，EF⊥BC；当α＝135°时，DE⊥AC，DF⊥AB.
22.(12分)如图，已知AC，AD是⊙O的两条割线，AC与⊙O交于B，C两点，AD过圆心O且与⊙O交于E，D两点，OB平分∠AOC.
(1)求证：△ACD∽△ABO；
(2)过点E的切线交AC于F，若EF∥OC，OC＝3，求EF的值.

证明：(1)∵OB平分∠AOC，∴∠BOE＝eq \f(1,2)∠AOC，又∵∠D＝eq \f(1,2)∠AOC，∴∠D＝∠BOE，且∠A＝∠A，∴△ACD∽△ABO；
(2)∵EF切⊙O于E，∴∠OEF＝90°，∵EF∥OC，∴∠DOC＝∠OEF＝90°，∵OC＝OD＝3，
∴CD＝eq \r(OC2＋OD2)＝3eq \r(2)，∵△ACD∽△ABO，∴eq \f(AD,AO)＝eq \f(CD,BO)，∴eq \f(AE＋6,AE＋3)＝eq \f(3\r(2),3)，∴AE＝3eq \r(2)，∵EF∥OC，∴eq \f(AE,AO)＝eq \f(EF,OC)，∴eq \f(3\r(2),3\r(2)＋3)＝eq \f(EF,3)，
∴EF＝6－3eq \r(2).
23.(12分)如图，在△ABC中，∠A＝90°，AB＝3，AC＝4，点M，Q分别是边AB，BC上的动点(点M不与A，B重合)，且MQ⊥BC，过点M作BC的平行线MN，交AC于点N，连接NQ，设BQ为x.
(1)试说明不论x为何值时，总有△QBM∽△ABC；
(2)是否存在一点Q，使得四边形BMNQ为平行四边形，试说明理由；
(3)当x为何值时，四边形BMNQ的面积最大，并求出最大值.
解：(1)∵MQ⊥BC，∴∠MQB＝90°，
∴∠MQB＝∠CAB，又∠QBM＝∠ABC，∴△QBM∽△ABC；
(2)当BQ＝MN时，四边形BMNQ为平行四边形，∵MN∥BQ，BQ＝MN，∴四边形BMNQ为平行四边形；
(3)∵∠A＝90°，AB＝3，AC＝4，
∴BC＝eq \r(AB2＋AC2)＝5，∵△QBM∽△ABC，
∴eq \f(QB,AB)＝eq \f(QM,AC)＝eq \f(BM,BC)，即eq \f(x,3)＝eq \f(QM,4)＝eq \f(BM,5)，解得，QM＝eq \f(4,3)x，BM＝eq \f(5,3)x，∵MN∥BC，∴eq \f(MN,BC)＝eq \f(AM,AB)，即eq \f(MN,5)＝eq \f(3－\f(5,3)x,3)，解得，MN＝5－eq \f(25,9)x，则四边形BMNQ的面积＝eq \f(1,2)×(5－eq \f(25,9)x＋x)×eq \f(4,3)x＝－eq \f(32,27)(x－eq \f(45,32))2＋eq \f(75,32)，∴当x＝eq \f(45,32)时，
四边形BMNQ的面积最大，最大值为eq \f(75,32).