切线PPT课件免费下载

华师大版初中数学九年级下册课文《切线》,完整版PPT课件免费下载，优秀PPT背景图搭配，精美的免费ppt模板。轻松备课，欢迎免费下载使用。

一、【课程的主要内容】

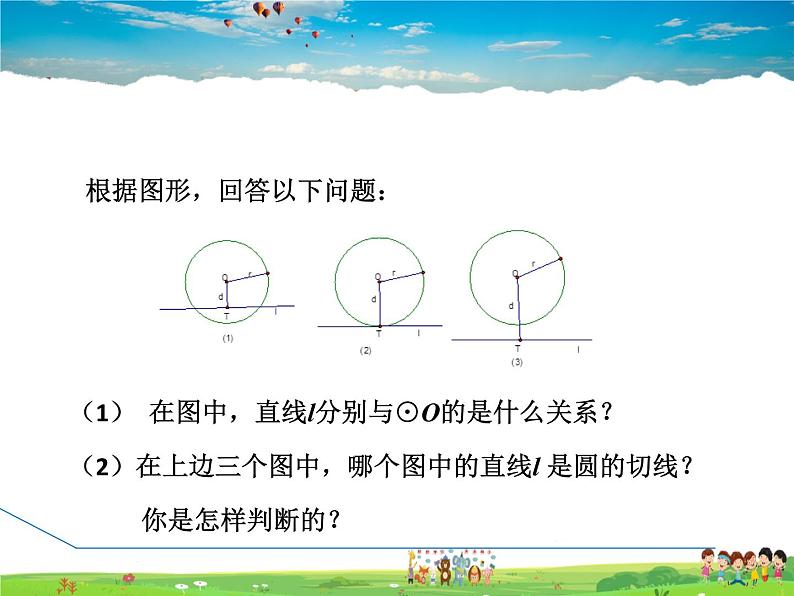
根据图形，回答以下问题：
（1） 在图中，直线l分别与⊙O的是什么关系？（2）在上边三个图中，哪个图中的直线l 是圆的切线？ 你是怎样判断的？
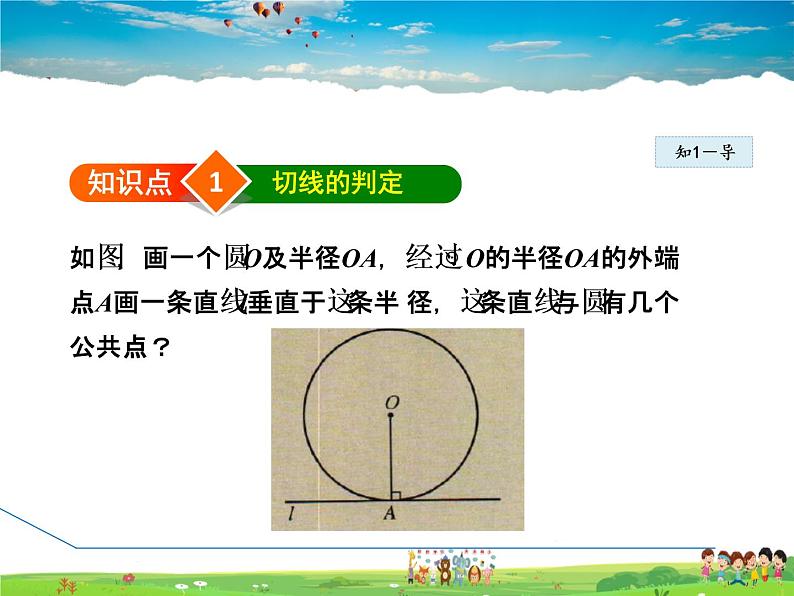
如图，画一个圆O及半径OA，经过⊙ O的半径OA的外端点A画一条直线l垂直于这条半 径，这条直线与圆有几个公共点？
从图可以看出，对直线l上除点A外的任一 点P，必有OP > OA，即点P立于圆外，从而可知直线与 圆只有一个公共点，所以直线l是圆的切线.
1. 判定定理：经过圆的半径的外端且垂直于这条半径的直 线是圆的切线． 要点精析：切线必须同时具备两个条件：(1)直线过半径的外端；(2)直线垂直于半径．2. 判定方法：(1)定义法：与圆有唯一公共点的直线是圆的切线； (2)数量法：圆心到直线的距离等于半径的直线是圆的切线；(3)判定定理：经过半径的外端并且垂直于这条半径的直线是 圆的切线．
3. 切线判定常用的证明方法：(1)有切点，连半径，证垂直： 如果已知直线经过圆上的一点，那么连结这点和圆心，得到 辅助半径，再证明所作半径与这条直线垂直即可，简记为： 有切点，连半径，证垂直．(2)无切点，作垂直，证半径： 如果已知条件中不知道直线与圆是否有公共点，那么过圆心 作直线的垂线段，再证明垂线段的长度等于半径即可，简记 为：无切点，作垂直，证半径．
(1)解答本题运用了连半径，证垂直．一定要分清圆的切线的判定定理的条件与结论，特别要注意“经过半径(或直径)的外端”和“垂直于这条半径(或直径)”这两个条件缺一不可，否则就不是圆的切线．(2)如果要证的切线过圆上某一点，那么连结这点和圆心(连半径)，证明该直线与过这点的半径垂直(证垂直)，即可判定直线与圆相切，这就是：连半径，证垂直．
如图，在Rt△ABC中，∠B＝90°，∠BAC的平分线交BC于点D，以点D为圆心，DB为半径作⊙D.求证：AC与⊙D相切．
直线AC是否与⊙D有公共点不确定，不能像上例那样“连半径，证垂直”，为此，过D点作DF⊥AC于点F，由d＝r⇒直线与圆相切可知，只需证DF＝DB即可．
如图，过点D作DF⊥AC于点F.∵∠B＝90°，∴DB⊥AB.又∵AD平分∠BAC，∴DF＝DB.∴AC与⊙D相切．
如果已知条件中不知道直线与圆是否有公共点，其证法是过圆心作直线的垂线段，再证明垂线段的长等于半径即可，简记为：作垂直，证半径．
如图，AB是⊙O的直径， ∠B = ∠ CAD, 求证：AC是⊙O的切线.
下列命题中，真命题是( )A．垂直于半径的直线是圆的切线B．经过半径外端的直线是圆的切线C．经过切点的直线是圆的切线D．圆心到某直线的距离等于半径，那么这条直线 是圆的切线
如图，△ABC是⊙O的内接三角形，下列选项中，能使过点A的直线EF与⊙O相切于点A的条件是( )A．∠EAB＝∠C B．∠B＝90°C．EF⊥AC D．AC是⊙O的直径
如图,如果直线l是⊙O的切线，点A为切点，那么半径OA与l垂直吗？

二、【拓展学习】

1. 性质定理：圆的切线垂直于经过切点的半径．要点精析：(1)性质定理的题设有两个条件： ①圆的切线；②半径过切点，应用时缺一不可．(2)切线的判定定理与性质定理的区别：切线的判定定理 是在未知相切而要证明相切的情况下使用，切线的性 质定理是在已知相切而要推得其他的结论时使用；它 们是一个互逆的过程，不要混淆．
2. 切线的性质：温故：(1)切线和圆只有一个公共点；(2)圆心到切线的距离等于半径；(3)圆的切线垂直于过切点的半径．知新：(推论)(4)经过圆心且垂直于切线的直线必过切点(找切点用)；(5)经过切点且垂直于切线的直线必过圆心(找圆心用)．以上(3)(4)(5)可归纳为：
已知直线满足：①过圆心；②过切点；③垂直于切线中的任意两个，就可得到第三个．拓展：(1)弦切角的定义：顶点在圆上，一边与圆相交(弦)，另 一边与圆相切(切线)的角叫做弦切角．(2)弦切角的性质：弦切角的度数等于它所夹弧所对的 圆周角的度数，亦等于它所夹弧的度数的一半，也 等于它所夹弧所对的圆心角度数的一半．
如图所示，AB 为⊙ O 的直径，PD 切⊙ O 于点C，交AB 的延长线于点D，且∠ D=2 ∠ CAD.（1）求∠ D 的度数.（2）若CD=2，求BD 的长.
（1）利用“等半径”得等腰三角形；（2）利用“切线”垂直于过切点的半径构成直角三角形，再结合相关性质求解.
已知圆的切线时，常连结圆心和切点，得到半径垂直于切线，通过构造直角三角形来解决问题，即“见切线，连半径，得垂线”；而等半径，可得等腰三角形，从而可得两底角相等；在同圆中有关切线的问题常通过等腰三角形和直角三角形的性质来解决问题.
(2015·吉林)如图，在⊙O中，AB为直径，BC为弦，CD为切线，连结OC.若∠BCD＝50°，则∠AOC的度数为( )A．40° B．50° C．80° D．100°
(2015·泸州)如图，PA，PB分别与⊙O相切于A，B两点，若∠C＝65°，则∠P的度数为( )A．65° B．130° C．50° D．100°
(2015·内江)如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD＝120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为( )A．40° B．35° C．30° D．45°

三、【课堂练习】

1.证明直线与圆相切有如下三种途径：(1)定义法：和圆有且只有一个公共点的直线是圆的 切线．(2)数量法(d＝r)：圆心到直线的距离等于半径的 直线是圆的切线．(3)判定定理：经过半径的外端并且垂直于这条半径 的直线是圆的切线．
2.作辅助线的两种方法：(1)若直线与圆的公共点未指明，则过圆心作直线的垂线段， 然后说明这条垂线段的长等于圆的半径；即“作垂直， 证半径”．(2)若直线与圆的一个公共点已指明，则连结这点和圆心， 说明直线垂直于经过这点的半径；即“连半径，证垂直”．3.切线的性质定理：圆的切线垂直于过且点的半径。4.已知直线满足：①过圆心；②过切点；③垂直于切线中的 任意两个，就可得到第三个．