专题强化（四）———函数零点问题学案

函数的零点

1. 零点的定义

  (1)函数f(x)的零点是使f(x)＝0的__    __.

(2)函数的零点、函数的图象、方程的根的关系．

2. 零点的存在性定理

  (1)条件：函数y＝f(x)在区间[a，b]上的图象是__    __，f(a)f(b)<0；

(2)函数y＝f(x)在区间(a，b)上有零点，即存在c∈(a，b)使f(c)＝0，这个c也就是f(x)＝0的根．

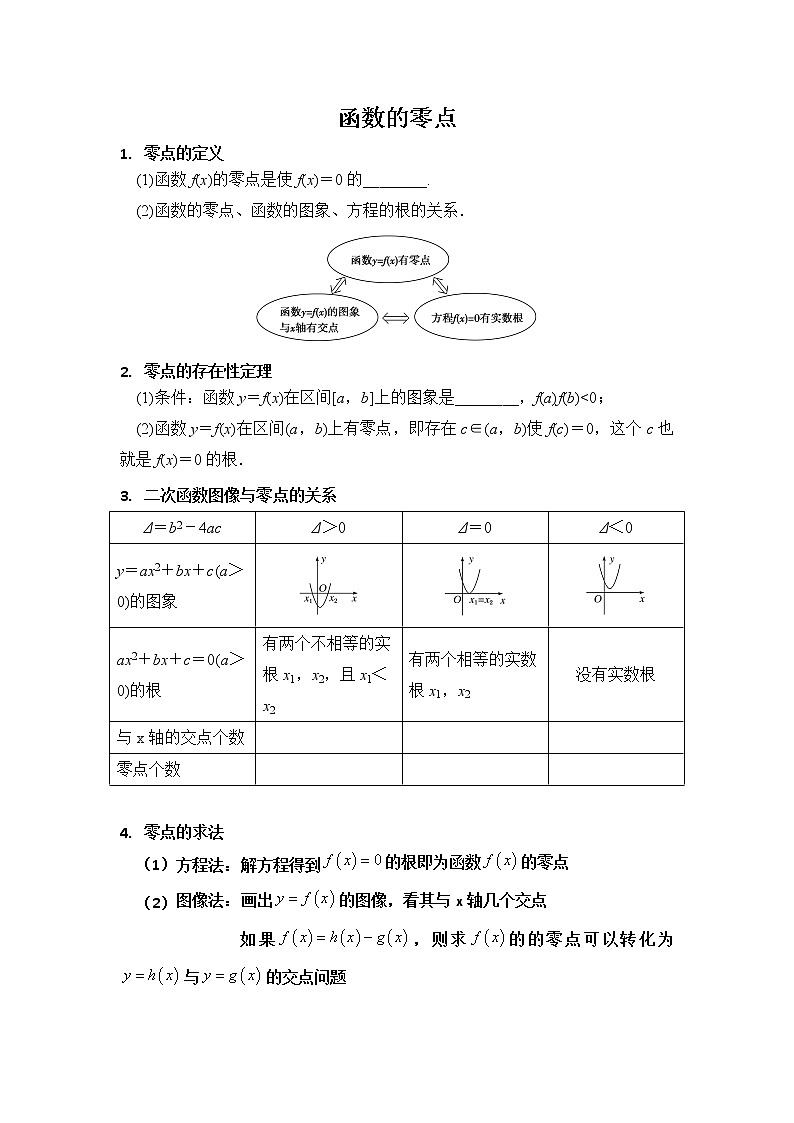
3. 二次函数图像与零点的关系

4. 零点的求法

（1）        方程法：解方程得到的根即为函数的零点

（2）        图像法：画出的图像，看其与x轴几个交点

               如果，则求的的零点可以转化为与的交点问题

经典例题

一．选择题（共12小题）

1．以下函数在区间上必有零点的是　　

A． B． C． D．

2．函数的零点个数为　　

A．0 B．1 C．2 D．3

3．函数的零点一定位于下列哪个区间　　

A． B． C． D．

4．已知定义在上的函数的图象是连续不断的，且有如下对应值表：那么函数一定存在零点的区间是　　

A． B． C． D．

5．已知函数，若方程有三个不同的实数根，则实数的取值范围为　　

A． B． C． D．

6．直线与函数的图象有4个交点，则的取值范围是　　

A． B． C． D．

7．已知用二分法求函数在内零点近似值的过程中发现，（1），，，则可以确定方程的根所在区间为　　

A． B． C． D．无法确定

8．函数的零点的大致区间为　　

A． B． C． D．

9．已知函数，在下列区间中，包含零点的区间是　　

A． B． C． D．

10．已知函数，若恰有两个零点，则的取值范围是　　

A．，，B．，，C．，， D．，

11．已知函数，，的零点依次为，，，则以下大小关系正确的是　　

A． B． C． D．

二．解答题（共2小题）

13．已知函数为常数）是奇函数．

（1）求的值；

（2）函数，若函数有零点，求参数的取值范围．

14．已知函数．

（1）当时，解不等式；

（2）设，，且函数存在零点，求实数的取值范围．

参考答案

一．选择题（共12小题）

1．【解答】解：根据题意，依次分析选项：

对于，，在区间有恒成立，在区间上没有零点，不符合题意，

对于，，在区间有恒成立，在区间上没有零点，不符合题意，

对于，，当时，，区间上有零点，符合题意，

对于，，在区间有恒成立，在区间上没有零点，不符合题意，

故选：．

2．【解答】解：函数的零点，就是的根，解方程可得．

方程无解，所以函数的零点个数为0．

故选：．

3．【解答】解：函数是连续函数，

（2），，

可得（2），

由零点判断定理可知函数的零点在，．

故选：．

4．【解答】解：由题意可知：（3），

（2），

所以（2）（3）．

函数一定存在零点的区间是

故选：．

5．【解答】解：画出函数的图象，如图示：

，

方程有三个不同的实数根，

即和的图象有3个不同的交点，

结合图象：，

故选：．

6．【解答】解：原问题等价于函数 与函数有4个交点，绘制函数图象如图所示，

由于函数在 处取得最小值，

故，解得：．

故选：．

7．【解答】解：由题意，，，

可得，

所以确定方程的根所在区间为：．

故选：．

8．【解答】解：函数是单调增函数，

（1），

，

所以（1）．

函数的零点的大致区间为

故选：．

9．【解答】解：函数是单调减函数，（2），（4），

所以，（2）（4），

所以函数的零点所在区间为．

故选：．

10．【解答】解：令，可得或，

令，可得，

，可得．

则．

作出图象

结合图象可得或时，恰有两零点．

故选：．

11．【解答】解：函数，，

，，

，，

在同一个直角坐标系中画出，，，的图象，如图：

，可得，，

所以．

故选：．

12．【解答】解：根据函数，

构造函数，，作出函数的大致图象如图所示，

结合函数图象可知，当时，不符合题意，故．

易知直线恒过点，

当直线与曲线相切时，

设切点坐标为，，因为，切线的斜率为，

，，切线的斜率为．

结合图象可知，当时，直线与函数的图象有三个不同的交点，

即函数有三个不同的零点，

故实数的取值范围是．

故选：．

二．解答题（共2小题）

13．【解答】解：（1）根据题意，函数，则有，解可得，

即函数的定义域为，，，

根据奇函数的定义，对于，，，则有，

即，化简得：即；

（2）若函数有零点，则直线与曲线有交点，

又由，那么，则的值域为，，；

故由，，，

解得：，

即的取值范围为：，，．

14．【解答】解：（1）当时，，

由，得，

即，解得或．

不等式的解集为，，；

（2）函数在，上存在零点方程在，上有解，

即方程在，上有解，

即在，上有解，函数在，上是减函数

则，，

从而，实数的取值范围是，．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2020/12/26 20:59:37；用户：郭天军；邮箱：wcdezx37@xyh.com；学号：26222372