

【中考真题】2021年山东省济南市商河县清华园学校中考数学模拟试卷(34)(含答案解析)
展开2021年山东省济南市商河县清华园学校中考数学模拟试卷(34)
一.选择题(共14小题)
1.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有300米.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
2.如图所示,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=﹣和y=的图象交于点A和点B,若点C是x轴上任意一点,连接AC,BC,则△ABC的面积为( )
A.6 B.7 C.8 D.14
3.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上,若AB=1,则k的值为( )
A.1 B. C. D.2
4.在反比例函数y=﹣图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是( )
A.y3<y2<y1 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
5.如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3=的图象在同一平面直角坐标系中,若y3>y1>y2,则自变量x的取值范围是( )
A.x<﹣1 B.﹣0.5<x<0或x>1
C.0<x<1 D.x<﹣1或0<x<1
6.点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于( )
A.5 B.3 C.﹣3 D.﹣1
7.将直线y=﹣2x﹣1向上平移两个单位,平移后的直线所对应的函数关系式为( )
A.y=﹣2x﹣5 B.y=﹣2x﹣3 C.y=﹣2x+1 D.y=﹣2x+3
8.下列关于一次函数y=kx+b(k<0,b>0)的说法,错误的是( )
A.图象经过第一、二、四象限
B.y随x的增大而减小
C.图象与y轴交于点(0,b)
D.当x>﹣时,y>0
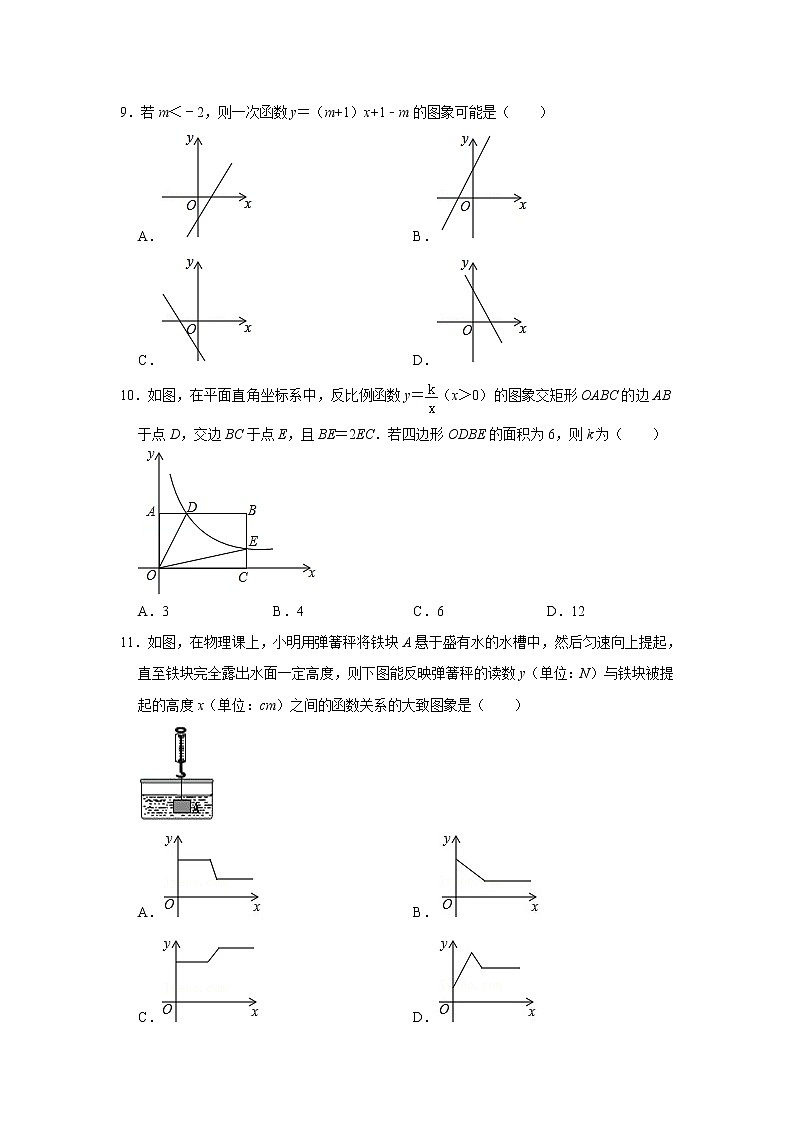
9.若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是( )
A. B.
C. D.
10.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k为( )
A.3 B.4 C.6 D.12
11.如图,在物理课上,小明用弹簧秤将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是( )
A. B.
C. D.
12.已知直线l1:y=﹣3x+b与直线l2:y=﹣kx+m在同一平面直角坐标系中交于点(1,﹣2),那么方程组的解是( )
A. B. C. D.
13.对于反比例函数y=,下列说法中不正确的是( )
A.图象分布在第二、四象限
B.当x>0时,y随x的增大而增大
C.图象经过点(1,﹣2)
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
14.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是( )
A.12 B.24 C.36 D.48
二.填空题(共11小题)
15.现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864m2,那么小道的宽度应是 m.
16.甲、乙两人分别从两地同时出发登山,甲、乙两人距山脚的竖直高度y(米)与登山时间x(分)之间的图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速登山,且速度是甲速度的4倍,那么他们出发 分钟时,乙追上了甲.
17.如图,平行四边形OABC的顶点A在x轴的正半轴上,点D(3,2)在对角线OB上,反比例函数y=(k>0,x>0)的图象经过C、D两点.已知平行四边形OABC的面积是,则点B的坐标为 .
18.如图,在直角坐标系中,以坐标原点O(0,0),A(0,4),B(﹣3,0)为顶点的Rt△AOB,其两个锐角对应的外角角平分线相交于点P,且点P恰好在反比例函数y=的图象上,则k的值为 .
19.已知一次函数y=kx+b的图象经过A(1,﹣1),B(﹣1,3)两点,则k 0(填“>”或“<”)
20.如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 .
21.点(﹣,m)和点(2,n)在直线y=2x+b上,则m与n的大小关系是 .
22.如图,直线y=mx与双曲线y=交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为 .
23.在平面直角坐标系中,将直线y=3x+1先向左平移3个单位长度,接着再向上平移2个单位长度,所得的直线解析式为 .
24.过点(﹣1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线平行.则在线段AB上,横、纵坐标都是整数的点的坐标是 .
25.如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组的解集为 .
三.解答题(共3小题)
26.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,
(1)甲步行的速度为 米/分;
(2)乙走完全程用了 分钟;
(3)求乙到达终点时,甲离终点的距离是多少米?
27.小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)小帅的骑车速度为 千米/小时;点C的坐标为 ;
(2)求线段AB对应的函数表达式;
(3)当小帅到达乙地时,小泽距乙地还有多远?
28.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.
请你根据图象进行探究:
(1)小王和小李的速度分别是多少?
(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.
2021年山东省济南市商河县清华园学校中考数学模拟试卷(34)
参考答案与试题解析
一.选择题(共14小题)
1.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了30分钟;③乙用12分钟追上甲;④乙到达终点时,甲离终点还有300米.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据题意和函数图象中的数据可以判断各个小题中的结论是否正确,从而可以解答本题.
【解答】解:由题意可得:甲步行速度==60(米/分);
故①结论正确;
设乙的速度为:x米/分,
由题意可得:16×60=(16﹣4)x,
解得x=80
∴乙的速度为80米/分;
∴乙走完全程的时间==30(分),
故②结论正确;
由图可得,乙追上甲的时间为:16﹣4=12(分);
故③结论正确;
乙到达终点时,甲离终点距离是:2400﹣(4+30)×60=360(米),
故④结论错误;
故正确的结论有①②③共3个.
故选:C.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
2.如图所示,过y轴正半轴上的任意一点P作x轴的平行线,分别与反比例函数y=﹣和y=的图象交于点A和点B,若点C是x轴上任意一点,连接AC,BC,则△ABC的面积为( )
A.6 B.7 C.8 D.14
【分析】根据两平行直线之间共底三角形的面积相等可知,当C点位于O点时,△ABC的面积与△ABO的面积相等,由此即可求解.
【解答】解:连接OA、OB,如下图所示,
∵AB∥x轴,且△ABC与△ABO共底边AB,
∴△ABC的面积等于△ABO的面积,
则=.
故选:B.
【点评】本题考查了反比例函数的图象和性质,熟练掌握反比例函数上一点向坐标轴作垂线,与坐标轴构成的矩形的面积为|k|这个结论.
3.如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y=(x>0)的图象上,若AB=1,则k的值为( )
A.1 B. C. D.2
【分析】根据题意可以求得OA和AC的长,从而可以求得点C的坐标,进而求得k的值,本题得以解决.
【解答】解:∵等腰直角三角形ABC的顶点A、B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,AB=1,
∴∠BAC=∠BAO=45°,
∴OA=OB=,AC=,
∴点C的坐标为(,),
∵点C在函数y=(x>0)的图象上,
∴k==1,
故选:A.
【点评】本题考查反比例函数图象上点的坐标特征、等腰直角三角形,解答本题的关键是明确题意,利用数形结合的思想解答.
4.在反比例函数y=﹣图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是( )
A.y3<y2<y1 B.y1<y3<y2 C.y2<y3<y1 D.y3<y1<y2
【分析】根据反比例函数图象上点的坐标特征解答.
【解答】解:∵A(x1,y1)在反比例函数y=﹣图象上,x1<0,
∴y1>0,
对于反比例函数y=﹣,在第二象限,y随x的增大而增大,
∵0<x2<x3,
∴y2<y3<0,
∴y2<y3<y1
故选:C.
【点评】本题考查的是反比例函数图象上点的坐标特征,掌握反比例函数的性质、反比例函数的增减性是解题的关键.
5.如图,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3=的图象在同一平面直角坐标系中,若y3>y1>y2,则自变量x的取值范围是( )
A.x<﹣1 B.﹣0.5<x<0或x>1
C.0<x<1 D.x<﹣1或0<x<1
【分析】根据图象,找出双曲线y3落在直线y1上方,且直线y1落在直线y2上方的部分对应的自变量x的取值范围即可.
【解答】解:由图象可知,当x<﹣1或0<x<1时,双曲线y3落在直线y1上方,且直线y1落在直线y2上方,即y3>y1>y2,
所以若y3>y1>y2,则自变量x的取值范围是x<﹣1或0<x<1.
故选:D.
【点评】本题考查了反比例函数与一次函数的交点问题,利用数形结合是解题的关键.
6.点P(a,b)在函数y=3x+2的图象上,则代数式6a﹣2b+1的值等于( )
A.5 B.3 C.﹣3 D.﹣1
【分析】把点P的坐标代入一次函数解析式,得出3a﹣b=﹣2,代入2(3a﹣b)+1即可.
【解答】解:∵点P(a,b)在函数y=3x+2的图象上,
∴b=3a+2,
则3a﹣b=﹣2.
∴6a﹣2b+1=2(3a﹣b)+1=﹣4+1=﹣3
故选:C.
【点评】本题考查了一次函数图象上点的坐标特征,掌握函数图象上点的坐标满足函数关系式.
7.将直线y=﹣2x﹣1向上平移两个单位,平移后的直线所对应的函数关系式为( )
A.y=﹣2x﹣5 B.y=﹣2x﹣3 C.y=﹣2x+1 D.y=﹣2x+3
【分析】根据函数图象向上平移加,向下平移减,可得答案.
【解答】解:直线y=﹣2x﹣1向上平移两个单位,所得的直线是y=﹣2x+1,
故选:C.
【点评】本题考查了一次函数图象与几何变换,图象平移的规律是:上加下减,左加右减.
8.下列关于一次函数y=kx+b(k<0,b>0)的说法,错误的是( )
A.图象经过第一、二、四象限
B.y随x的增大而减小
C.图象与y轴交于点(0,b)
D.当x>﹣时,y>0
【分析】由k<0,b>0可知图象经过第一、二、四象限;由k<0,可得y随x的增大而减小;图象与y轴的交点为(0,b);当x>﹣时,y<0;
【解答】解:∵y=kx+b(k<0,b>0),
∴图象经过第一、二、四象限,
A正确;
∵k<0,
∴y随x的增大而减小,
B正确;
令x=0时,y=b,
∴图象与y轴的交点为(0,b),
∴C正确;
令y=0时,x=﹣,
当x>﹣时,y<0;
D不正确;
故选:D.
【点评】本题考查一次函数的图象及性质;熟练掌握一次函数解析式y=kx+b中,k与b对函数图象的影响是解题的关键.
9.若m<﹣2,则一次函数y=(m+1)x+1﹣m的图象可能是( )
A. B.
C. D.
【分析】由m<﹣2得出m+1<0,1﹣m>0,进而利用一次函数的性质解答即可.
【解答】解:∵m<﹣2,
∴m+1<0,1﹣m>0,
所以一次函数y=(m+1)x+1﹣m的图象经过一,二,四象限,
故选:D.
【点评】本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.
10.如图,在平面直角坐标系中,反比例函数y=(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k为( )
A.3 B.4 C.6 D.12
【分析】连接OB,由矩形的性质和已知条件得出△OBD的面积=△OBE的面积=四边形ODBE的面积=3,在求出△OCE的面积,即可得出k的值.
【解答】解:连接OB,如图所示:
∵四边形OABC是矩形,
∴∠OAD=∠OCE=∠DBE=90°,△OAB的面积=△OBC的面积,
∵D、E在反比例函数y=(x>0)的图象上,
∴△OAD的面积=△OCE的面积,
∴△OBD的面积=△OBE的面积=四边形ODBE的面积=3,
∵BE=2EC,
∴△OCE的面积=△OBE的面积=,
∴k=3;
故选:A.
【点评】本题考查了矩形的性质、三角形面积的计算、反比例函数的图象与解析式的求法;熟练掌握矩形的性质和反比例函数解析式的求法是解决问题的关键.
11.如图,在物理课上,小明用弹簧秤将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧秤的读数y(单位:N)与铁块被提起的高度x(单位:cm)之间的函数关系的大致图象是( )
A. B.
C. D.
【分析】根据在铁块开始露出水面到完全露出水面时,排开水的体积逐渐变小,根据阿基米德原理和称重法可知y的变化,注意铁块露出水面前读数y不变,离开水面后y不变,即可得出答案.
【解答】解:露出水面前排开水的体积不变,受到的浮力不变,根据称重法可知y不变;
铁块开始露出水面到完全露出水面时,排开水的体积逐渐变小,根据阿基米德原理可知受到的浮力变小,根据称重法可知y变大;
铁块完全露出水面后一定高度,不再受浮力的作用,弹簧秤的读数为铁块的重力,故y不变.
故选:C.
【点评】本题考查了函数的图象,用到的知识点是函数值随高度的变化,注意分析y随x的变化而变化的趋势,而不一定要通过求解析式来解决.
12.已知直线l1:y=﹣3x+b与直线l2:y=﹣kx+m在同一平面直角坐标系中交于点(1,﹣2),那么方程组的解是( )
A. B. C. D.
【分析】根据两个一次函数组成的方程组的解就是两函数图象的交点可得答案.
【解答】解:∵直线l1:y=﹣3x+b与直线l2:y=﹣kx+m在同一坐标系中的图象交于点(1,﹣2),
∴方程组的解是,
故选:A.
【点评】此题主要考查了一次函数与二元一次方程组的关系,关键是掌握凡是函数图象经过的点必能满足解析式.
13.对于反比例函数y=,下列说法中不正确的是( )
A.图象分布在第二、四象限
B.当x>0时,y随x的增大而增大
C.图象经过点(1,﹣2)
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
【分析】由反比例函数的性质可求解.
【解答】解:∵反比例函数y=,
∴图象分布在第二、第四象限,当x>0时,y随x的增大而增大,当x=1时,y=﹣2,
∴选项A,B,C正确
∵反比例函数y=图象在每个象限内y随x的增大而增大,
∴选项D错误
故选:D.
【点评】本题考查了反比例函数的性质,熟练运用反比例函数的性质是本题的关键.
14.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是( )
A.12 B.24 C.36 D.48
【分析】由图2知,AB=BC=10,当BP⊥AC时,y的值最小,即△ABC中,AC边上的高为8(即此时BP=8),即可求解.
【解答】解:由图2知,AB=BC=10,
当BP⊥AC时,y的值最小,即△ABC中,AC边上的高为8(即此时BP=8),
当y=8时,PC===6,
△ABC的面积=×AC×BP=8×12=48,
故选:D.
【点评】本题是运动型综合题,考查了动点问题的函数图象、解直角三角形、图形面积等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.
二.填空题(共11小题)
15.现要在一个长为40m,宽为26m的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为864m2,那么小道的宽度应是 2 m.
【分析】设小道进出口的宽度为x米,然后利用其种植花草的面积为864m2列出方程求解即可.
【解答】解:设小道进出口的宽度为x米,依题意得(40﹣2x)(26﹣x)=864,
整理,得x2﹣46x+88=0.
解得,x1=2,x2=44.
∵44>40(不合题意,舍去),
∴x=2.
答:小道进出口的宽度应为2米.
故答案为:2.
【点评】本题考查了一元二次方程的应用,解题的关键是根据种植花草的面积为864m2找到正确的等量关系并列出方程.
16.甲、乙两人分别从两地同时出发登山,甲、乙两人距山脚的竖直高度y(米)与登山时间x(分)之间的图象如图所示,若甲的速度一直保持不变,乙出发2分钟后加速登山,且速度是甲速度的4倍,那么他们出发 分钟时,乙追上了甲.
【分析】求出直线CD、AB的解析式,利用方程组确定交点坐标即可.
【解答】解:如图,∵C(0,50),D(10,150),
∴直线CD的解析式为y=10x+50,
由题意A(2,30),
甲的速度为10米/分,
∴乙加速后的速度为40米/分,
∴乙从A到B的时间==3,
∴B(5,150),
∴直线AB的解析式为y=40x﹣50,
由,解得,
∴那么他们出发分钟时,乙追上了甲.
故答案为.
【点评】本题考查了行程问题的数量关系的运用,待定系数法求一次函数的解析式的运用,一次函数与一元一次方程的运用,解答时求出一次函数的解析式是关键.
17.如图,平行四边形OABC的顶点A在x轴的正半轴上,点D(3,2)在对角线OB上,反比例函数y=(k>0,x>0)的图象经过C、D两点.已知平行四边形OABC的面积是,则点B的坐标为 (,3) .
【分析】分别过点D、B作DE⊥x轴于点E,BF⊥x轴于点F,延长BC交y轴于点H,易求得CH=AF,求出反比例函数y=,设点C坐标为(a,),通过证得△ODE∽△OBF,得到OF=,即可求得OA=OF﹣AF=OF﹣HC=﹣a,得到点B坐标为(,),然后根据平行四边形的面积公式得到关于a的方程,解方程可得出结果.
【解答】解:如图,分别过点D、B作DE⊥x轴于点E,BF⊥x轴于点F,延长BC交y轴于点H,
∵四边形OABC是平行四边形,
∴OA=BC,
∵BH=OF,
∴CH=AF,
∵点D(3,2)在对角线OB上,反比例函数(k>0,x>0)的图象经过C、D两点,
∴k=2×3=6,即反比例函数解析式为y=,
∴设点C坐标为(a,),
∵DE∥BF,
∴△ODE∽△OBF,
∴,
∴,
∴OF=,
∴OA=OF﹣AF=OF﹣HC=﹣a,
∴点B坐标为(,),
∵平行四边形OABC的面积是,
∴,
解得a1=2,a2=﹣2(舍去),
∴点B坐标为(,3),
故答案为(,3).
【点评】本题考查了反比例函数图象上点的坐标特征、待定系数法求反比例函数解析式、平行四边形的性质、熟练掌握平行四边形的性质是解题的关键.
18.如图,在直角坐标系中,以坐标原点O(0,0),A(0,4),B(﹣3,0)为顶点的Rt△AOB,其两个锐角对应的外角角平分线相交于点P,且点P恰好在反比例函数y=的图象上,则k的值为 ﹣36 .
【分析】过P分别作AB、x轴、y轴的垂线,垂足分别为C、D、E,如图,利用勾股定理计算出AB=5,根据角平分线的性质得PE=PC=PD,设P(﹣t,t),利用面积的和差得到×t×(t﹣4)+×5×t+×t×(t﹣3)+×3×4=t×t,求出t得到P点坐标,然后把P点坐标代入y=中求出k的值.
【解答】解:过P分别作AB、x轴、y轴的垂线,垂足分别为C、D、E,如图,
∵A(0,4),B(﹣3,0),
∴OA=4,OB=3,
∴AB==5,
∵△OAB的两个锐角对应的外角角平分线相交于点P,
∴PE=PC,PD=PC,
∴PE=PC=PD,
设P(﹣t,t),则PC=t,
∵S△PAE+S△PAB+S△PBD+S△OAB=S矩形PEOD,
∴×t×(t﹣4)+×5×t+×t×(t﹣3)+×3×4=t×t,
解得t=6,
∴P(﹣6,6),
把P(﹣6,6)代入y=得k=﹣6×6=﹣36.
故答案为﹣36.
【点评】本题考查反比例函数图象上点的坐标特征:反比例函数图象上点的坐标满足其解析式.也考查了角平分线的性质和三角形面积公式.
19.已知一次函数y=kx+b的图象经过A(1,﹣1),B(﹣1,3)两点,则k < 0(填“>”或“<”)
【分析】根据A(1,﹣1),B(﹣1,3),利用横坐标和纵坐标的增减性判断出k的符号.
【解答】解:∵A点横坐标为1,B点横坐标为﹣1,
根据﹣1<1,3>﹣1,
可知,随着横坐标的增大,纵坐标减小了,
∴k<0.
故答案为<.
【点评】本题考查了一次函数图象上点的坐标特征,根据点的坐标判断出函数的增减性是解题的关键.
20.如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 x≥1 .
【分析】先利用解析式y=x+2确定P点坐标,然后结合图象,写出直线y=ax+c在直线y=x+2的下方所对应的自变量的范围即可.
【解答】解:把P(m,3)代入y=x+2得m+2=3,解得m=1,
∴P(1,3),
∵x≥1时,x+2≥ax+c,
∴关于x的不等式x+2≥ax+c的不等式的解为x≥1.
故答案为x≥1.
【点评】本题考查了一次函数与一元一次不等式:认真体会一次函数与一元一次不等式(组)之间的内在联系及数形结合思想.理解一次函数的增减性是解决本题的关键.
21.点(﹣,m)和点(2,n)在直线y=2x+b上,则m与n的大小关系是 m<n .
【分析】先根据直线的解析式判断出函数的增减性,再根据一次函数的性质即可得出结论.
【解答】解:∵直线y=2x+b中,k=2>0,
∴此函数y随着x的增大而增大,
∵﹣<2,
∴m<n.
故答案为m<n.
【点评】本题考查的是一次函数图象上点的坐标特点,熟知一次函数的增减性是解答此题的关键.
22.如图,直线y=mx与双曲线y=交于A,B两点,过点A作AM⊥x轴,垂足为点M,连接BM,若S△ABM=2,则k的值为 ﹣2 .
【分析】根据反比例的图象关于原点中心对称得到点A与点B关于原点中心对称,则S△OAM=S△OBM,而S△ABM=2,S△OAM=1,然后根据反比例函数y=(k≠0)系数k的几何意义即可得到k=﹣2.
【解答】解:∵直线y=mx与双曲线y=交于A,B两点,
∴点A与点B关于原点中心对称,
∴S△OAM=S△OBM,
而S△ABM=2,
∴S△OAM=1,
∴|k|=1,
∵反比例函数图象在第二、四象限,
∴k<0,
∴k=﹣2.
故答案为:﹣2.
【点评】本题考查了反比例函数与一次函数的交点问题,熟知从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|是解答此题的关键.
23.在平面直角坐标系中,将直线y=3x+1先向左平移3个单位长度,接着再向上平移2个单位长度,所得的直线解析式为 y=3x+12 .
【分析】根据“左加右减,上加下减”的规律写出函数解析式即可.
【解答】解:将直线y=3x+1先向左平移3个单位长度,接着再向上平移2个单位长度得到直线y=3(x+3)+1+2,即y=3x+12,
故答案为y=3x+12.
【点评】本题考查了一次函数图象与几何变换,掌握“左加右减,上加下减”直线平移的规律,属于基础题,中考常考题型
24.过点(﹣1,7)的一条直线与x轴,y轴分别相交于点A,B,且与直线平行.则在线段AB上,横、纵坐标都是整数的点的坐标是 (1,4),(3,1) .
【分析】依据与直线平行设出直线AB的解析式y=﹣x+b;代入点(﹣1,7)即可求得b,然后求出与x轴的交点横坐标,列举才符合条件的x的取值,依次代入即可.
【解答】解:∵过点(﹣1,7)的一条直线与直线平行,设直线AB为y=﹣x+b;
把(﹣1,7)代入y=﹣x+b;得7=+b,
解得:b=,
∴直线AB的解析式为y=﹣x+,
令y=0,得:0=﹣x+,
解得:x=,
∴0<x<的整数为:1、2、3;
把x等于1、2、3分别代入解析式得4、、1;
∴在线段AB上,横、纵坐标都是整数的点的坐标是(1,4),(3,1).
故答案为:(1,4),(3,1).
【点评】本题考查了待定系数法求解析式以及直线上点的情况,列举出符合条件的x的值是本题的关键.
25.如图,一次函数y=﹣x﹣2与y=2x+m的图象相交于点P(n,﹣4),则关于x的不等式组的解集为 ﹣2<x<2 .
【分析】先将点P(n,﹣4)代入y=﹣x﹣2,求出n的值,再找出直线y=2x+m落在y=﹣x﹣2的下方且都在x轴下方的部分对应的自变量的取值范围即可.
【解答】解:∵一次函数y=﹣x﹣2的图象过点P(n,﹣4),
∴﹣4=﹣n﹣2,解得n=2,
∴P(2,﹣4),
又∵y=﹣x﹣2与x轴的交点是(﹣2,0),
∴关于x的不等式组的解集为:﹣2<x<2.
故答案为:﹣2<x<2.
【点评】本题考查了一次函数与一元一次不等式,体现了数形结合的思想方法,准确确定出n的值,是解答本题的关键.
三.解答题(共3小题)
26.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,
(1)甲步行的速度为 60 米/分;
(2)乙走完全程用了 30 分钟;
(3)求乙到达终点时,甲离终点的距离是多少米?
【分析】(1)根据函数图象中的数据,可以计算出甲步行的速度;
(2)根据(1)中的结果和图象中的数据,可以计算出乙步行的速度,然后即可得到乙走完全程用的时间;
(3)根据图象中的数据和题意,可以计算出乙到达终点时,甲离终点的距离是多少米.
【解答】解:(1)由图可得,
甲步行的速度为:240÷4=60(米/分),
故答案为:60;
(2)乙的速度为:60+240÷(16﹣4)=80(米/分),
即乙走完全程的时间:2400÷80=30(分钟),
故答案为:30;
(3)2400﹣(30+4)×60
=2400﹣34×60
=2400﹣2040
=360(米),
答:乙到达终点时,甲离终点的距离是360米.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
27.小泽和小帅两同学分别从甲地出发,骑自行车沿同一条路到乙地参加社会实践活动.如图折线OAB和线段CD分别表示小泽和小帅离甲地的距离y(单位:千米)与时间x(单位:小时)之间函数关系的图象.根据图中提供的信息,解答下列问题:
(1)小帅的骑车速度为 16 千米/小时;点C的坐标为 (0.5,0) ;
(2)求线段AB对应的函数表达式;
(3)当小帅到达乙地时,小泽距乙地还有多远?
【分析】(1)根据函数图象中的数据可以求得小帅的骑车速度和点C的坐标;
(2)根据函数图象中的数据可以求得线段AB对应的函数表达式;
(3)将x=2代入(2)中的函数解析式求出相应的y的值,再用24减去此时的y值即可求得当小帅到达乙地时,小泽距乙地的距离.
【解答】解:(1)由图可得,
小帅的骑车速度是:(24﹣8)÷(2﹣1)=16千米/小时,
点C的横坐标为:1﹣8÷16=0.5,
∴点C的坐标为(0.5,0),
故答案为:16千米/小时,(0.5,0);
(2)设线段AB对应的函数表达式为y=kx+b(k≠0),
∵A(0.5,8),B(2.5,24),
∴,
解得:,
∴线段AB对应的函数表达式为y=8x+4(0.5≤x≤2.5);
(3)当x=2时,y=8×2+4=20,
∴此时小泽距离乙地的距离为:24﹣20=4(千米),
答:当小帅到达乙地时,小泽距乙地还有4千米.
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.
28.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.
请你根据图象进行探究:
(1)小王和小李的速度分别是多少?
(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.
【分析】(1)根据题意和函数图象中的数据可以分别求得王和小李的速度;
(2)根据(1)中的结果和图象中的数据可以求得点C的坐标,从而可以解答本题.
【解答】解:(1)由图可得,
小王的速度为:30÷3=10km/h,
小李的速度为:(30﹣10×1)÷1=20km/h,
答:小王和小李的速度分别是10km/h、20km/h;
(2)小李从乙地到甲地用的时间为:30÷20=1.5h,
当小李到达甲地时,两人之间的距离为:10×1.5=15km,
∴点C的坐标为(1.5,15),
设线段BC所表示的y与x之间的函数解析式为y=kx+b,
,得,
即线段BC所表示的y与x之间的函数解析式是y=30x﹣30(1≤x≤1.5).
【点评】本题考查一次函数的应用,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/11/14 23:16:50;用户:张家港二中;邮箱:zjg2z@xyh.com;学号:41479226
菁优网APP 菁优网公众号 菁优网小程序
【中考真题】2021年山东省济南市商河县清华园学校中考数学模拟试卷(26)(含答案解析): 这是一份【中考真题】2021年山东省济南市商河县清华园学校中考数学模拟试卷(26)(含答案解析),共30页。试卷主要包含了﹣7的相反数为,2020年新冠肺炎席卷全球,计算的结果是,函数y=kx+k与y=等内容,欢迎下载使用。
【中考真题】2021年山东省济南市商河县清华园学校中考数学模拟试卷(22)(含答案解析): 这是一份【中考真题】2021年山东省济南市商河县清华园学校中考数学模拟试卷(22)(含答案解析),共22页。试卷主要包含了现有以下命题,给出下列5个命题,下列命题中,正确的是等内容,欢迎下载使用。
【中考真题】2021年山东省济南市商河县清华园学校中考数学模拟试卷(28)(含答案解析): 这是一份【中考真题】2021年山东省济南市商河县清华园学校中考数学模拟试卷(28)(含答案解析),共32页。试卷主要包含了实数﹣的绝对值是,如图所示几何体的左视图正确的是,下列计算正确的是,如图,正方形ABCD的顶点A等内容,欢迎下载使用。












