





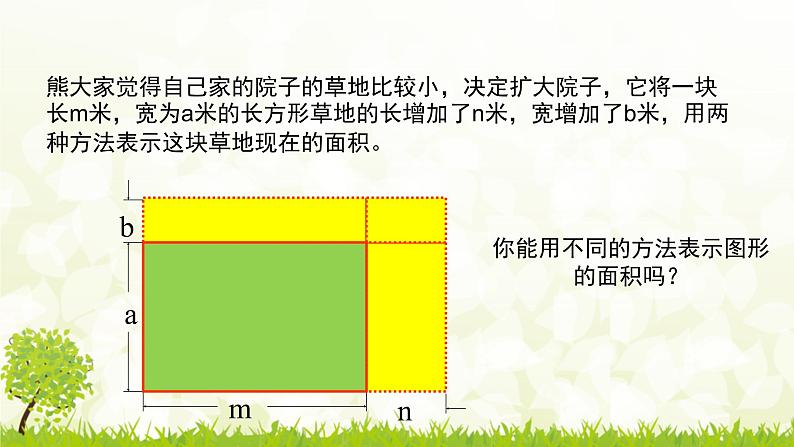
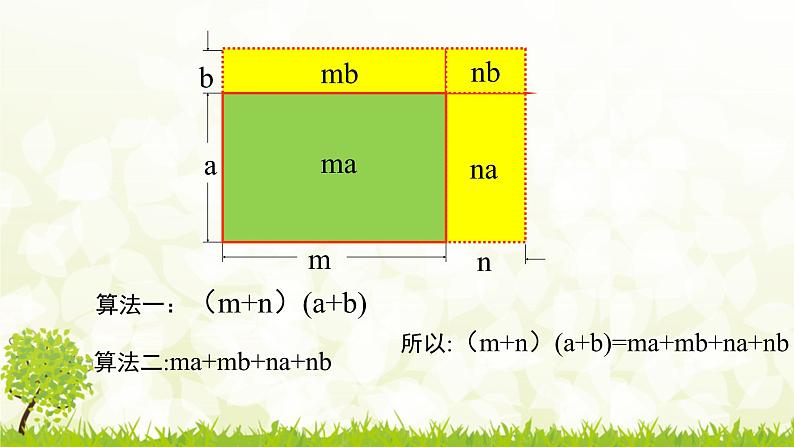



所属成套资源:北师大七年级下册数学同步备课课件PPT+练习
北师大版七年级下册4 整式的乘法公开课ppt课件
展开
这是一份北师大版七年级下册4 整式的乘法公开课ppt课件,文件包含北师大版七年级数学下册143多项式乘多项式pptx、北师大版七年级数学下册143多项式乘多项式docx等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
1.4.3 多项式乘多项式一.选择题(共10小题)1.若2x+m与x+3的乘积中不含x的一次项,则m的值为( )A.﹣6 B.0 C.﹣2 D.32.根据图中数据,计算大长方形的面积,通过不同的计算方法,你发现的结论是( )A.(a+b)(a+2b)=a2+3ab+2b2 B.(3a+b)(a+b)=3a2+4ab+b2 C.(2a+b)(a+b)=2a2+3ab+b2 D.(3a+2b)(a+b)=3a2+5ab+2b23.若(x+3)(x﹣5)=x2+mx﹣n,则( )A.m=﹣2 n=15 B.m=2 n=﹣15 C.m=﹣2 n=﹣15 D.m=2 n=154.如果(x﹣4)(x+8)=x2+mx+n,那么m+n的值为( )A.36 B.﹣28 C.28 D.﹣365.若(x+m)(x﹣5)=x2+nx﹣10,则mn﹣m+n的值是( )A.﹣11 B.﹣7 C.﹣6 D.﹣56.如果(x+1)(x2﹣5ax+a)的乘积中不含x2项,则a为( )A. B.﹣ C.﹣5 D.57.若(x+2)(x﹣3)=x2+ax+b,则a,b的值分别为( )A.﹣1,﹣6 B.﹣5,﹣6 C.﹣5,6 D.﹣1,68.若(x2﹣px+q)(x﹣3)展开后不含x的一次项,则p与q的关系是( )A.p=3q B.p+3q=0 C.q+3p=0 D.q=3p9.在下列多项式中,与﹣x﹣y相乘的结果为x2﹣y2的多项式是( )A.x﹣y B.x+y C.﹣x+y D.﹣x﹣y10.小淇用大小不同的9个长方形拼成一个大的长方形ABCD,则图中阴影部分的面积是( )A.(a+1)(b+3) B.(a+3)(b+1) C.(a+1)(b+4) D.(a+4)(b+1)二.填空题(共5小题)11.若计算(x+m)(4x﹣3)﹣5x所得的结果中不含x的一次项,则常数m的值为 .12.若x+y=3,且xy=1,则代数式(5﹣x)(5﹣y)= .13.若(x﹣1)(x2+5ax﹣a)的乘积中不含x2项,则a的值为 .14.若(x+3)(x+m)=x2﹣2x﹣15.则m= .15.如图,现有A类、B类正方形卡片和C类长方形卡片各若干张,若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要 张C类卡片.三.解答题(共3小题)16.已知x2﹣x+1=0,求代数式(x+1)2﹣(x+1)(2x﹣1)的值.17.阅读:若x满足(60﹣x)(x﹣40)=30,求(60﹣x)2+(x﹣40)2的值.解:设(60﹣x)=a,(x﹣40)=b,则(60﹣x)(x﹣40)=ab= ,a+b=(60﹣x)+(x﹣40)= ,所以(60﹣x)2+(x﹣40)2=a2+b2=(a+b)2﹣2ab= .请仿照上例解决下面的问题:(1)补全题目中横线处;(2)已知(30﹣x)(x﹣20)=﹣10,求(30﹣x)2+(x﹣20)2的值; (3)若x满足(2023﹣x)2+(2022﹣x)2=2021,求(2023﹣x)(x﹣2022)的值; (4)如图,正方形ABCD的边长为x,AE=10,CG=25,长方形EFGD的面积是400,四边形NGDH和MEDQ都是正方形,PQDH是长方形,求图中阴影部分的面积(结果必须是一个具体数值).18.化简:(1)(2x)3(﹣5xy2); (2)(3x+2)(x+2).
多项式乘多项式参考答案与试题解析一.选择题(共10小题)1.【分析】首先根据多项式乘多项式的方法,求出2x+m与x+3的乘积;然后根据2x+m与x+3的乘积中不含x的一次项,可得:x的一次项的系数等于0,据此求出m的值为多少即可.【解答】解:(2x+m)(x+3)=2x2+(m+6)x+3m,∵2x+m与x+3的乘积中不含x的一次项,∴m+6=0,解得:m=﹣6.故选:A.【点评】此题主要考查了多项式乘多项式的方法,要熟练掌握,解答此题的关键是要明确:(1)相乘时,按一定的顺序进行,必须做到不重不漏;(2)多项式与多项式相乘,仍得多项式,在合并同类项之前,积的项数应等于原多项式的项数之积.2.【分析】大长方形的长为3a+2b,宽为a+b,表示出面积;也可以由三个边长为a的正方形,2个边长为b的正方形,以及5个长为b,宽为a的长方形面积之和表示,即可得到正确的选项.【解答】解:根据图形得:(3a+2b)(a+b)=3a2+5ab+2b2.故选:D.【点评】此题考查了多项式乘多项式,弄清题意是解本题的关键.3.【分析】根据多项式乘多项式运算法则,由(x+3)(x﹣5)=x2+mx﹣n得x2﹣2x﹣15=x2+mx﹣n,故m=﹣2,n=15.那么,A符合题意.【解答】解:∵(x+3)(x﹣5)=x2+mx﹣n,∴x2﹣5x+3x﹣15=x2+mx﹣n.∴x2﹣2x﹣15=x2+mx﹣n.∴m=﹣2,b=15.故选:A.【点评】本题主要考查整式运算中的多项式乘多项式,熟练掌握多项式乘以多项式的运算法则是解题关键.4.【分析】先将(x﹣4)(x+8)展开,然后与x2+mx+n找准对应的系数,即可得到m、n的值.【解答】解:∵(x﹣4)(x+8)=x2+4x﹣32,(x﹣4)(x+8)=x2+mx+n,∴m=4,n=﹣32,∴m+n的值为﹣28,故选:B.【点评】本题考查多项式乘以多项式,解题的关键是明确多项式乘以多项式的方法,找准对应的系数.5.【分析】先根据多项式乘多项式法则展开,再合并同类项,最后求出答案即可.【解答】解:(x+m)(x﹣5)=x2﹣5x+mx﹣5m=x2+(m﹣5)x﹣5m,∵(x+m)(x﹣5)=x2+nx﹣10,∴m﹣5=n,5m=10,∴m=2,n=﹣3,∴mn﹣m+n=2×(﹣3)﹣2+(﹣3)=﹣6﹣2﹣3=﹣11.故选:A.【点评】本题考查了多项式乘多项式法则,能正确根据多项式乘多项式的运算法则进行计算是解此题的关键.6.【分析】先根据多项式乘以多项式的法则展开,再合并同类项,根据已知得出方程﹣5a+1=0,求出即可.【解答】解:(x+1)(x2﹣5ax+a)=x3﹣5ax2+ax+x2﹣5ax+a=x3+(﹣5a+1)x2+ax+a,∵(x+1)(x2﹣5ax+a)的乘积中不含x2项,∴﹣5a+1=0,a=,故选:A.【点评】本题考查了多项式乘以多项式的法则,关键是能根据题意得出关于a的方程.7.【分析】已知等式左边利用多项式乘以多项式法则计算,利用多项式相等的条件即可求出a与b的值.【解答】解:∵(x+2)(x﹣3)=x2﹣x﹣6=x2+ax+b,∴a=﹣1,b=﹣6.故选:A.【点评】此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.8.【分析】利用多项式乘多项式法则计算,令一次项系数为0求出p与q的关系式即可.【解答】解:(x2﹣px+q)(x﹣3)=x3﹣3x2﹣px2+3px+qx﹣3q=x3+(﹣p﹣3)x2+(3p+q)x﹣3q,∵结果不含x的一次项,∴q+3p=0.故选:C.【点评】此题考查了多项式乘多项式,熟练掌握法则是解本题的关键.9.【分析】依据多项式乘多项式法则进行判断即可.【解答】解:(x﹣y)(﹣x﹣y)=y2﹣x2,故A错误;(﹣x﹣y)(x+y)=﹣x2﹣2xy﹣y2,故B错误;(﹣x+y)(﹣x﹣y)=x2﹣y2,故C正确;(﹣x﹣y)(﹣x﹣y)=x2+2xy+y2,故D错误.故选:C.【点评】本题主要考查的是多项式乘多项式,熟练掌握多项式乘多项式法则是解题的关键.10.【分析】根据平移和长方形面积公式即可求解.【解答】解:由平移可知,图中阴影部分的长为(a+3),宽为(b+1),则图中阴影部分的面积是(a+3)(b+1).故选:B.【点评】考查了多项式乘多项式,关键是根据平移得到图中阴影部分的长和宽.二.填空题(共5小题)11.【分析】直接利用多项式乘法结合一次项次数为零进而得出答案.【解答】解:(x+m)(4x﹣3)﹣5x=4x2﹣3x+4mx﹣3m﹣5x=4x2+(4m﹣8)x﹣3m,∵(x+m)(4x﹣3)﹣5x所得的结果中不含x的一次项,∴4m﹣8=0,解得:m=2.故答案为:2.【点评】此题主要考查了多项式乘多项式,正确掌握相关运算法则是解题关键.12.【分析】利用多项式乘多项式法则,先计算(5﹣x)(5﹣y),再代入求值.【解答】解:(5﹣x)(5﹣y)=25﹣5y﹣5x+xy=25﹣5(x+y)+xy∵x+y=3,xy=1,∴原式=25﹣5×3+1=11.故答案为:11.【点评】本题考查了多项式乘多项式,掌握多项式乘多项式法则是解决本题的关键.13.【分析】先根据多项式的乘法法则展开,再根据题意,二次项的系数等于0列式求解即可.【解答】解:原式=x3+5ax2﹣ax﹣x2﹣5ax+a=x3+(5a﹣1)x2﹣6ax+a,∵乘积中不含x2项,∴5a﹣1=0,解得:a=0.2.故答案为:0.2.【点评】本题主要考查多项式与多项式的乘法,运算法则需要熟练掌握,不含某一项就让这一项的系数等于0是解题的关键.14.【分析】已知等式左边利用多项式乘多项式法则计算,利用多项式相等的条件求出m的值即可.【解答】解:已知等式整理得:x2+(m+3)x+3m=x2﹣2x﹣15,∴3m=﹣15,即m=﹣5,则m的值是﹣5,故答案为:﹣5.【点评】此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.15.【分析】用长乘以宽,列出算式,根据多项式乘以多项式的运算法则展开,然后根据A、B、C类卡片的形状可得答案.【解答】解:∵(3a+b)(a+2b)=3a2+6ab+ab+2b2=3a2+7ab+2b2,∴若要拼一个长为(3a+b),宽为(a+2b)的大长方形,则需要A类3张,B类2张,C类7张.故答案为:7.【点评】本题考查了多项式乘以多项式在几何图形问题中的应用,数形结合并明确多项式乘以多项式的运算法则是解题的关键.三.解答题(共3小题)16.【分析】根据多项式乘多项式进行化简,然后整体代入即可求值.【解答】解:原式=x2+2x+1﹣2x2+x﹣2x+1=﹣x2+x+2,当x2﹣x+1=0,即﹣x2+x=1时,原式=1+2=3.【点评】本题考查了多项式乘多项式,解决本题的关键是掌握多项式乘多项式.17.【分析】(1)直接代入计算,并根据完全平方公式可解决问题即可;(2)模仿例题,利用换元法解决问题即可;(3)设2023﹣x=m,2022﹣x=n,则m2+n2=2021,m﹣n=1,根据(m﹣n)2可得mn的值,从而得结论;(4)表示DE和DG的长,根据长方形EFGD的面积是400列等式,可得a﹣b=15,ab=400,从而得结论.【解答】解:(1)设(60﹣x)=a,(x﹣40)=b,则(60﹣x)(x﹣40)=ab=30,a+b=(60﹣x)+(x﹣40)=20,所以(60﹣x)2+(x﹣40)2=a2+b2=(a+b)2﹣2ab=400﹣60=340;故答案为:30,20,340;(2)设30﹣x=a,x﹣20=b,则ab=﹣10,a+b=10,∴(30﹣x)2+(x﹣20)2=a2+b2=(a+b)2﹣2ab=102﹣2×(﹣10)=120;(3)设2023﹣x=m,2022﹣x=n,则m2+n2=2021,m﹣n=1,∵(m﹣n)2=m2﹣2mn+n2,∴1=2021﹣2mn,∴mn=1010,即(2023﹣x)(x﹣2022)=﹣1010;(4)由题意得:DE=x﹣10,DG=x﹣25,则(x﹣10)(x﹣25)=400,设a=x﹣10,b=x﹣25,则a﹣b=15,ab=400,∴S阴=(a+b)2=(a﹣b)2+4ab=152+4×400=1825.【点评】本题考查完全平方公式,换元法等知识,解题的关键是学会利用换元法解决问题,熟练掌握完全平方公式.18.【分析】(1)先算积的乘方,然后再利用单项式乘以单项式计算法则进行计算即可;(2)根据多项式乘以多项式的计算法则进行计算即可.【解答】解:(1)原式=8x3•(﹣5xy2)=﹣8x3•5xy2=﹣40x4y2;(2)原式=3x2+6x+2x+4=3x2+8x+4.【点评】本题考查了整式的混合运算,掌握运算法则是解题的关键.
相关课件
这是一份北师大版七年级下册4 整式的乘法课堂教学课件ppt,共19页。PPT课件主要包含了a+bm+n,+an,+bm,+bn,-06•x,x•x,两项相乘时先定符号,-2x•y,+y•x,y•y等内容,欢迎下载使用。
这是一份初中数学北师大版七年级下册4 整式的乘法示范课ppt课件,文件包含143整式的乘法pptx、14整式的乘法第3课时多项式与多项式相乘doc等2份课件配套教学资源,其中PPT共23页, 欢迎下载使用。
这是一份数学七年级下册第一章 整式的乘除4 整式的乘法优秀ppt课件,共24页。PPT课件主要包含了学习目标,导入新课,讲授新课,n+b,a+bm+n,+an,+bm,+bn,多项式的乘法,单项式×多项式等内容,欢迎下载使用。










