




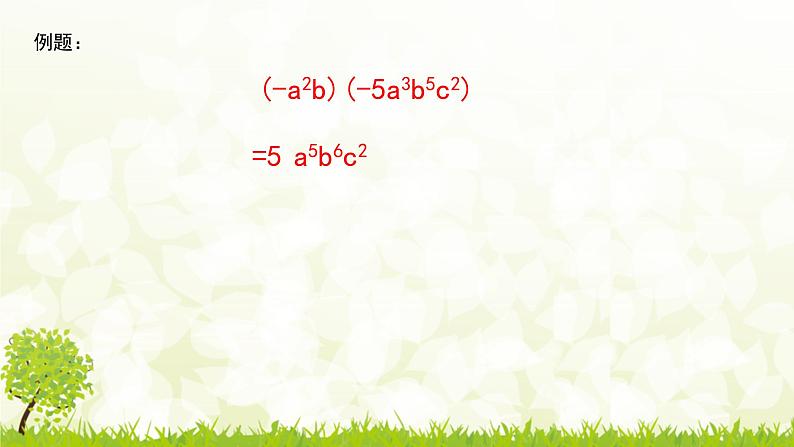




所属成套资源:北师大七年级下册数学同步备课课件PPT+练习
初中数学北师大版七年级下册4 整式的乘法试讲课课件ppt
展开
这是一份初中数学北师大版七年级下册4 整式的乘法试讲课课件ppt,文件包含北师大版七年级数学下册142单项式乘多项式课件pptx、北师大版七年级数学下册142单项式乘多项式docx等2份课件配套教学资源,其中PPT共19页, 欢迎下载使用。
1.4.2 单项式乘多项式一.选择题(共10小题)1.计算:a2(a﹣2b)=( )A.a3﹣a2b B.a3﹣2a2b C.a3﹣2ab2 D.a3﹣a2b22.下列运算正确的是( )A.b5÷b3=b2 B.(b5)3=b8 C.b3b4=b12 D.a(a﹣2b)=a2+2ab3.若要使x(x2+a)+3x﹣2b=x3+5x+4恒成立,则a,b的值分别是( )A.﹣2,﹣2 B.2,2 C.2,﹣2 D.﹣2,24.已知a﹣b=3,b﹣c=﹣2,则代数式a2﹣ac﹣b(a﹣c)的值为( )A.4 B.﹣4 C.3 D.﹣35.若a2﹣2a﹣3=0,代数式×的值是( )A.0 B.﹣ C.2 D.﹣6.计算(﹣3x)•(5x﹣1)的结果是( )A.﹣15x2﹣3x B.﹣15x2+3x C.﹣15x2﹣1 D.﹣15x2+17.若x﹣y+3=0,则x(x﹣4y)+y(2x+y)的值为( )A.9 B.﹣9 C.3 D.﹣38.已知实数m,n,p,q满足m+n=p+q=4,mp+nq=4,则(m2+n2)pq+mn(p2+q2)=( )A.48 B.36 C.96 D.无法计算9.如果(amb•abn)5=a10b15,那么3m(n2+1)的值是( )A.8 B.10 C.12 D.1510.已知A=2x,B是多项式,在计算B+A时,小马虎同学把B+A看成了B÷A,结果得x2+x,则B+A=( )A.2x3+x2+2x B.2x3﹣x2+2x C.2x3+x2﹣2x D.2x3﹣x2﹣2x二.填空题(共5小题)11.将x﹣1(x﹣y)﹣2z表示成只含有正整数的指数幂形式:x﹣1(x﹣y)﹣2z= .12.计算:3a•(2a﹣5)= .13.已知3ab•A=6a2b﹣9ab2,则A= .14.通过计算几何图形的面积可以得到一些恒等式,根据如图的长方形面积写出的恒等式为 .15.计算:x(x﹣2y)= .三.解答题(共3小题)16.计算:(1)m8•m2.(2)(﹣ab)(a﹣2b2).17.(﹣3y)(4x2y﹣2xy).18.先化简,再求值:(x﹣2y)2﹣x(x+3y)﹣4y2,其中x=﹣4,y=.
单项式乘多项式参考答案与试题解析一.选择题(共10小题)1.【分析】利用单项式乘多项式的运算法则计算得出答案.【解答】解:a2(a﹣2b)=a3﹣2a2b.故选:B.【点评】此题主要考查了整式的运算,正确掌握单项式乘多项式的运算法则是解题的关键.2.【分析】根据整式的除法和乘法、积的乘方、同底数幂的乘法的运算法则解答即可.【解答】解:A、b5÷b3=b2,故这个选项正确;B、(b5)3=b15,故这个选项错误;C、b3•b4=b7,故这个选项错误;D、a(a﹣2b)=a2﹣2ab,故这个选项错误;故选:A.【点评】此题考查了整式的运算,熟练掌握运算法则是解本题的关键.3.【分析】将已知等式左边展开,再比较等式左右两边对应项系数即可.【解答】解:∵x(x2+a)+3x﹣2b=x3+5x+4恒成立,∴x3+(a+3)x﹣2b=x3+5x+4,∴,解得.故选:C.【点评】本题考查了整式混合运算的运用,等式恒成立,等式左右两边对应项系数相等是解题的关键.4.【分析】先分解因式,再将已知的a﹣b=3,b﹣c=﹣2,两式相加得:a﹣c=1,整体代入即可.【解答】解:a2﹣ac﹣b(a﹣c)=a(a﹣c)﹣b(a﹣c)=(a﹣c)(a﹣b),∵a﹣b=3,b﹣c=﹣2,∴a﹣c=1,当a﹣b=3,a﹣c=1时,原式=3×1=3.故选:C.【点评】本题是因式分解的应用,考查了利用因式分解解决求值问题;具体做法是:根据题目的特点,先通过因式分解将式子变形,然后再进行整体代入;但要注意分解因式后,有一个因式a﹣c与已知不符合,因此要对已知的两式进行变形,再代入.5.【分析】由a2﹣2a﹣3=0可得a2﹣2a=3,整体代入到原式=即可得出答案.【解答】解:∵a2﹣2a﹣3=0,∴a2﹣2a=3,则原式===﹣.故选:D.【点评】本题主要考查整式的化简求值,熟练掌握整式的混合运算顺序和法则及代数式的求值是解题的关键.6.【分析】根据单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加计算即可.【解答】解:(﹣3x)•(5x﹣1),=﹣3x•5x+3x•1,=﹣15x2+3x.故选:B.【点评】本题考查了单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.7.【分析】由于x﹣y+3=0,可得x﹣y=﹣3,根据单项式乘多项式、合并同类项和完全平方公式的运算法则将x(x﹣4y)+y(2x+y)变形为(x﹣y)2,再整体代入即可求解.【解答】解:∵x﹣y+3=0,∴x﹣y=﹣3,∴x(x﹣4y)+y(2x+y)=x2﹣4xy+2xy+y2=x2﹣2xy+y2=(x﹣y)2=(﹣3)2=9.故选:A.【点评】考查了单项式乘多项式,单项式与多项式相乘时,应注意以下几个问题:①单项式与多项式相乘实质上是转化为单项式乘以单项式;②用单项式去乘多项式中的每一项时,不能漏乘;③注意确定积的符号.注意整体思想的运用.8.【分析】先利用单项式乘以多项式法则将要求值的多项式进行整理,将题目所给的有确定值的式子进行变形,得出所需要的式子的值,运用整体代入法既可求解.【解答】解:∵m+n=p+q=4,∴(m+n)(p+q)=4×4=16,∵(m+n)(p+q)=mp+mq+np+nq,∴mp+mq+np+nq=16,∵mp+nq=4,∴mq+np=12,∴(m2+n2)pq+mn(p2+q2),=m2pq+n2pq+mnp2+mnq2,=mp•mq+np•nq+mp•np+nq•mq,=mp•mq+mp•np+np•nq+nq•mq,=mp(mq+np)+nq(np+mq),=(mp+nq)(np+mq),=4×12,=48,故选:A.【点评】本题需要综合运用单项式乘以多项式、多项式乘以多项式法则,将式子通过变形后整体代入求解,解题的关键是对条件所给的式子变形要有方向性和目的性,同时要掌握分组分解法对式子进行因式分解,有一定难度.9.【分析】根据单项式乘以单项式,幂的乘方和积的乘方求出m、n的值,再求代数式的值.【解答】解:因为(amb•abn)5=(am+1bn+1)5=a5m+5b5n+5,(amb•abn)5=a10b15,所以5m+5=10,5n+5=15,所以m=1,n=2,所以3m(n2+1)=3×1×(22+1)=15.故选:D.【点评】本题考查了代数式的求值,能够正确的求出m、n的值是解题的关键.10.【分析】根据乘除法的互逆性首先求出B,然后再计算B+A即可求解.【解答】解:由题意,得B÷A=x2+x,所以B=A(x2+x)=2x(x2+x)=2x3+x2,所以B+A=2x3+x2+2x.故选:A.【点评】此题主要考查了整式的乘法以及整式的加法,题目比较基础,基本计算是考试的重点.二.填空题(共5小题)11.【分析】根据负整数指数幂定义进行计算即可.【解答】解:x﹣1(x﹣y)﹣2z=××z=.故答案为:.【点评】本题考查了单项式乘多项式、负整数指数幂,解决本题的关键是掌握负整数指数幂定义.12.【分析】根据单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加计算即可.【解答】解:3a•(2a﹣5)=6a2﹣15a.故答案为:6a2﹣15a.【点评】此题考查了单项式乘多项式,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.13.【分析】根据多项式除以单项式的运算法则计算即可.【解答】解:因为3ab•A=6a2b﹣9ab2,所以A=(6a2b﹣9ab2)÷3ab=2a﹣3b.故答案为:2a﹣3b.【点评】此题主要考查了整式的运算,正确运用多项式除以单项式的运算法则是解题的关键.14.【分析】由题意知,长方形的面积等于长2a乘以宽(a+b),面积也等于四个小图形的面积之和,从而建立两种算法的等量关系.【解答】解:长方形的面积等于:2a(a+b),也等于四个小图形的面积之和:a2+a2+ab+ab=2a2+2ab,即2a(a+b)=2a2+2ab.故答案为:2a(a+b)=2a2+2ab.【点评】本题考查了单项式乘多项式的几何解释,列出面积的两种不同表示方法是解题的关键.15.【分析】根据单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加计算即可.【解答】解:x(x﹣2y)=x2﹣2xy.故答案为:x2﹣2xy.【点评】本题考查了单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意符号的处理.三.解答题(共3小题)16.【分析】(1)根据同底数幂的乘法法则进行计算即可;(2)根据单项式乘以多项式法则进行计算即可.【解答】解:(1)原式=m10;(2)原式=﹣a2b+2ab3.【点评】本题考查了整式的运算,能正确运用法则进行化简是解此题的关键.17.【分析】根据单项式乘多项式的运算法则计算即可.【解答】解:(﹣3y)(4x2y﹣2xy)=(﹣3y)(4x2y)+(﹣3y)(﹣2xy)=﹣12x2y2+6xy2.【点评】此题考查单项式乘多项式,解题的关键是熟练掌握单项式乘多项式的运算法则.18.【分析】根据完全平方公式、单项式乘多项式的法则把原式进行化简,代入已知数据计算即可.【解答】解:原式=x2﹣4xy+4y2﹣x2﹣3xy﹣4y2=﹣7xy,当x=﹣4,y=时,原式=﹣7×(﹣4)×=14.【点评】本题考查的是单项式乘多项式,掌握完全平方公式、单项式乘多项式的法则是解题的关键.
相关课件
这是一份数学七年级下册4 整式的乘法课文配套课件ppt,文件包含142整式的乘法pptx、14整式的乘法第2课时单项式与多项式相乘doc等2份课件配套教学资源,其中PPT共20页, 欢迎下载使用。
这是一份2020-2021学年9.2 单项式乘多项式教学演示课件ppt,共18页。PPT课件主要包含了ab+ac+ad,ab+c+d,根据乘法的分配律,边学边练,牛刀小试,练一练,学以致用练一练,学以致用,思维拓展等内容,欢迎下载使用。
这是一份初中数学北师大版七年级下册4 整式的乘法优秀ppt课件,共22页。PPT课件主要包含了学习目标,导入新课,多项式,多项式的项,指出多项式,讲授新课,mx米,3由此可知,做一做,2原式等内容,欢迎下载使用。











